
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Иваново 2012 4 page
|
|
· принцип последовательной проводки заявок;
· принцип параллельной работы объектов (объектный принцип моделирования).
Принцип Δt
Принцип состоит в том, что алгоритмом моделирования имитируется движение, то есть изменение состояния системы, в фиксированные моменты времени: 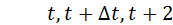 Изменения системы отслеживаются такт за тактом в заданные моменты. Это наиболее универсальный из рассматриваемых принципов, так как применим к очень широкому классу систем. Он же является наиболее простым в реализации.
Изменения системы отслеживаются такт за тактом в заданные моменты. Это наиболее универсальный из рассматриваемых принципов, так как применим к очень широкому классу систем. Он же является наиболее простым в реализации.
Однако это самый неэкономичный принцип, поскольку вся система анализируется моделирующим алгоритмом на каждом такте, даже если в ней не происходит никаких изменений. Кроме того, времена событий округляются до величины Δ t, что ведет к погрешностям в определении переменных, характеризующих систему.
Принцип особых состояний
Назовем состояние, в котором обычно находится система, обычным состоянием. Такие состояния интереса не представляют, хотя занимают большую часть времени.
Особые состояния – это такие состояния в изолированные моменты времени, в которых характеристики системы изменяются скачкообразно. Для изменения состояния системы нужна определенная причина, например, приход очередного входного сигнала. Ясно, что с точки зрения моделирования интерес представляет именно изменение характеристик системы, то есть принцип требует отслеживания моментов перехода системы из одного особого состояния в другое.
Принцип последовательной проводки заявок
Принцип состоит в том, что каждая заявка отслеживается от момента поступления ее в систему до момента ее выхода из системы. И только потом рассматривается следующая заявка.
Объектный принцип моделирования
Как правило, алгоритмы, спроектированные по первым трем принципам, плохо модернизируются. А производственная ситуация часто меняется и требует соответствующих моделей для нахождения рациональных решений в процессе управления.
Таким образом, возникла необходимость в приемах моделирования, обеспечивающих независимость составления моделей элементов сложной системы от изменения задачи или структуры производства. Такой подход моделирования отдельных объектов независимо друг от друга позволяет собирать сколь угодно сложные системы без изменения их составляющих. Принцип объектного моделирования обеспечивает модернизацию сложных систем, удлиняя жизненный цикл АСУ.
марковские цепи
потоки с последействием
Теорема Бернулли:
при неограниченном увеличении числа опытов n частота события A сходится по вероятности к его вероятности P:
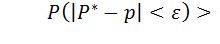 .
.
ЗАДАНИЯ
1. Моделирование простейшей системы
А. Используя имитационный алгоритмический способ составить модель для задачи с человеком и автобусом, если человек идёт в ту же сторону, что и автобус. Учесть, что Ваши объекты могут никогда не встретиться при каких-то начальных условиях.
Пункты «Б» и «В» – по вариантам:
| Б. Усложнить задачу | В. Сделать возникающие препятствия статистическими | |
| Поставить на пути автобуса остановки на 5 минут через каждые x км | Длительность остановок – от 0 до 5 минут | |
| Поставить на пути человека ларёк, у которого он задержится на 5 минут | Время на покупку – от 0 до 10 минут | |
| Устроить на пути автобуса ремонт дороги, где ему придется снизить скорость до 5 км/час | Длина ремонтируемого участка – от 0 до 10 км | |
| Человек, уставая, уменьшает скорость на 10% после каждых 30 минут бега | Человечек нервный, каждые 30 мин то увеличивает, то уменьшает скорость, которая может быть от 3 до 8 км/час | |
| Поставить на пути автобуса шлагбаум, который закрывается через каждые 20 минут на 5 минут | Шлагбаум может оказаться и закрытым, и открытым (вероятность закрытости 25%). Если он закрыт, то откроется через 0-10 минут | |
| Устроить человеку увеличение скорости на 2 км/час через X км после его выхода | Увеличение скорости – от 1 до 50%, место ускорения – от 0,5 до 1,5 км от дома |
Чтобы использовать датчик случайных чисел, в программе надо использовать Randomize. Функция RND возвращает случайные значения в диапазоне [0; 1[ (ноль возможен, единица – нет). Если нужны целые случайные числа от 3 до 20, например, используйте Sl=Int((20-3)*Rnd+3)
2.Статическая регрессионная модель
Создать линейную одномерную регрессионную модель чёрного ящика, если экспериментальные значения на входе (X) и на выходе (Y) представлены в таблице 1.
| Варианты 1, 2, 3 | Варианты 4, 5, 6 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| X | Y | X | Y | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Вар. 1 | Вар. 2 | Вар. 3 | Вар. 4 | Вар. 5 | Вар. 6 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
Найти коэффициенты, среднеквадратичное отклонение, относительное количество точек, попадающих в полосу шириной 2σ. Определить и объяснить, можно ли использовать линейную регрессионную модель.
3.Динамическая регрессионная модель
Суть задания – коллективно разработать программу, определяющую динамическую регрессионную модель для звена 2 порядка[9].
Предполагается, что для проверки работы программы будет задан набор значений 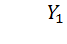 являющийся табличным представлением некоторой функции Y(t) – решения дифференциального уравнения 2 порядка
являющийся табличным представлением некоторой функции Y(t) – решения дифференциального уравнения 2 порядка
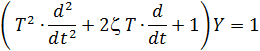
с заданными постоянными  и
и  . Для имитации экспериментальных результатов, к полученным значениям Y добавляется "погрешность измерений" – случайная добавка.
. Для имитации экспериментальных результатов, к полученным значениям Y добавляется "погрешность измерений" – случайная добавка.
Вариант №1. Обеспечение тестового задания и разработка интерфейса общей программы (считывание данных и вывод результатов в числовом и графическом виде).
Вариант №2. Формирование матрицы и столбца свободных членов для динамической регрессионной модели 2 порядка со входным сигналов в виде функции Хэвисайда (см. уравнение (3) и обозначения (4)).
Вариант №3. Реализация метода Крамера решения систем линейных уравнений 3 порядка.
Вариант №4. С оздание процедуры, реализующей аналитическое решение линейного дифференциального уравнения второго порядка с постоянными коэффициентами и постоянной правой частью. Обратить внимание, что решения различны в зависимости от значений коэффициентов уравнения (см. приложение 1).
Вариант №5. Построение имитации поведения системы по определенной ранее модели (т.е. с использованием найденных ранее коэффициентов).
4.Метод Монте-Карло и генераторы случайных чисел
А. Методом Монте-Карло определить
1) значение интеграла
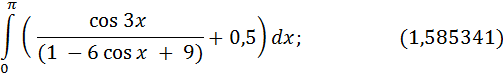
2) вероятность выпадения комбинации 5-6 на двух игральных костях; ( 0,055)
0,055)
3) вероятность вытащить из колоды (36 карт) подряд три карты одной масти; (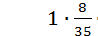 0,047)
0,047)
4) вероятность выбросить тройку (три одинаковых камня или больше) на пяти игральных костях;
(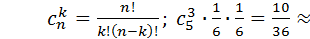 )
)
5) значение интеграла

6) вероятность получить 2-х тузов (ровно) при сдаче в преферансе (32 карты от 7 до туза, сдается по 10 карт). ( =0,048)
=0,048)
Б. Параллельно с решением поставленной задачи проверить используемый ГСЧ на
· равномерность распределения (рассчитать, математическое ожидание, дисперсию, среднеквадратичное отклонение, провести частотный тест и проверку по критерию  );
);
· статистическую независимость.
5.Моделирование СМО
1. Необходимо выбрать некую систему массового обслуживания и создать ее модель, используя один из четырех основных принципов регламентации событий (принцип  , принцип особых состояний, принцип последовательной проводки заявок или принцип параллельной работы объектов). Обосновать выбор принципа построения алгоритма.
, принцип особых состояний, принцип последовательной проводки заявок или принцип параллельной работы объектов). Обосновать выбор принципа построения алгоритма.
2. Исследовать систему с помощью созданной модели, представить результаты в виде статистически обработанных данных. Сделать выводы о работе системы.
3. Рассмотреть, к каким результатам приведет изменение параметров системы.
4. Оценить точность статических характеристик.
Пример моделирования системы массового обслуживания с использованием принципа последовательной проводки заявок можно найти в приложении 4.
Date: 2015-07-17; view: 383; Нарушение авторских прав