
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Иваново 2012 1 page
|
|
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ
Федеральное государственное бюджетное образовательное учреждение
высшего профессионального образования
«ИВАНОВСКАЯ ГОСУДАРСТВЕННАЯ ТЕКСТИЛЬНАЯ АКАДЕМИЯ»
(ИГТА)
Кафедра ПМИТ
Моделирование процессов и систем
Методические указания
для бакалавров по направлению подготовки 230400
«Информационные системы и технологии»
Иваново 2012
Методические указания предназначены для бакалавров по направлению подготовки 230400 – "Информационные системы и технологии". Методические указания представляют собой изложение теоретического материала по дисциплине «Моделирование процессов и систем» и набор заданий для лабораторных работ.
В методических указаниях учтены требования федерального государственного образовательного стандарта высшего профессионального образования по указанному направлению подготовки.
Составитель канд. физ.-мат. наук, доц. Е.А. Кухтина
Научный редактор д-р техн. наук, проф. Н.А. Коробов
ОСНОВНЫЕ ПОНЯТИЯ ТЕОРИИ МОДЕЛИРОВАНИЯ
Моделирование как метод научного познания
Основным методом научных исследований является эксперимент с изучаемым объектом, явлением или процессом. Под экспериментом понимают научную постановку опытов и наблюдение за поведением исследуемой системы. Но зачастую он может быть трудновыполним или просто невозможен. Именно в этих случаях применяют особую форму эксперимента, называемую моделированием. Не стóит устраивать ядерную катастрофу, чтобы выяснить масштабы возможного заражения, но с помощью компьютерной модели возможен достаточно точный расчет интересующих исследователей параметров.
Моделирование в научных исследованиях стало применяться еще в глубокой древности и постепенно захватывало все новые области научных знаний. В настоящее время проблемы составления и исследования моделей различных систем занимают одно из видных мест современной науки, а стремительно возрастающие возможности вычислительной техники обеспечивают успех этому научному направлению.
Понятие модели и моделирования
Слово «модель» (от лат. modelium) означает «мера», «способ», «сходство с какой-то вещью». Термин «модель» широко используется в различных сферах человеческой деятельности и имеет множество смысловых значений. В рамках курса под «моделью» подразумевается некий материальный или мысленно представляемый объект, который в процессе исследования замещает объект-оригинал так, что его непосредственное изучение дает новые знания об объекте-оригинале.
Модель – это искусственно созданный объект, дающий упрощенное представление о реальном объекте, процессе или явлении, отражающий существенные стороны изучаемого объекта с точки зрения цели моделирования. Модель – результат отображения одной структуры на другую.
Объект, для которого создается модель, называют оригиналом или прототипом. Любая модель не является абсолютной копией своего оригинала, она лишь отражает некоторые его качества и свойства, наиболее существенные для выбранной цели исследования. Так, моделью Земли на уроках географии является глобус, но при рассмотрении движения планет Землю представляют материальной точкой. При создании модели всегда присутствуют определенные допущения и гипотезы.
Моделирование – это способ, приём познания, позволяющий с помощью одной системы, чаще всего искусственной, воспроизвести в необходимом объёме и с достаточной точностью исследуемые свойства более сложной системы, являющейся объектом исследования. Под моделированиемпонимается процесс построения, изучения и применения моделей.
Главная особенность моделирования состоит в том, что это метод опосредованного познания с помощью объектов-заместителей. Модель выступает как своеобразный инструмент познания, который исследователь ставит между собой и объектом и с помощью которого изучает интересующий его объект.
Системный подход к моделированию позволяет создавать полноценные модели. Его особенности заключаются в следующем:
· изучаемый объект рассматривается как система, описание и исследование элементов которой не выступает как цель, а выполняется с учетом поставленной задачи;
· объект не отделяется от условий его существования и функционирования и рассматривается как составная часть чего-то целого;
· один и тот же исследуемый элемент рассматривается как обладающий разными характеристиками, функциями и даже принципами построения;
· допускается возможность наличия у объекта множества индивидуальных характеристик и степеней свободы;
· учитываются не только причинные объяснения функционирования объекта, но и целесообразность включения его в состав других элементов, альтернативы решения задач сравниваются в первую очередь по критерию "стоимость-эффективность".
Создание универсальных моделей – это следствие использования системного подхода.
В информатике моделирование называют вычислительным экспериментом, и основывается он на трех основных понятиях: модель – алгоритм – программа.
Понятие информационной модели
Можно конструировать реальные модели объекта, такие как глобус или макет здания. Однако моделирование возможно и путем описания свойств исследуемого объекта без создания его физического прототипа. Это идеальное моделирование, использующее теоретический метод познания. По-другому его называют, абстрактным, нематериальным. Абстрактные модели можно разделить на воображаемые и информационные.
Информационная модель – это совокупность информации об объекте, описывающая свойства и состояние объекта, процесса или явления, а также связи и отношения с окружающим миром.
Информационные модели представляют объекты в виде словесных описаний, текстов, рисунков, таблиц, схем, чертежей, формул и т.д. Информационная модель строится на информации, является системой информации и выражается на языке описания (знаковое моделирование) или языке представления (образно-знаковое или образное моделирование).
Виды моделирования
Принято различать несколько видов моделирования (рис. 1):
| Рис. 1. Виды моделирования |
| Моделирование |
| Реальное (физическое) |
| Идеальное (мысленное) |
| образное (наглядное) |
| Знаковое (символическое) (образное) |
| Образно-знаковое |
| рисунки фотографии иконки кинофильмы графика… |
| схемы графики карты чертежи таблицы… |
| ноты языки фонемы … |
| математическое моделирование |
Физическое (реальное) моделирование – это замена исследуемого объекта материальным. При этом модель воспроизводит свойства, строение, действия объекта-оригинала (кукла – модель внешнего вида человека, робот – модель действий человека).
Мысленное (идеальное) моделирование – замена исследуемого объекта абстрактным (системой информации). Идеальную модель нельзя потрогать, у нее нет материального воплощения.
Наглядное (образное) моделирование – это выражение свойств оригинала с помощью образов.
Образно-знаковое моделирование использует образы определенного вида, дополненные специальными правилами их объединения и преобразования.
Символическое (знаковое) моделирование использует алфавиты разговорных и формальных языков (условные знаки, специальные символы, буквы, цифры) и предусматривает совокупность правил оперирования с этими знаками. Это языковые системы (в частности, языки программирования), физические, химические и математические формулы, нотная запись и т. д.
Математическое и компьютерное моделирование
Одним из важнейших видов знакового моделирования является математическое моделирование – способ представления информационной модели, отображающий связь различных параметров объекта через математические формулы и понятия.
| Рис. 2. Виды математического моделирования |
| Математическое моделирование |
| Аналитическое |
| Компьютерное |
| численное |
| статистическое |
| имитационное |
Для аналитического моделирования характерно то, что процессы функционирования элементов системы записываются в виде некоторых функциональных соотношений (алгебраических, интегральных, дифференциальных, конечно-разностных и т. п.) или логических условий. Аналитическая модель может быть исследована следующими методами: а) аналитическим, когда стремятся получить в общем виде явные зависимости для искомых характеристик; б) численным, когда, не умея решать уравнений в общем виде, стремятся получить числовые результаты при конкретных начальных данных; в) качественным, когда, не имея решения в явном виде, можно найти некоторые свойства решения.
Компьютерная модель – это созданный за счет ресурсов компьютера виртуальный образ, качественно и количественно отражающий внутренние свойства и связи моделируемого объекта или системы, иногда передающий даже внешние характеристики.
При численном моделировании для построения модели используются методы математики, а вычислительный эксперимент заключается в решении математических уравнений численными методами при заданных значениях параметров.
При имитационном моделировании реализующий модель алгоритм воспроизводит процесс функционирования системы во времени, причем имитируются элементарные явления, составляющие процесс, с сохранением их логической структуры и последовательности протекания во времени, что позволяет по исходным данным получить сведения о состояниях процесса в определенные моменты времени, дающие возможность оценить характеристики системы. Основным преимуществом имитационного моделирования по сравнению с моделированием аналитическим является возможность решения более сложных задач.
Метод статистического моделирования используется, если результаты, полученные при воспроизведении на имитационной модели процесса функционирования системы, являются реализациями случайных величин и функций, а для нахождения характеристик процесса требуется его многократное воспроизведение с последующей статистической обработкой.
Все перечисленные виды моделирования не являются взаимоисключающими и могут применяться при исследовании сложных объектов либо одновременно, либо последовательно, либо в некоторой комбинации. Весьма условно также разделение математического моделирования: компьютерное моделирование основано на аналитике, а аналитические модели без компьютерных методов решения уравнений охватят только очень узких класс задач.
Пример моделирования простейшей системы
Сложность задачи часто диктует тот способ представления модели, который будет использоваться при её описании. Рассмотрим простейшую задачу.
Задача. Пусть два объекта (например, автобус и пешеход), находящиеся в начальный момент времени на расстоянии D друг от друга, движутся навстречу со скоростями V 1 и V 2 соответственно. Необходимо узнать: когда и где встретятся эти объекты?
Аналитический явный способ
Эта модель весьма далека от реальности. Идеализация заключается в том, что дорога считается идеально прямой, без уклонов и подъёмов, скорости объектов считаются постоянными, желания объектов не меняются, силы безграничны, отсутствуют помехи для движения, модель не зависит от величин D, V 1, V 2. Что-либо изучить на ней представляется проблематичным, так как из неё можно найти только время и место встречи: T1 =D/(V1+V2)
S1 =V1·T1
Но за счёт большой идеализации получается очень простая модель, которая может быть разрешена в общем виде (аналитически).
Аналитический неявный способ
Получим связь переменных в виде системы уравнений.
T1·(V1 + V2) = D
S1 = V1·T1.
Теперь можно формулировать целый ряд произвольных задач, например так: T1 =? Или так: S2 =?
При этом задачи формулируются пользователем и не предусматриваются специально при моделировании. Это более качественная модель: идеализация её велика, но за счёт неявной формы записи появилась возможность изменения задачи.
Имитационный алгоритмический способ
Процесс берётся не в целом, а по шагам. Время (переменная t) отслеживается счётчиком с шагом h. Идея имитации – продвигать автобус и пешехода на величину V · h на каждом шаге, где h – достаточно малая величина. Повторяя пошагово расчёт в цикле, на каждом этапе работы алгоритма будем имитировать течение процесса. Поскольку мы рассматриваем множество актов движения по отдельности, можно по ходу менять все переменные модели.
Например, если автобус достиг остановки (S1 = Sост), то V = 0 на 2 минуты. Остановка процесса имитации определяется суммой путей, пройденных автобусом и пешеходом навстречу друг другу, и сравнением её с расстоянием D.
| Да |
| T=t+h S1=S1+V1*h S2=S2+V2*h |
| S1+S2>=D |
| Возможно изменение значений при выполнении каких-то условий |
Главное отличие имитационных моделей от аналитических состоит в том, что имитационную модель можно постепенно усложнять, не теряя результативности модели. Усложним задачу, введя в неё дополнительное условие. Представим, что на пути автобуса встретится помеха – шлагбаум, который работает по случайному закону. Если шлагбаум закрыт, а автобус находится менее чем за 5 метров от шлагбаума, то он вынужден остановиться (пешеход, кстати, может шлагбаум и обойти, не теряя скорости, лишь бы жив остался).
Промоделировать случайную работу шлагбаума можно с помощью генератора случайных чисел. В различные моменты времени он будет выдавать случайное число r = 0 или r = 1, это будет означать, что шлагбаум закрыт или, соответственно, открыт.
Поскольку алгоритм использует случайные числа в качестве исходных данных, придётся сделать несколько экспериментов и найти средние значения выходных величин. Результат одного эксперимента случаен и ни о чем не говорит. Среднее значение более информативно. Ещё более информативны сведения о среднем значении и разбросе значений вокруг него (дисперсии).
Обратная задача
С какой скоростью надо бежать человеку, чтобы встретиться с автобусом на остановке, находящейся на расстоянии P от его дома?
Формализация систем и классификация моделей
Некоторые термины системного анализа
Объекты реального мира находятся в постоянном взаимодействии между собой, так или иначе взаимосвязаны друг с другом. Наиболее распространённой формой существования взаимосвязанных и взаимодействующих объектов является система.
Система – совокупность элементов, находящихся в отношениях между собой и образующих определённое целостное единство, направленное на достижение единой цели.
Элемент системы – простейшая неделимая часть системы, т.е. предел членения системы с точки зрения решения конкретных задач в рамках определённой цели;
Подсистема – относительно независимая часть системы, обладающая свойствами системы и имеющая подцель, на достижение которой ориентирована подсистема. Если части системы не обладают такими свойствами, а представляют собой совокупность однородных элементов, то такие части называют компонентами.
Составом системы называют совокупность элементов, компонентов и подсистем.
Для системы характерно наличие связей и отношений между образующими её частями, а также неразрывное единство со средой, во взаимоотношениях с которой система проявляет свою целостность.
Связь – ограничение степени свободы элементов, компонентов и подсистем системы. Совокупность связей между частями системы называют структурой системы.
Связи обеспечивают возникновение и сохранение целостных свойств системы, а также характеризуют строение и функционирование системы – статику и динамику. Чем сильнее связи между элементами системы, тем более целостные свойства она проявляет.
По своему характеру связи характеризуются
- направлением (бывают направленными и ненаправленными);
- силой;
- видом.
По виду связи разделяют на связи подчинения, связи порождения, связи управления, связи безразличия.
Важную роль в процессе управления системами играют обратные связи.
Обратная связь – обратное воздействие управляемого процесса на управляющий объект. Она является основой саморегулирования развития систем. Обратная связь позволяет по выходным параметрам определять входные.
Отображение системы производят путём расчленения её на подсистемы, компоненты, элементы с указанием взаимосвязей разного характера. Одна и та же система может быть представлена разными структурами в зависимости от стадии познания объектов или в зависимости от аспектов её рассмотрения и цели создания.
Поведение системы – процесс её перехода из одних состояний в другие в конкретные моменты времени.
Развитие системы – изменение её во времени для достижения поставленной цели.
Внешняя среда – система более высокого порядка по отношению к рассматриваемой системе (рассматриваемая система является элементом или подсистемой внешней среды). Внешняя среда оказывает воздействие на рассматриваемую систему, меняет ее параметры и свойства, влияет на ее поведение. Однако и система, в свою очередь, оказывает воздействие на внешнюю среду.
Современные научные данные позволяют говорить о мире как о бесконечной системе, находящейся в развитии и на разных стадиях развития и на разном уровне системной подчинённости - иерархии.
Системы реального мира классифицируют
· по происхождению: естественные, искусственные и биологические;
· по степени сложности: простые, сложные и большие (очень сложные);
· по степени взаимодействия с другими системами: открытые и замкнутые[1];
· по характеру функционирования: стохастические и детерминированные;
· по принципу работы: дискретные, непрерывные и дискретно-непрерывные;
· по физической природе: реальные и абстрактные (как правило, системы информации);
· по степени целостности: суммативные и целостные;
· по характеру существования: статические и динамические.
Простые системы – системы, элементы которых точно количественно соизмеримы. Элементы простых систем представляют собой её простейшие неделимые части.
Сложные системы – системы, в которых составляющие их элементы являются, в свою очередь, системами. Для больших систем характерно наличие огромного количества разнородных частей, мощные информационные потоки и самоорганизация.
Понятие простых и сложных систем относительно и применимо в контексте рассматриваемого вопроса[2].
Несоответствие фактического и желаемого состояния системы называют проблемой. Обратной стороной проблемы является цель – желаемое состояние системы, которое нередко не совпадает с фактическим.
Формулирование проблем и соответственно формулирование цели и задач является важнейшим этапом в построении и анализе систем. Важным этапом является процесс определения целей подсистем, подчиняющийся следующим правилам:
· цели системы низшего уровня должны быть подчинены целям систем высшего уровня с учётом динамики развития;
· анализ характера расположения целей в разных областях пространства позволяет определить функциональные требования к системе;
· неопределённость поведения системы ставит требование учёта возможных ситуаций при её формировании в интересах развития;
· достижимость цели зависит от расходов ресурсов на её выполнение.
Для количественного описания достижения цели формируют критерии – оценочные количественные показатели, характеризующие степень достижения цели.
Достижение цели нередко многоаспектно (многогранно) и вследствие этого описывается не одним, а целым набором критериев. К нему предъявляют следующие требования: операционность (должен четко указывать путь к достижению цели и давать возможность количественной или качественной оценки), функциональная полнота (должен описывать все аспекты цели), неизбыточность (критерии не должны дублировать друг друга), детерминированность (каждый критерий должен иметь однозначный смысл и характеризовать определенный аспект цели) и т.д.
Формальная модель объекта.
Модель объекта моделирования (системы S), можно представить в виде множества величин, описывающих процесс функционирования реальной системы:
· совокупность начальных условий (входных воздействий на систему)
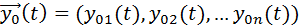 ;
;
· совокупность переменных модели, в которую входят воздействия внешней среды и внутренние параметры системы
 ;
;
· совокупность случайных (стохастических) воздействий на систему
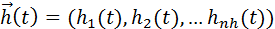 ;
;
· совокупность выходных характеристик системы
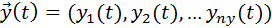 .
.
Входные воздействия  , переменные модели
, переменные модели  и случайные воздействия
и случайные воздействия  являются независимыми (экзогенными) переменными, а выходные характеристики системы
являются независимыми (экзогенными) переменными, а выходные характеристики системы  являются зависимыми (эндогенными) переменными.
являются зависимыми (эндогенными) переменными.
Процесс функционирования системы S описывается во времени законом функционирования системы S:
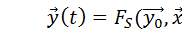 . (1)
. (1)
Соотношение (1) является математическим описанием поведения системы во времени, т. е. отражает её динамические свойства. Поэтому математические модели такого вида принято называть динамическими моделями.
В общем случае закон функционирования системы может быть задан в виде функции, функционала, логических условий, в алгоритмической и табличной формах.
Итак, модель есть зависимость между входными переменными 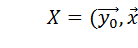 и выходными переменными Y =
и выходными переменными Y =  , т.е. отражает закономерность Y = F (X) и часто является законом. Модель верна в рамках допущенных при её построении гипотез. Поэтому модель ограничена некоторой областью и адекватна в ней.
, т.е. отражает закономерность Y = F (X) и часто является законом. Модель верна в рамках допущенных при её построении гипотез. Поэтому модель ограничена некоторой областью и адекватна в ней.
Если к построенной модели добавить вопрос, то с помощью неё можно решить задачу, получить ответ, который заранее не очевиден (если ответ очевиден, то модель не строят).
модель + вопрос + дополнительные условия = задача.
Условия – любые дополнительные выражения или данные, имеющие смысл ограничений, условий, дополнительных связей. Вопросом может служить одна (или несколько) из неизвестных переменных. Задача доопределяет свободные переменные модели, сужает область возможных решений.
Задачи, решаемые на модели, делятся на прямые (задачи анализа) и обратные (задачи синтеза). Прямые задачи по заданному X находят Y путём подстановки X в уравнение Y = F (X). Обратные задачи по заданному Y находят X путём нахождения обратной функции F –1 и подстановки X = F –1(Y).
Ещё одной специфической задачей является нахождение по заданным X и Y зависимости F или её коэффициентов. Это задача построения модели.
Классификация моделей
В настоящее время модели классифицируют по следующим признакам.
1. По степени полноты модели с точки зрения теории подобия:
а) полное подобие (соответствует полному моделированию как во времени, так и в пространстве);
б) неполное подобие (обращает внимание только на наиболее существенные, характерные параметры исследуемого объекта);
в) приближённое подобие (имеет место приближённое подобие, когда целый ряд показателей не моделируется совсем).
2. По степени учёта исходной информации:
а) детерминированные модели отображают процессы, в которых предполагают отсутствие случайных воздействий  ;
;
б) стохастические модели отображают вероятностные процессы и события (в этом случае анализируются реализации случайных процессов и оцениваются средние характеристики).
3. С точки зрения изменения объекта во времени:
а) статические модели описывают объект в какой-то момент времени и представляют собой отображение между подмножествами свойств моделируемого объекта 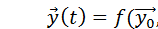 ;
;
б) динамические модели описывают изменение объекта во времени (1).
4. С точки зрения описываемых процессов:
а) дискретные модели отражают описание дискретных систем.
б) непрерывные модели отражают описание непрерывных систем.
в) дискретно-непрерывные модели описывают системы, включающие в себя как непрерывные, так и дискретные компоненты.
Модель называется имитационной, если она предназначена для испытания или изучения, проигрывания возможных путей развития и поведения объекта путем варьирования некоторых или всех параметров. Процесс имитационного моделирования осуществляют с организацией квантования по времени, которое называют системным временем. Величина кванта времени должна быть достаточно мала, чтобы моделируемый процесс был адекватен исследуемому процессу. Y=(Y(t0), Y(t0+Dt), Y(t0+2*Dt),..., Y(t0+L*Dt)), где t0 – начальный момент времени; Dt – шаг квантования по времени; t0+L*Dt – конечный момент времени.
Основные требования к математическим моделям
1. Важнейшим требованием, предъявляемым к математической модели является требование ее адекватности (правильного соответствия) изучаемому реальному объекту. Под адекватностью прежде всего понимается
· правильное качественное описание рассматриваемых свойств объекта;
· правильное количественное описание этих свойств с некоторой разумной точностью.
В соответствии с тем, ставится второе условие или нет, говорят о количественных или качественных моделях. В тех областях, где не выявлено чётких количественных закономерностей (например, в некоторых социальных или биологических науках), математические модели являются, как правило, качественными.
Вместо количественной адекватности говорят также о точности модели. Естественно говорить не просто об адекватности модели, но также о большей или меньшей адекватности. Адекватность следует рассматривать только по определенным признакам – свойствам, принятым в данном исследовании за основные. Всякая адекватность математической модели реальному объекту лишь относительна и имеет свои рамки применимости.
2. Другое требование, предъявляемое к моделям – требование достаточной простоты модели по отношению к исследуемой системе ее свойств. Чрезмерное усложнение модели может привести к громоздким системам уравнений, не поддающимся изучению и решению. Модель считается достаточно простой, если имеющиеся в нашем распоряжении средства исследования дают возможность провести в приемлемые сроки и с приемлемыми затратами, но с разумной точностью анализ исследуемых свойств и осмыслить результат.
Date: 2015-07-17; view: 393; Нарушение авторских прав