
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Иваново 2012 3 page
|
|
Схема статистического эксперимента
| Преобразователь закона случайных чисел |
| Генератор случайных чисел |
| Модель y = φ (x) |
Накопление статистики
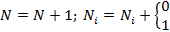
|
Вычисление статистических характеристик: 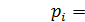
|
| Оценка достоверности |
| Рис. 11. Схема статистического эксперимента |
| Ответ |
Построив модель системы со случайными параметрами, на ее вход подают входные сигналы от генератора случайных чисел. Он устроен так, что выдает равномерно распределенные случайные числа из интервала [0;1]. Так как одни события могут быть более вероятными, другие – менее вероятными, то равномерно распределенные случайные числа от генератора подают на преобразователь закона случайных чисел, который преобразует их в заданный пользователем закон распределения вероятности, например, в нормальный или экспоненциальный закон. Эти преобразованные случайные числа x подают на вход модели.
Модель отрабатывает входной сигнал x по некоторому закону y = φ (x) и получает выходной сигнал y, который также является случайным.
В блоке накопления статистики установлены фильтры и счетчики. Фильтр (некоторое логическое условие) определяет по значению y, реализовалось ли в конкретном опыте некоторое событие (выполнилось или не выполнилось некое условие). Если событие реализовалось, то счетчик события Ni увеличивается на единицу. Если требуется следить за несколькими разными типами событий, то для статистического моделирования понадобится несколько фильтров и счетчиков. Всегда ведется подсчет количества экспериментов N.
Далее отношение Ni к N дает оценку вероятности pi появления события i, то есть указывает на частоту его выпадения в серии из N опытов. Это позволяет сделать выводы о статистических свойствах моделируемого объекта.
Например, событие A совершилось в результате проведенных 200 экспериментов 50 раз. Это означает, что вероятность совершения события равна 0,25. Вероятность того, что событие не совершится, равна, соответственно, 1 – 0,25 = 0,75.
Генераторы случайных чисел
В основе метода Монте-Карло лежит генерация случайных чисел, которые должны быть равномерно распределены в интервале (0;1). Если генератор выдает числа, смещенные в какую-то часть интервала (одни числа выпадают чаще других), то результат решения задачи может оказаться неверным. Поэтому проблема использования генератора действительно случайных и действительно равномерно распределенных чисел стоит очень остро.
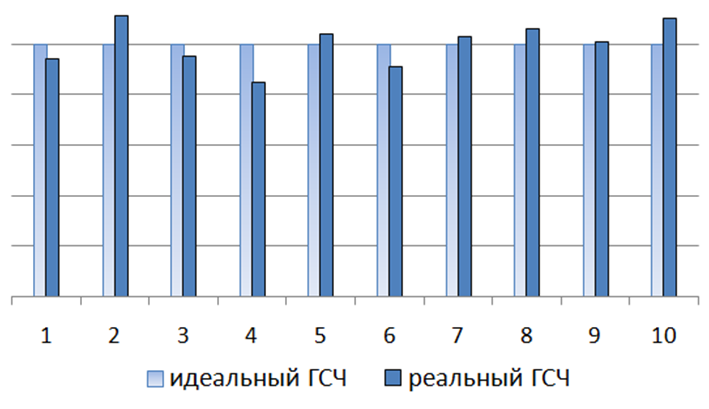
За эталон генератора случайных чисел (ГСЧ) принят такой генератор, который порождает последовательность случайных чисел с равномерным законом распределения. Если наблюдать такой ГСЧ достаточно длительное время, то окажется, что в каждый из десяти, например, интервалов (0;0.1), (0.1;0.2), …, (0.9;1) попадет одинаковое количество случайных чисел (рис. 12).
| Рис. 12. Частотная диаграмма выпадения случайных чисел, порождаемых идеальным и реальным генераторами. |
Генераторы случайных чисел по способу получения чисел делятся
· на физические (монета, игральные кости, рулетка, генератор шума);
· табличные (специальным образом составленные таблицы, содержащие проверенные некоррелированные[8] цифры);
· алгоритмические.
Числа, генерируемые с помощью алгоритмических ГСЧ, всегда являются псевдослучайными, то есть каждое последующее сгенерированное число зависит от предыдущего: 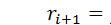 Последовательности, составленные из таких чисел, образуют петли, т.е. обязательно существует цикл (период), повторяющийся бесконечное число раз.
Последовательности, составленные из таких чисел, образуют петли, т.е. обязательно существует цикл (период), повторяющийся бесконечное число раз.
Проверка качества работы генератора
От качества работы ГСЧ зависит качество работы всей системы и точность результатов. Поэтому случайная последовательность, порождаемая ГСЧ, должна удовлетворять целому ряду критериев.
Осуществляемые проверки бывают двух типов:
· проверки на равномерность распределения;
· проверки на статистическую независимость.
Проверки на равномерность распределения
1. ГСЧ должен выдавать близкие к следующим значения статистических параметров, характерных для равномерного случайного закона
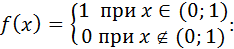
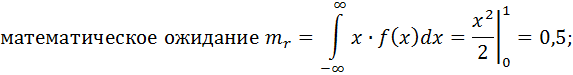
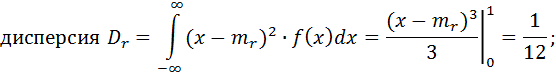
2. Частотный тест
Частотный тест позволяет выяснить, сколько чисел попало в интервал 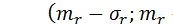 , где
, где 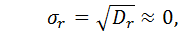 (в хорошем ГСЧ в этот интервал должно попадать около 57,7% всех чисел).
(в хорошем ГСЧ в этот интервал должно попадать около 57,7% всех чисел).
Кроме того, количество чисел, попавших в интервал (0; 0.5), должно быть примерно равно количеству чисел, попавших в интервал (0.5; 1).
3. Проверка по критерию «хи-квадрат» (критерию Пирсона)
Критерий  , предложенный в 1900 году Карлом Пирсоном, является основным критерием, используемым для проверки, удовлетворяет ли рассматриваемая случайная величина заданному закону распределения.
, предложенный в 1900 году Карлом Пирсоном, является основным критерием, используемым для проверки, удовлетворяет ли рассматриваемая случайная величина заданному закону распределения.
Поскольку закон распределения идеального ГСЧ равномерный, и теоретическая вероятность попадания чисел в i -й интервал равна  , то в каждый из k интервалов попадет ровно по
, то в каждый из k интервалов попадет ровно по  чисел, если N – общее количество сгенерированных чисел. При работе реального ГСЧ в каждый интервал попадет
чисел, если N – общее количество сгенерированных чисел. При работе реального ГСЧ в каждый интервал попадет  чисел. Критерий
чисел. Критерий  для экспериментальных данных выражается как
для экспериментальных данных выражается как
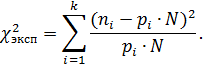
| (12) |
Можно несколько упростить это выражение:
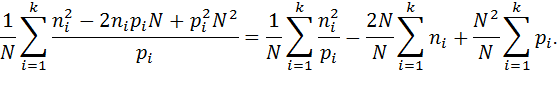
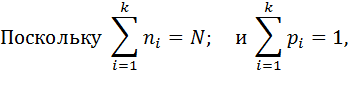
| (13) | ||
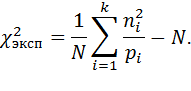
| (14) | ||
Для распределения  составлены специальные таблицы (см. приложение 2). Как видно из таблицы приложения 2, распределение
составлены специальные таблицы (см. приложение 2). Как видно из таблицы приложения 2, распределение  зависит от параметра
зависит от параметра  , называемого числом степеней свободы. Число
, называемого числом степеней свободы. Число  равно количеству разрядов k минус число независимых условий ("связей"), наложенных на частоты. Требование (13), т.е. требование того, чтобы сумма частот была равна единице, накладывается во всех случаях. Если этим набор условий ограничивается, то
равно количеству разрядов k минус число независимых условий ("связей"), наложенных на частоты. Требование (13), т.е. требование того, чтобы сумма частот была равна единице, накладывается во всех случаях. Если этим набор условий ограничивается, то 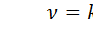
Пользуясь таблицами можно оценить степень согласованности теоретического и статистического распределений. Если случайная величина действительно распределена по закону F (в нашем случае – равномерно), то найденная по таблице вероятность  есть вероятность того, что за счет чисто случайных причин мера расхождения теоретического и статистического (реального) распределений будет не меньше, чем полученное в серии опытов значение
есть вероятность того, что за счет чисто случайных причин мера расхождения теоретического и статистического (реального) распределений будет не меньше, чем полученное в серии опытов значение  . Пример использования найденных значений
. Пример использования найденных значений  и теоретических значений, собранных в таблицах, приведен в приложении 2.
и теоретических значений, собранных в таблицах, приведен в приложении 2.
Итак, процедура проверки имеет следующий вид:
· диапазон от 0 до 1 разбивается на k равных интервалов;
· запускается ГСЧ N раз (N должно быть велико, например, 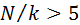 );
);
· определяется количество 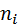 случайных чисел, попавших в каждый интервал (
случайных чисел, попавших в каждый интервал (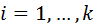 );
);
· вычисляется экспериментальное значение χ2эксп. по формуле (12) или (14);
· путем сравнения экспериментально полученного значения 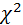 с теоретическим из табл. 1 делается вывод о пригодности генератора для использования.
с теоретическим из табл. 1 делается вывод о пригодности генератора для использования.
Если найденная по таблицам вероятность  мала, то гипотеза о том, что ГСЧ выдает равномерно распределенные числа отбрасывается как неправдоподобная. Если же χ2эксп. очень мало, то разумно признать, что столь близкое совпадение обусловлено не идеальностью генератора, а "неслучайностью" полученных чисел. Есть мнение, что чем ближе
мала, то гипотеза о том, что ГСЧ выдает равномерно распределенные числа отбрасывается как неправдоподобная. Если же χ2эксп. очень мало, то разумно признать, что столь близкое совпадение обусловлено не идеальностью генератора, а "неслучайностью" полученных чисел. Есть мнение, что чем ближе  к значению 50%, тем лучше.
к значению 50%, тем лучше.
Проверки на статистическую независимость
1. Проверка на частоту появления цифры в последовательности.
Случайное число состоит из цифр. Имеет смысл, рассматривая несколько полученных подряд случайных чисел, проверить частоту появления каждой цифры по критерию  .
.
2. Проверка появления серий из одинаковых цифр.
Например, в последовательности «24633899915467766618» есть 2 серии длиной в 2 символа (33 и 77) и 2 серии длиной в 3 символа (999 и 666).
Вероятность  появления серии длиной в L равна
появления серии длиной в L равна  .
.
Частота появления серий проверяется по критерию  с использованием значений
с использованием значений  .
.
Моделирование случайной величины с заданным законом распределения
Основные сведения о законах распределения случайных величин можно найти в приложении 3. Так как законы распределения вероятности событий могут быть различными, приходится превращать равномерный ГСЧ в генератор случайных чисел с заданным законом распределения.
Метод ступенчатой аппроксимации
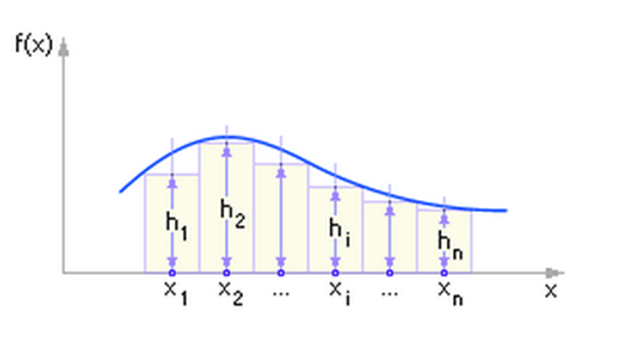
| Рис. 13. Метод ступенчатой аппроксимации |
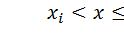 .
.
Операция нормировки обеспечивает равенство единице суммы вероятностей всех n событий: 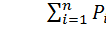 Операцией нормировки значения h переводим в единицы вероятности:
Операцией нормировки значения h переводим в единицы вероятности:
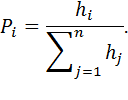
Интервал (0;1) разбивается на n промежутков разной длины (длина i-го промежутка равна  ). Считается, что случайная величина приняла значение
). Считается, что случайная величина приняла значение  , если сгенерированное датчиком число попало в i-й интервал.
, если сгенерированное датчиком число попало в i-й интервал.
Необходимо отметить, метод огрубляет изначальную постановку задачи, т.к. внутри каждого интервала значения x неразличимы.
Метод усечения
| Рис. 14. Метод усечения |
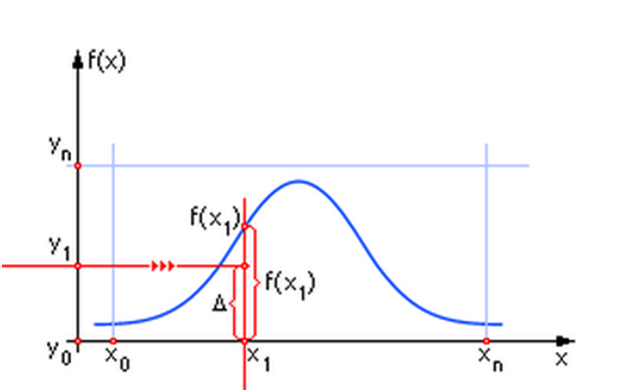 Метод используется в случае, когда функция задана аналитически (в виде формулы). График функции вписывают в прямоугольник (см. рис. 14) На оси X и Y подают случайные равномерно распределенные числа в диапазонах
Метод используется в случае, когда функция задана аналитически (в виде формулы). График функции вписывают в прямоугольник (см. рис. 14) На оси X и Y подают случайные равномерно распределенные числа в диапазонах  и
и  , соответственно.
, соответственно.
Если точка в пересечении этих двух координат лежит ниже кривой плотности вероятности, то событие X произошло, иначе нет.
Моделирование нормально распределенных случайных величин
Естественно, при моделировании нормально распределенной случайной величины можно воспользоваться общими методами (методом усечения, например). Но для нормального закона разработаны отдельные эффективные методы моделирования.
1. Использование центральной предельной теоремы.
Общая идея метода следующая: требуется сложить случайные числа с любым законом распределения, нормализовать их и перевести в нужный диапазон нормального распределения.
Допустим, надо получить ряд случайных чисел x, распределенных по нормальному закону с математическим ожиданием mx и среднеквадратичным отклонением σx.
А. Сложим n случайных чисел, используя стандартный ГСЧ:
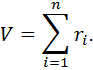
Согласно центральной предельной теореме числа V образуют ряд значений, распределенный по нормальному закону. Эти числа тем лучше описывают нормальный закон, чем больше параметр n (на практике n берут равными 6 или 12). Закон распределения чисел V имеет математическое ожидание 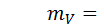

Поэтому он является смещенным относительно заданного произвольного.
Б. С помощью формулы 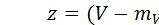 нормализуем этот ряд. Получим нормализованный закон нормального распределения чисел Z.
нормализуем этот ряд. Получим нормализованный закон нормального распределения чисел Z.
В. Формулой 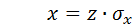 (сдвиг на mx и масштабирование на σx) преобразуем ряд Z в ряд x.
(сдвиг на mx и масштабирование на σx) преобразуем ряд Z в ряд x.
2. Метод Мюллера
Совсем простым методом получения нормальных чисел является метод Мюллера, использующий формулы:
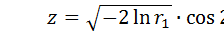 или
или 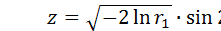 где r 1 и r 2 – равномерно распределенные случайные числа из диапазона [0;1].
где r 1 и r 2 – равномерно распределенные случайные числа из диапазона [0;1].
Моделирование системы случайных величин
Случайные величины X и Y называются независимыми, если закон распределения каждой из них не зависит от того, какое значение приняла другая величина.
Степень зависимости одной случайной величины от другой может характеризовать так называемый коэффициент корреляции  который определяет степень тесноты линейной зависимости между величинами (см. рис. 15).
который определяет степень тесноты линейной зависимости между величинами (см. рис. 15).
Если X и Y связаны функционально (одному значению X соответствует одно определенное значение Y, т.е. Y=aX+b), то 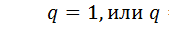 (в зависимости от знака a). Если же X и Y связаны вероятностной зависимостью (зависимость веса человека от его роста, например), то
(в зависимости от знака a). Если же X и Y связаны вероятностной зависимостью (зависимость веса человека от его роста, например), то 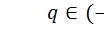 , причем в случае независимых случайных величин
, причем в случае независимых случайных величин 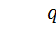
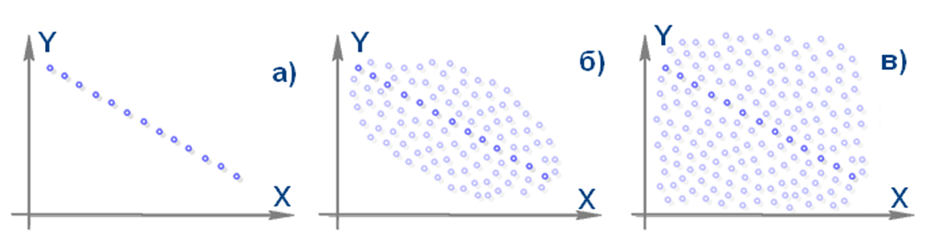
Рис. 15. Зависимость двух случайных величин:
а)  ; б) ; б)  в) в) 
|
Алгоритм моделирования двух зависимых случайных событий
Пусть X и Y распределены по нормальному закону с определенными значениями mx, σx и my, σy. Задан коэффициент корреляции двух случайных событий  , т.е. Y не совсем случайно.
, т.е. Y не совсем случайно.
Тогда возможный алгоритм реализации модели будет следующим.
1. Разыгрывается шесть случайных равномерно распределенных на интервале [0;1] чисел; находится их сумма S. Находится нормально распределенное случайное число x по следующей формуле: 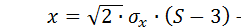
2. По формуле 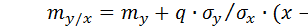 находится математическое ожидание my / x (знак y / x означает, что y будет принимать случайные значения с учетом условия, что x уже принял какие-то определенные значения).
находится математическое ожидание my / x (знак y / x означает, что y будет принимать случайные значения с учетом условия, что x уже принял какие-то определенные значения).
3. По формуле 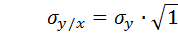 находится среднеквадратическое отклонение σy / x .
находится среднеквадратическое отклонение σy / x .
4. Разыгрывается шесть случайных равномерно распределенных на интервале [0;1] чисел и находится их сумма k. Находится нормально распределенное случайное число y по формуле: 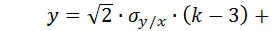 .
.
Потоки случайных событий
Когда похожих друг на друга событий много и они следуют друг за другом, то они образуют поток.
Поток событий – это последовательность однородных событий, наступающих одно за другим в случайные промежутки времени. При этом считается, что статистическая характеристика этого явления (интенсивность потока событий) задана.
Интенсивность потока  – это среднее число событий в единицу времени.
– это среднее число событий в единицу времени.
Поток называют
· детерминированным, если интервал между событиями равен константе или определен какой-либо формулой;
· случайным, если интервал между событиями – случайная величина;
· ординарным, если вероятность одновременного появления двух и более событий равна нулю;
· стационарным, если вероятность попадания того или иного числа событий на участок времени длиной t зависит только от длины участка и не зависит от того, где именно на оси времени он находится, т.е. 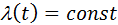 ;
;
· потоком без последействия, если вероятность появления случайного события не зависит от момента совершения предыдущих событий.
Если случайный поток ординарен и не имеет последействия, то его называют пуассоновским потоком. Название "пуассоновский" связано с тем, что при таком потоке число событий, попадающих на любой фиксированный интервал времени, будет распределено по закону Пуассона, т.е. вероятность Pm  того, что за интервал времени
того, что за интервал времени 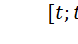 произойдет m событий:
произойдет m событий:
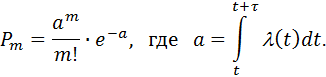
Стационарный пуассоновский поток считают простейшим, для него
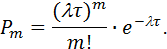
| (15) |
Вероятность P0 "непоявления" события выразится как  если m=0 подставить в формулу (15), а вероятность
если m=0 подставить в формулу (15), а вероятность  появления хотя бы одного события:
появления хотя бы одного события: 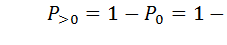
Важной характеристикой потока является закон распределения длины промежутка между соседними событиями. Пусть T – промежуток времени между двумя соседними событиями в простейшем потоке. Хотелось бы найти F(t) – функцию распределения случайной величины T, т.е. вероятность того, что T<t. Рассмотрим обратную величину 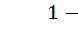 , которая является вероятностью того, что T>t или того, что за время T событие не произойдет:
, которая является вероятностью того, что T>t или того, что за время T событие не произойдет: 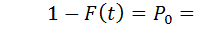 Значит,
Значит, 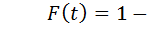 следовательно,
следовательно,
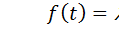 . .
| (16) |
Закон распределения с плотностью (16) называется показательным законом.
Моделирование простейшего потока
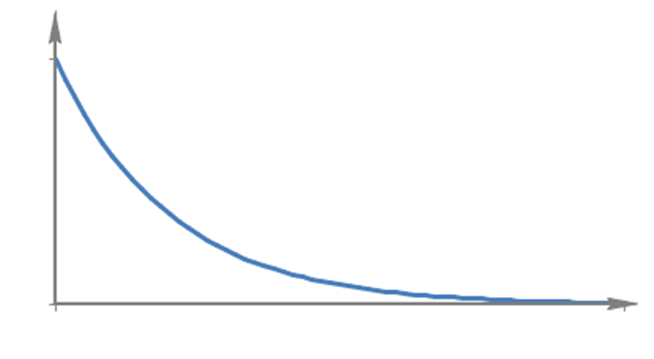
Считаем, что интенсивность потока  задана, и ставим задачу смоделировать возникновение событий через временные интервалы, распределенные по закону (16). Воспользуемся методом ступенчатой аппроксимации (рис. 16), считая, что после некоторого tmax значения f(t) пренебрежимо малы.
задана, и ставим задачу смоделировать возникновение событий через временные интервалы, распределенные по закону (16). Воспользуемся методом ступенчатой аппроксимации (рис. 16), считая, что после некоторого tmax значения f(t) пренебрежимо малы.
| Dt |
| t |
| f(t) |
| tmax |
| hi |
| Рис. 16. Моделирование случайного интервала |
Разбиваем интервал (0; tmax) на n интервалов длиной Dt, а интервал (0;1), в который попадают случайные числа, на n интервалов, длина каждого из которых определяется как  Но
Но 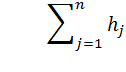 т.к.
т.к.
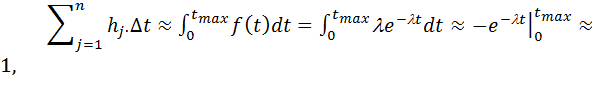
если считать 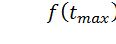 Кроме того,
Кроме того, 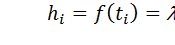 значит,
значит,
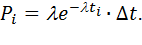
Получая от ГСЧ число r, находим интервал между событиями t, выяснив, в какой по счету интервал попадает r.
Если
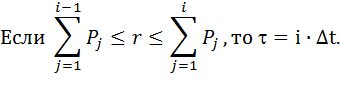
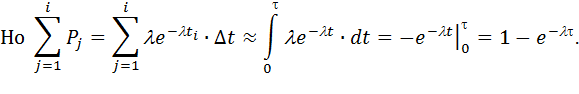
А если 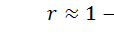 , то
, то 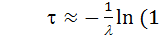 Поскольку
Поскольку  - равномерно распределенное случайное число, то очевидно, что с тем же успехом можно считать
- равномерно распределенное случайное число, то очевидно, что с тем же успехом можно считать 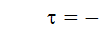
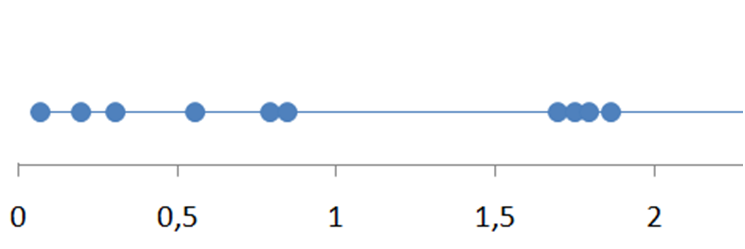
Рис. 17. Поток событий с интенсивностью  . .
|
Потоки с последействием
Системы массового обслуживания (СМО)
Большой класс систем, хорошо изучающихся методами статистического моделирования, но которые сложно изучить аналитическими способами, сводится к системам массового обслуживания (СМО).
В СМО подразумевается, что есть каналы обслуживания, через которые в процессе обработки проходят заявки ( заявки обслуживаются каналами). Каналы могут быть разными по назначению, характеристикам, они могут сочетаться в разных комбинациях; заявки могут находиться в очередях и ожидать обслуживания. Часть заявок может быть обслужена каналами, а части могут отказать в этом. Важно, что заявки, с точки зрения системы, абстрактны: это то, что желает обслужиться, то есть пройти определенный путь в системе. Каналы являются также абстракцией – это то, что обслуживает заявки.
Каналы бывают горячие (начинают обслуживать заявку в момент ее поступления в канал) и холодные (каналу для начала обслуживания требуется время на подготовку). Заявки возникают в случайные моменты времени, согласно какому-то статистическому закону. Заявки, они же клиенты, входят в систему, обслуживаются, покидают систему или обслуженными или неудовлетворенными. Бывают нетерпеливые заявки, они покидают систему по своей воле. Заявки образуют потоки: поток заявок на входе системы, поток обслуженных заявок, поток отказанных заявок. Поток характеризуется количеством заявок определенного сорта, наблюдаемым в некотором месте СМО за единицу времени (час, сутки, месяц), то есть поток есть величина статистическая.
Очереди характеризуются правилами стояния в очереди (дисциплиной обслуживания), количеством мест в очереди (сколько клиентов максимум может находиться в очереди), структурой очереди (связь между местами в очереди). Бывают ограниченные и неограниченные очереди. Наиболее часто встречающиеся дисциплины обслуживания:
· FIFO (First In, First Out – первым пришел, первым ушел): если заявка первой пришла в очередь, то она первой уйдет на обслуживание;
· LIFO (Last In, First Out – последним пришел, первым ушел): если заявка последней пришла в очередь, то она первой уйдет на обслуживание (патроны в рожке автомата);
· SF (Short Forward – короткие вперед): в первую очередь обслуживаются те заявки из очереди, которые имеют меньшее время обслуживания.
Специалист по системам должен хорошо понимать ресурсы производительности и эффективности проектируемых им систем, скрытые в оптимизации параметров, структур и дисциплинах обслуживания. Моделирование помогает выявить эти скрытые резервы.
При анализе результатов моделирования важно также указать интересы и степень их выполнения. Различают интересы клиента и интересы владельца системы. Заметим, что эти интересы совпадают не всегда.
Судить о результатах работы СМО можно по показателям. Наиболее популярные из них:
· вероятность обслуживания клиента системой;
· пропускная способность системы;
· вероятность отказа клиенту в обслуживании;
· вероятность занятости каждого из канала и всех вместе;
· среднее время занятости каждого канала;
· вероятность занятости всех каналов;
· среднее количество занятых каналов;
· вероятность простоя каждого канала;
· вероятность простоя всей системы;
· среднее количество заявок, стоящих в очереди;
· среднее время ожидания заявки в очереди;
· среднее время обслуживания заявки;
· среднее время нахождения заявки в системе.
Принципы компьютерного моделирования СМО
Основная проблема при составлении алгоритмов на машине с последовательной обработкой процессов состоит в том, что при моделировании необходимо отслеживать множество процессов, которые в реальном времени происходят параллельно. В связи с этим алгоритмы моделирования имеют свои особенности:
· продвижение системы во времени, отслеживание временной координаты;
· обеспечение синхронной работы объектов, из которых состоит моделируемая система.
В настоящий момент известны четыре основных принципа регламентации событий.
· принцип 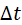 ;
;
· принцип особых состояний;
Date: 2015-07-17; view: 506; Нарушение авторских прав