Оптимизация структуры оборудования, образующего электрическое хозяйство

Рассмотрим подход, изложенный в § 2.4, предложив модель, ко­торая существенно повышает эффективность. В частности, теоретиче­ское значение роста производительности труда при воздействии на

структуру составляет 25-30% при практически легко реализуемом 10-12%. Ключевыми понятиями теории являются: техноценоз, ис­следуемое семейство изделий, элемент-особь, вид, каста, ранговое и видовое Н-распределение.

Применительно к электрическим машинам будем считать одним ви­дом электрическую машину, имеющую совпадающие количественную и качественную характеристики: максимальную мощность и наимено­вание серии (типа), например вид 28А. В этом случае двигатели А71-2, А72-4, А81-6, А82-8 будут одного вида. Для трансформатора вид -ТМ-1000. Каждый элемент ценоза помечается парой чисел: номером и = 1, 2,..., U, где U — число элементов-особей одного семейства, обра­зующих перечень особей — текст Т, и номером вида s =1,2,..., S, где 5 — число видов, образующих словарь объемом V. Особи одного ви­да образуют популяцию. Виды, каждый из которых представлен рав­ным количеством особей, образуют касты, т. е. касту-множество, образованную популяциями одинаковой численности.

Распределение видов - это распределение популяций по кастам. Однозначно описывая соотношения количества видов и численность каждого вида, оно служит теоретической основой предполагаемого подхода. Устойчивость видового распределения дала возможность сделать вывод о действии закона информационного отбора и его объективности. Некоторое идеальное видовое распределение будем называть гиперболическим Н-распределением.

Классификация перечня особей текста Т по видам позволяет соста­вить таблицу рангового распределения, где виды располагаются в порядке уменьшения численности их популяций. В табл. 16.5 приве­дено ранговое распределение Л (г) на примере электродвигателей:

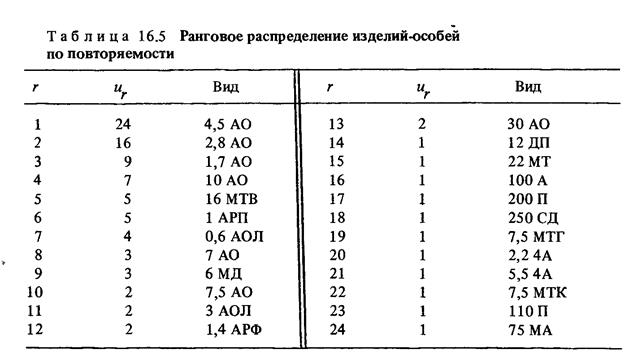
и_r — количество особей вида s_f, соответствующее рангу г. Ранг ви­да s_r есть порядковый номер (номер строки). Последний номер S определяет объем словаря V; можно записать F= \S\. Ранговое распределение выражается в виде зависимости

где 3 > О, В > 0 — константы рангового распределения. Очевидно, что длина текста Т = 2 u_f и объем словаря V = 2s.

Выражение (16.4), известное как закон Ципфа, применимо при исследовании электрических ценозов для удельных и общих расходов электроэнергии, распределения предприятий по максимуму нагруз­ки, количеству электродвигателей и т. д. Ранговое распределение пре­образуется в видовое, которое, как правило, позволяет сделать боль­ше содержательных выводов и служит основой модели управления структурой установленного оборудования.

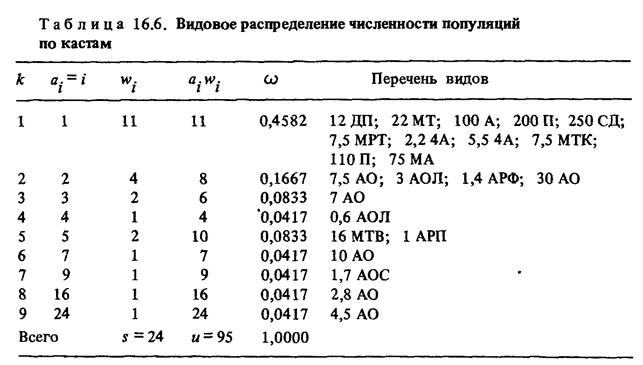
Таблица видового распределения может быть получена из текста Т непосредственно, если выбрать вначале все популяции, состоящие из одной особи а\ = 1; они образуют первую касту k~\, общее число ви­дов в которой w, = 11 (табл. 16.6), численность особей в касте ai\Vi = = 11. Затем выбирают все виды, представленные двумя особями: k = - 1, а_г - 1, и>₂ = 4, a₂W2 = 8; затем — тремя и т. д. Последователь­ность w. называется эмпирическим видовым распределением J2(w.). Число строк в табл. 16.6 равно числу каст k. Обозначим через Л са­мую мощную популяцию.

Запишем на основе табл. 16.6 очевидные соотношения для объема словаря

S(U), £1(Х). Непрерывная кривая распределения, используемая в качестве аппроксимирующей зависимости при обработке эмпирических распределений (рис. 16.2),

где X e [ 1, °°) — непрерывный аналог мощности популяции i; а >0 — постоянная распределения (характеристический показатель); W₀ = AS, где

Date: 2015-06-11; view: 610; Нарушение авторских прав