
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Полюс маневрирования и его свойства
Допустим (рис. 1), что мы имеем два корабля, уравнитель и маневрирующий, которые находились в начальный момент в точках (K0) и (M0) и, спустя некоторый малый промежуток времени (Dt), переместились соответственно в точки (K1) и (M1). По малости промежутка времени (Dt) будем считать вектора перемещений кораблей равными пройденным ими путям:
 |
пустим, что прямые (K0M0) и (K1M1), изображающие пеленги c уравнителя на маневрирующий в начале и в конце промежутка времени (Dt), пересекаются в точке (C).
Рис.1.
Проведем через точки (K0, K1 и C) и точки (M0, M1 и C) окружности, которые, как видно из рисунка, будут иметь кроме точки (C) вторую точку пересечения (P). Назовем эту точку (P) полюсом маневрирования и покажем некоторые основные зависимости, которые связывают маневрирование кораблем с той точкой.
Эта точка обладает рядом особых свойств, заставляющих нас остановиться на них специально. Основные из этих свойств, имеющие место при любом маневрировании двух кораблей относительно друг друга, независимо от способа маневрирования, изложены в виде пяти нижеследующих теорем.[1[КВВ1] ]
Теорема 1. При маневрировании двух кораблей относительно друг друга их курсовые угла на полюс маневрирования одинаковы и равны относительному курсовому углу.
Соединим полюс (P) прямыми с точками (M0, M1, K0, K1 и С).
Угол (K1K0P), являющийся курсовым углом уравнителя на полюс, обозначим (jк), а угол (M1M0P) - курсовой угол маневрирующего на полюс - значком (jм).
Углы (K1CP) и (K1K0P= jк) вписаны в одну и ту же окружность (K0K1CP) и опираются на взаимодополняющие друг друга дуги
(ÈK1K0P=360 - ÈPCK1). Отсюда следует, что:
jк=Ð K1K0P = 1800 - Ð K 1CP
Углы (M1CP) и (M1M0P= jк) также вписаны в одну и ту же окружность (M0M1CP) и также опираются на взаимодополняющие друг друга дуги (ÈM1M0P= 3600 - ÈM1CP), откуда
jк=Ð M1M0P= 1800 - ÐM1CP
Но так как
Ð K 1CP = ÐM1CP
то и
1800 - Ð K 1CP = 1800 - ÐM1CP
откуда jк = jм
Итак, первая часть теоремы доказана. Остается доказать, что
jк = jм = qp
Из треугольника (K1PK0) мы можем написать, что

Нетрудно заметить, что
Ð K1P K0 = Ð K 1C K0 = q
и, следовательно,
|

Рассматривая (PK0) как начальное расстояние от уравнителя до полюса, а (PK1) как конечное расстояние между ними, и обозначив эти расстояния соответственно значками (rk0) и (rk1), а изменение расстояния от уравнителя до полюса за промежуток времени (Dt) значком (D r k), мы можем написать, что
PK1 - PK0 = rk1 - rk0 = D r k
|
D r k = -SK× Сos jк
откуда
|

Разделив выражение (1.2) на выражение (1.3) и заменив в первом из них (PK1) через (rk1), получаем:
|
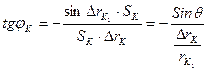
Однако (q) есть не что иное, как изменение пеленга между кораблями за промежуток времени (Dt) и на основании теоремы синусов из треугольника позиций М0К0М1 можно написать:
|

Обратимся к треугольникам (K0PM0) и (K1PM1). У этих треугольников: K0M0P=K1M1P, как вписанные в одну и ту же окружность (M0M1CP) и опирающиеся на одну и ту же дугу (CP).
ÐM0K0P=ÐM1K1P, так как дополняющие их до 180 0 углы (CK0P) и (CK1P) равны, как вписанные в одну и ту же окружность (K0K1CP) и опирающиеся на одну и ту же дугу (CP).
На основании этого заключаем, что треугольники (K0PM0) и (K1PM1) подобны, и следовательно,
|

Напишем следующую производную пропорцию:
|

Но (D1-D0) есть не что иное, как изменение дистанции между кораблями (DD), а ( ) есть изменение расстояния от уравнителя до полюса (DrК), и, следовательно,
) есть изменение расстояния от уравнителя до полюса (DrК), и, следовательно,
|

Подставив выражения (1.4) и (1.6) в выражение (1.3) и принимая  ,(при Dt ®0) получаем:
,(при Dt ®0) получаем:
|
|

откуда
jк = qр
Однако, ранее было доказано, что
jк = jм
|
jк = jм = qp
Таким образом, теорема доказана полностью.
Теорема 2. При маневрировании двух кораблей относительно друг друга расстояния от них до полюса маневрирования пропорциональны их скоростям хода и изменяются с течением времени пропорционально изменению дистанции между маневрирующими кораблями.
Обозначим начальное и конечное расстояние от маневрирующего до полюса соответственно значками ( ) и (
) и (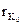 ).
).
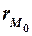 = M0P
= M0P
и
 = M1P
= M1P
Рассмотрим треугольники (K0PK1) и (M0PM1) Их углы
ÐK0PK1 = ÐM0PM1 = q
и
ÐK1K0P = jК = ÐM0PM1 = jМ
Следовательно, треугольники (K0PK1) и (M0PM1) подобны, и мы можем написать, что
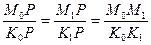
или


Считая, что за малый промежуток времени (Dt) пути кораблей относятся как их скорости хода, получаем окончательно:

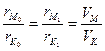
т.е. расстояния от кораблей до полюса маневрирования пропорциональны их скоростям хода.
На основании ранее доказанного (см. теорему 1) подобия треугольников (K0PM0) и (K1PM1) мы можем написать, что


или, применяя введенные обозначения,
|
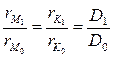
откуда можем написать следующие производные пропорции:
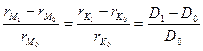
или


Из последнего выражения следует, что с течением времени расстояния от кораблей до полюса маневрирования изменяются пропорционально изменению дистанции между кораблями, и таким образом теорема доказана полностью.
Теорема 3. При маневрировании двух кораблей относительно друг друга расстояние от каждого из кораблей до полюса равно дистанции между кораблями, умноженной на отношение скорости хода данного корабля к относительной скорости.
Построим при точке (М0) путевой треугольник (M1¢M0 M1) и соединим точку (M1¢) с (K0).
Треугольник (M1¢M0 K0) является треугольником позиций (Рис.1) и в нем ÐM1¢M0 K0 = qρ - относительному курсовому углу, а ÐM1¢ K0M0 = q - изменению пеленга за промежуток времени (Dt).
Отсюда заключаем, что
D M0M1¢K0 » D M0M1P» D K0 K1P
Из подобия этих треугольников мы можем написать, что
 и
и 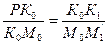
или, применяя ранее введенные обозначения,
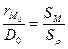 и
и 
Считая, что за малый промежуток времени (Dt) пути кораблей относятся как их скорости и помножив в последних выражениях правые и левые части на (D0), мы получаем окончательно:
|
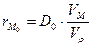 и
и 
что и требовалось доказать.
Теорема 4. При маневрировании кораблей относительно друг друга разность пеленгов с них на полюс равняется разности курсов кораблей.
Рассмотрим треугольники (D M0M1¢ M1), (D M0K0P) и (DM1K1P).
На основании ранее доказанного (см. теорему 3-ю) подобия треугольников (D M0M1¢ K0), (D M0M1P) и (D K0K1P) мы имеем, что:
 |

а также можем написать, что:
Откуда легко написать следующие произвольные пропорции:
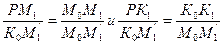
Заменив в этих выражениях (K0K1) равным ему отрезком (M1M1¢) и (K0 M1¢) отрезком (K1 M1), получаем:
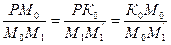
и

на основании чего заключаем, что треугольники (M0K0P), (M1K1P) и (M0M1¢M1) подобны.
Тогда
Ð K0PM0 =Ð K1PM1 = Ð M1¢ M1M0
|
K0PM0 =Ð K1PM1 = x,
что и требовалось доказать.
Теорема 5. При маневрировании кораблей относительно друг друга пеленг с каждого на них на полюс изменяется с течением времени одинаково с изменением взаимного пеленга между маневрирующими кораблями.
Изменение пеленга с маневрирующего на полюс изображено на рис.1 углом (M0PM1) а изменение пеленга с уравнителя углом (K0P K1).
Однако, как было сказано выше (см. теорему 2),
Ð M0PM1 = ÐM0CM1 = q,
так как они вписаны в одну и ту же окружность (M0M1CP) и опираются на одну и ту же дугу (M0M1), а Ð K0PK1 = ÐK0CK1 = q, - как вписанные в одну и ту же окружность (K0K1CP) и опирающиеся на одну и ту же дугу (K0K1).
|
Ð M0PM1 =Ð K0PK1= q,
что и требовалось доказать.
При рассмотрении элементов треугольника позиций (M0M1¢K0) было показано[КВВ2],[2]что, применяя метод относительного движения к изучению вопросов двухстороннего маневрирования, мы получаем возможность переходить от сложного случая маневрирования двух кораблей относительно друг друга - к более простому случаю маневрирования одного из них (маневрирующего) и отношении другого (уравнителя). рассматриваемого в этом случае как неподвижный. При этом, было установлено, что вектор относительного перемещения (M0M1¢) полностью характеризует изменения, происходящие с течением во взаимном расположении кораблей.
На основании изучения свойств полюса маневрирования, сделанного в приведенных выше пяти теоремах, мы приходим к выводу, что об изменении с течением времени во взаимном расположении двух маневрирующих относительно друг друга кораблей можно судить также и на основании того, как происходит изменение положения любого из маневрирующих кораблей относительно полюса маневрирования.
Действительно (рис. 1) треугольник (M0M1P) можно рассматривать как треугольник позиций (M0M1¢ K0), отнесенный к точке (P), увеличенный в  раз и повернутый относительно осей координат (меридиана места или начального пеленга) на угол (aМ), причем
раз и повернутый относительно осей координат (меридиана места или начального пеленга) на угол (aМ), причем
|
Роль вектора относительного перемещения (M0M1¢) играет в этом случае вектор перемещения маневрирующего (M0M1).
Подобным же образом треугольник (K0K1P) можно рассматривать как треугольник позиций (M0M1¢ K0), отнесенный к точке(P), увеличенный в  раз и повернутый относительно осей координат на угол (aК), причем как это видно из рисунка,
раз и повернутый относительно осей координат на угол (aК), причем как это видно из рисунка,
|
Таким образом, при маневрировании двух кораблей относительно друг друга и при известных положениях и аргументах движения относительно полюса одного из них (маневрирующего или уравнителя), изменение взаимного расположения кораблей по пеленгу и расстоянию определяется вектором перемещения (абсолютного) данного корабля относительно полюса маневрирования при условии уменьшения линейного масштаба в  раз, если задано движение маневрирующего, или в
раз, если задано движение маневрирующего, или в 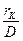 раз - при заданном движении уравнителя, и при условии поворота осей координат соответственно на угол
раз - при заданном движении уравнителя, и при условии поворота осей координат соответственно на угол
(a М= qr - q М) или (aК = qr- qК).
На основании этого можем написать, что
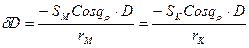

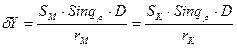

откуда при бесконечно малом (t):
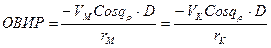

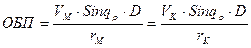
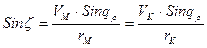
Выражения (1.16) могут быть сформулированы словесно следующим образом: При маневрировании двух кораблей относительно друг друга:
1. Общий ВИР равен величине изменения расстояния от любого из кораблей до полюса, умноженной на дистанцию между кораблями и деленной на расстояние от этого корабля до полюса.
2. Общее БП равно боковому перемещению любого из кораблей относительно полюса, умноженному на дистанцию между кораблями и деленному на расстояние от этого корабля до полюса.
3. ВИП равен величине изменения пеленга с любого из кораблей на полюс.
Date: 2015-07-17; view: 330; Нарушение авторских прав; Помощь в написании работы --> СЮДА... |