Среднее время работы объекта до отказа

На практике чаще пользуются следующим выражением

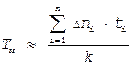(10)

где: t_i - время исправной работы i-ого элемента в партии;

k - количество элементов в партии.

Dn_i - кол-во отказавших объектов в i-ом интервале;

t_срi - среднее значение времени в i-ом интервале.

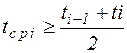
9. Определение показателей надежности при распределении времени возникновения от­казов по экспоненциальному закону.

Экспоненциальное распределение

Пусть известно, что время работы объекта до отказа хорошо согласуется с экспоненциальным распределением, функция и плотность распределения которого соответственно имеют вид

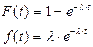(29)

Вероятность безотказной работы для экспоненциального распределения

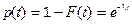(30)

Частость отказов

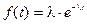(31)

Интенсивность отказов

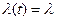(32)

Среднее время работы объекта до отказа

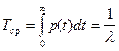(33)

Экспоненциальный закон распределения времени работы объекта до отказа является хорошей аппроксимацией для описания характеристик надежности аппаратуры в период ее нормальной эксплуатации, когда можно пренебречь влиянием старения элементов и считать интенсивность отказов постоянной.

10. Определение показателей надежности при распределении времени возникновения от­казов по нормальному закону.

Нормальное распределение (распределение Гаусса)

Пусть известно, что время работы объекта до отказа хорошо согласуется с распределением Гаусса, функция распределения вероятности и плотность распределения вероятностей которого имеет следующий вид

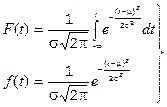, (34)

Определим вероятность безотказной работы для нормального закона

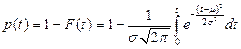
Нормированные функции Лапласа, которые имеют следующий вид

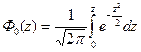(35)

Вероятность безотказной работы, учитывая (35), будет равна

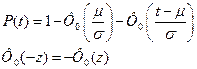(36)

Интенсивность отказов определяется по выражению

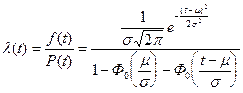(37)

11. Взаимосвязь между основными показателями надежности.

Date: 2015-07-17; view: 671; Нарушение авторских прав