Расчет вероятности безотказной работы сложных систем

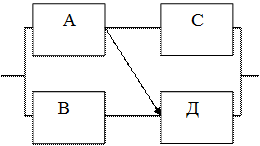
На практике встречаются системы, для описания которых параллельное или последовательное соединение не годится. Рассмотрим в качестве примера систему, изображённую на рис.16.3.

Рис. 16.3. Система со сложным соединением элементов

В данной системе отказ элемента А нарушает сразу два пути - АС и АД. Таким образом, это соединение не является параллельным. Последовательным такое соединение назвать также нельзя: в случае отказа элемента С система остаётся работоспособной.

Для определения вероятности безотказной работы системы или надёжности функционирования системы используют несколько методов. Здесь принят метод прямого перебора. Метод состоит в том, что рассматриваются все возможные способы появления отказов, т.е. не отказал ни один элемент, отказал один элемент, два и т.д.

В системе, изображённой на рис.2, элементы имеют следующие вероятности безотказной работы:

Р(А) = 0,9; Р(В) =0,8; Р(С)= 0,6; Р(Д) = 0,7.

Здесь А - событие «элемент А работает безотказно», тогда Ā – событие «элемент А отказал». Аналогично определяются события для всех остальных элементов. Затем вычисляется вероятность состояния системы для каждого способа появления отказа. Результаты записываются в табл.16.1.

Расчет надежности

Таблица 16.1

№	Число отказавших элементов	Событие, характеризующие состояние системы	Вероятность состояния системы	Отметка о работоспособности системы, изображённой на рис. 3
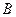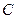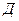
		∩ ∩ ∩	0,3024	+
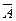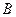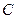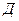
		∩ ∩ ∩	0,0336	+
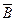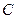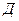
		∩ ∩ ∩	0,0756	+
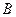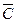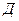
		∩ ∩ ∩	0,1295	+
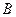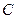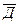
		∩ ∩ ∩	0,2016	+
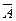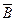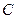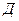
		∩ ∩ ∩	0,0084	-
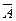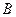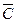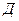
		∩ ∩	0,0144	+
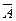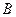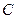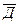
		∩ ∩ ∩	0,0224	-
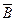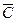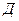
		∩ ∩ ∩	0,0324	+
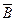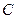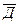
		∩ ∩ ∩	0,0504	+
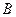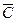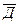
		∩ ∩ ∩	0,0864	-
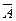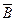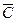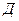
		∩ ∩ ∩	0,0036	-
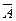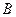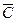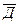
		∩ ∩ ∩	0,0096	-
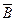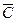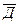
		∩ ∩ ∩	0,0056	-
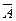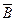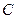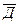
		∩ ∩ ∩	0,0216	-
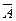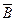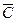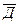
		∩ ∩ ∩	0,0024	-
		∑	1,0000	0,8400

Таким образом, система со сложным соединением элементов (подсистем) имеет вероятность безотказной работы 0,84.

Date: 2015-07-17; view: 1258; Нарушение авторских прав