Умножение матриц

Замечание. Так исторически сложилось, что этим термином «умножением» названа весьма специфическая операция, а не (ожидаемая по аналогии со сложением матриц) операция поэлементного умножения. Тем не менее, есть ряд причин оправдывающих использование слова «умножение». См. ниже.

Определим сначала умножение строки на столбец.

Пусть 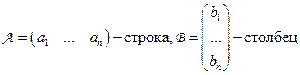, тогда 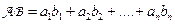- число (или матрица (1x1)).

Перейдём к общему случаю.

Перемножать можно только матрицы согласованного размера и в определённом порядке.

Произведение матриц АВ определено только в случае когда длина строки матрицы А равна длине столбца матрицы В, т.е. А- матрица (kx n), B- матрица (n x l).

Матрицу А будем писать, как набор строк, а матрицу В, как набор столбцов.

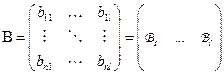
Тогда матрица АВ будет иметь размер (kx l)

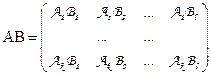
Примеры:

1)

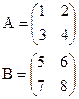(2x2), (2x2).

В этом случае определены оба произведения АВ и ВА.

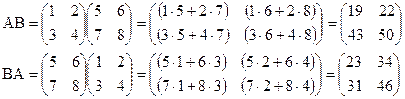
Как видим АВ 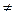ВА – порядок умножения существенен даже для квадратных матриц одинакового размера.

Замечание. Бывает, что для квадратных матриц АВ=ВА, тогда говорят, что матрицы А и В коммутируют.

2)

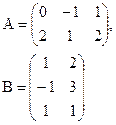
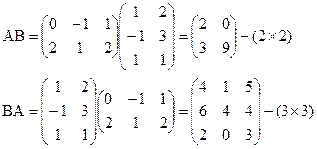
Пример умножения квадратной матрицы на столбец:

3) 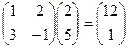здесь умножение в обратном порядке неосуществимо, как и в следующем примере умножения строки на квадратную матрицу:

4)

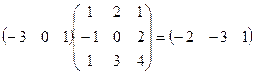
Операция умножения матриц обладает следующими свойствами:

1) (АВ)С=А(ВС) (ассоциативность)

2) (А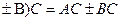

3)

4)

Свойства имеют место для любых матриц А,В,С и чисел 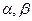, для которых выполняются все записанные операции.

Единичная матрица.

Среди квадратных матриц размера n x n, есть матрица, которая ведёт себя по отношению к операции умножения как единица среди действительных чисел. Т.е. умножение на такую матрицу не меняет умножаемую матрицу.

Такая матрица называется единичной и обозначается буквой I (размер матрицы обычно виден из контекста).

Пример:

1) 2) 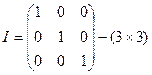и т.д.

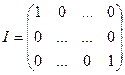
Имеет место следующее утверждение:

Утверждение. Для любых (не обязательно квадратных) матриц А и В, для которых определены АI и IB, будут выполнены равенства: AI=A и IB=B.

Таким образом, единичная матрица ведёт себя как единица, при умножении её на любую матрицу, на которую её можно умножить справа или слева.

Замечание. Среди матриц (n x n) существуют только одна матрица, удовлетворяющая свойствам приведённого утверждения, а именно указанная матрица I.

Действительно, если бы их было две 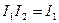и 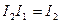, следовательно .

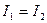Date: 2015-07-17; view: 1020; Нарушение авторских прав