Линейных уравнений

Теорема:

Всякая система линейных уравнений или не имеет решений, или имеет единственное решение, или имеет бесконечное число решений.

Доказательство:

К любой системе линейных уравнений применим метод Гаусса, т.е. расширенная матрица системы приводится к ступенчатому виду. Если ступенька матрицы содержит строку (0 0 … 0 не ноль), т.е. имеющую только один последний ненулевой элемент, то система будет иметь следствием уравнение 0х1 + … + 0хn = не ноль, которое не имеет решений, а значит и вся система не имеет решений.

Если ступенчатая матрица содержит длинную ступеньку (длину > 1) и не выполнен предыдущий рассмотренный случай

1

0 1

0 0 0 0 0

то, очевидно, система будет иметь бесконечное число решений, т.к. не начальным позициям длинной ступени будут соответствовать свободные переменные (одна или несколько), которым можно придать любые значения. И, наконец, если в ступенчатой матрице все ступени, кроме последней, длины 1, а последняя длины 2,

1

Система будет очевидно иметь единственное решение.

Теорема:

Если в системе линейных уравнений число уравнений меньше числа неизвестных, то система не может иметь единственного решения, и возможна только одна из 2-х ситуаций: нет решений или бесконечное число решений.

Доказательство:

В ступенчатой форме расширенной матрицы в случае единственного решения все ступени до черты имеют длину 1, а значит число строк расширенной матрицы (т.е. число уравнений) не меньше числа столбцов до черты (т.е. числа неизвестных).

Замечание:

Если уравнений больше чем неизвестных, то возможны все три указанные выше ситуации. Приведем простые примеры:

x + y = 2 х + y = 2

x + y = 3 - нет решений, x – y = 1 - одно решение,

x + y = 1 2x + 2y = 4

x + y = 2

2x + 2y = 4 - бесконечное число решений.

3x + 3y = 6

Выясним, когда система n уравнений с n неизвестными будет иметь единственное решение.

Теорема:

Система n линейных уравнений с n неизвестными имеет единственное решение тогда и только тогда, когда определитель матрицы системы не равен нулю.

Доказательство:

Рассмотрим систему

а11 х1 + … + а1n xn = b1

…

an1 x1 +… + ann xn = bn

Если = 0, то для решения системы можно применить метод Крамера (или обратной матрицы) и, значит, система имеет единственное решение.

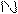а11 … аn1 b1

Её расширенная матрица: А = … …

an1... ann bn

Если система имеет единственное решение, то её расширенная матрица может элементарными преобразованиями быть приведена к такому ступенчатому виду:

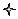1 0 0 … 0 b1

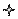
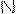0 1 0 … 0 b2

А = …

0 0 … 1 bn

Часть А до черты будет единичной матрицей. Её определитель = 1.

Заметим, что получен из элементарными преобразованиями строк.

Нетрудно проверить, что элементарные преобразования не меняют свойства определителей быть равными или не равными нулю.

Определитель = 1 = 0, а, следовательно, = 0.

Date: 2015-07-17; view: 456; Нарушение авторских прав