Дифференцирование неявной функции

Функция z = ƒ (х; у) называется неявной, если она задается уравнением

неразрешенным относительно z. Найдем частные производные 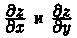неявной функции z, заданной уравнением (44.11). Для этого, подставив в уравнение вместо z функцию ƒ (х; у), получим тождество F(x;у;ƒ (х; у)) = 0. Частные производные по х и по у функции, тождественно равной нулю, также равны нулю:

откуда

Замечания.

а) Уравнение вида (44.11) не всегда определяет одну переменную как неявную функцию двух других. Так, уравнение х²+у²+z²-4=0 определяет функции 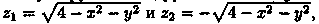определенные в круге х²+у²≤4, определенную в полукруге х2+у2 ≤ 4 при у≥ 0 и т. д., а уравнение cos(x + 2у +3z)- 4 = 0 не определяет никакой функции.

Имеет место теорема существования неявной функции двух переменных: если функция F(x; у; z) и ее производные F'x(x; у; z), F'y(x; у; z), F'z(x;y;z) определены и непрерывны в некоторой окрестности точки M0(x₀;y₀;z₀), причем F(x₀;y₀;z₀)=0, а F'z(x₀;y₀;z₀)≠0, то существует окрестность точки М₀, в которой уравнение (44.11) определяет единственную функцию z=ƒ(х;у), непрерывную и дифференцируемую в окрестности точки (х₀;у₀) и такую, что ƒ(х₀;у₀)=z₀.

б) Неявная функция у=ƒ(х) одной переменной задается уравнением F(x;у)=0. Можно показать, что в случае, если удовлетворены условия существования неявной функции одной переменной (имеется теорема, аналогичная вышеуказанной), то производная неявной функции находится по формуле

Пример 6. Найти частные производные функции z, заданной уравнением e^z+z-х²у+1=0.

Решение: Здесь F(x;y;z)=e^z+z-х²у+1, F'_x=-2ху, F'_y = -х2, F'_z=e^z+1. По формулам (44.12) имеем:

Пример 7. Найти если неявная функция у=ƒ(х) задана уравнением у³+2у=2х.

Решение: Здесь F(x;у) = у³+2у-2х, F'_x=-2, F'_y = 3у²+2. Следовательно,

Методическое обеспечение контроля знаний студентов, обучающихся по направлению 020400 «Биология» при изучении дисциплины

«Математика и математические методы в биологии».

Программа обучения по дисциплине «Математика и математические методы в биологии» для студентов, обучающихся по специальности - 020400 Биология (естественнонаучное образование), квалификация (степень) бакалавр, профиль Генетика - включает в себя теоретическую (лекционный курс и семинарские занятия) и практическую подготовку (практические занятия). Обучение проводится в течение первого, второго, третьего и четвертого семестра и включает в себя 27 лекций (54 часа), 96 часа аудиторной практической подготовки, 66 часов внеаудиторной самостоятельной работы и 36 часов подготовки к экзамену (всего 252 часа).

Текущий контроль знаний осуществляется на каждом занятии в виде устного опроса, тестового контроля, проверки качества выполненной практической работы. Промежуточный контроль проводится по каждому семестру в форме зачета. Итоговый контроль проводится в форме экзамена.

Date: 2016-08-30; view: 471; Нарушение авторских прав