Системы линейных алгебраических уравнений

Системой т линейных уравнений с п неизвестными х _1, х ₂, …, х_п называется система вида

(1.6)

Здесь – вещественные числа, называемые коэффициентами системы, – вещественные числа, называемые свободными членами,

Решением системы (1.6) называется такая упорядоченная совокупность чисел (), которая будучи подставленной в каждое уравнение системы вместо неизвестных превращает их в тождества.

Система (1.6) называется совместной, если она имеет хотя бы одно решение. В противном случае называется несовместной.

Матрица – основная матрица системы;

матрица – расширенная матрица системы.

– матричная форма системы (1,6).

Здесь – матрица-столбец неизвестных,

– матрица-столбец свободных членов.

Система уравнений (1.6) совместна тогда и только тогда, когда ранг основной матрицы системы равен рангу расширенной матрицы, т. е. (теорема Кронекера – Капелли).

Если и , то система (1.6) имеет единственное решение, которое находится

либо матричным способом , (1.7)

либо по формулам Крамера (1,8)

где – определитель матрицы, полученной из основной матрицы заменой i -го столбца столбцом свободных членов.

В общем случае при решении совместной системы (1.6) выделяют базисный минор и базисные неизвестные (неизвестные, коэффициенты при которых образуют базисный минор основной матрицы). Исходную систему заменяют равносильной, состоящей из тех уравнений и k базиcных неизвестных, в которые вошли элементы базисного минора. Полученную систему решают либо матричным способом, либо по формулам Крамера, либо методом Гаусса, выражая базисные неизвестные через остальные свободные неизвестные.

Примеры

16. Три судна доставили в порт 6000 т чугуна, 4000 т железной руды и 3000 т апатитов. Разгрузку можно производить как непосредственно в железнодорожные вагоны для последующей доставки потребителям, так и на портовые склады. В вагоны можно разгрузить 8000 т, а остаток груза придется направить на склады. Необходимо учесть, что поданные в порт вагоны не приспособлены для перевозки апатитов. Стоимость выгрузки 1 т в вагоны составляет соответственно 4,30; 5,25 и 2,20 ден. ед., при отправке на склад – 7,80; 6,40 и 3,25 ден. ед. Записать в математической форме условия полной разгрузки судов, если затраты на нее должны составить 58 850 ден. ед.

Р е ш е н и е. По условию задачи доставленные в порт чугун, железную руду и апатиты можно разгрузить двумя способами: либо в железнодорожные вагоны, либо в портовые склады. Обозначим через количество груза (в тоннах) i -го вида , которое предполагается разгрузить -м способом . Таким образом, задача содержит шесть неизвестных.

Условие полной разгрузки чугуна можно записать в виде:

где – части чугуна, разгружаемого соответственно в вагоны и склады.

Аналогичное условие должно выполняться и для железной руды:

Что же касается апатитов, то их можно разгружать только на склады, а поэтому неизвестная и условие полной разгрузки апатитов принимает вид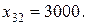

Условие полной загрузки всех поданных в порт вагонов запишется так:

Затраты на разгрузку по условию определены в 58 850 ден. ед., что можно выразить записью:

Итак, с учетом сложившейся в порту ситуации условия полной разгрузки прибывших судов выражаются системой линейных уравнений:

17. Исследовать систему линейных уравнений; если она совместна, то найти ее решение:

Р е ш е н и е. Запишем расширенную матрицу системы и приведем ее к ступенчатому виду с помощью элементарных преобразований:

~ .

Система совместна, т. к. ранг матрицы системы равен рангу расширенной матрицы . Количество неизвестных также равно Значит, система определена, т. е. имеет единственное решение. Запишем систему уравнений, соответствующую полученной расширенной матрице:

Из второго уравнения Подставляя это значение в первое уравнение, получим

Итак, решение системы .

18. Методом Гаусса решить систему уравнений:

Р е ш е н и е. Произведем элементарные преобразования системы:

~ ~

~ ~ .

Так как 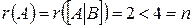, то система совместна и неопределенна (т. е. имеет бесконечное множество решений).

Число базисных неизвестных равно 2, число свободных неизвестных равно 4–2=2. Выберем какой-нибудь не равный нулю минор второго порядка полученной матрицы, например, минор . Его столбцы (первый и второй) соответствуют неизвестным и – это будут базисные неизвестные, а и – свободные неизвестные. Запишем систему уравнений, соответствующую полученной расширенной матрице:

Теперь запишем эту систему в другом виде (слева остаются только базисные неизвестные):

Из второго уравнения выразим через и : . Подставляя выражение для в первое уравнение, получаем . Обозначим свободные неизвестные: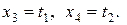

Запишем общее решение системы:

19. Решить систему уравнений, используя формулы Крамара

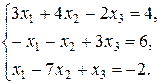
Р е ш е н и е. Вычислим определитель основной матрицы системы:

Система имеет единственное решение. Вычисляем

Отсюда

Таким образом, система имеет единственное решение .

Date: 2016-07-25; view: 637; Нарушение авторских прав