Задачи для самостоятельного решения

Квадратичные формы

Квадратичной формой от п переменных называется сумма (функция) вида ,

где – вещественные числа (коэффициенты), .

Матричная запись квадратичной формы ,

где – матрица квадратичной формы, .

Квадратичная форма называется положительно (отрицательно) определенной, если для всех значений переменных, не равных нулю одновременно.

Для того чтобы квадратичная форма была положительно определенной, необходимо и достаточно, чтобы все главные миноры матрицы А были положительны, т. е.

(критерий Сильвестра).

Для того чтобы квадратичная форма была отрицательно определенной, необходимо и достаточно, чтобы главные миноры матрицы чередовали знак с минуса на плюс, т. е. .

Примеры

17. Выяснить, является ли квадратичная форма положительно или отрицательно определенной:

.

Р е ш е н и е. Запишем матрицу квадратичной формы:

.

Найдем главные миноры:

,

.

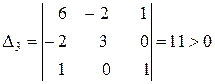Согласно критерию Сильвестра, квадратичная форма положительно определенная.

Задачи для самостоятельного решения

54. Выяснить, являются ли следующие квадратичные формы положительно или отрицательно определенными:

а) ; д) ;

б) ; е) ;

в) ; ж) .

г) ;

ОТВЕТЫ

Глава I

1. .

2. ; 3. ; не существует;

4. ; 6. .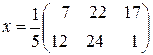

9. ; .

10. а) любое; б) в) .

11. а) –5; б) –5; в) 4.

12. а) abcd; б) abcd; в) г) –16; д) 50.

13. а) ; б) .

14. а) ; б) ;

в) ; г) ;

д) ; е) .

15. а) 3; б) 1; в) 2; г) 3; д) 3; е) 3; ж) 1; з) 2; и) 4.

16. 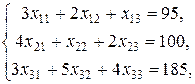где – i -й тип оборудования на -м виде транспорта, .

17. , где i -й вид продукции, .

18.

где – количество груза, отправляемого из станции і в пункт .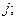

19. а) б) нет решений; в) нет решений;

г) д) ;

е) нет решений; ж) з) нет решений.

20. а) ; б) ; в) ; г) ;

д) ; е) ; ж) .

21. а) ;

б) .

Глава II

2. Точка О – точка пересечения медиан.

3. 1) ; 2) ; 3) .

4. 1) 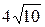; 2) 0.

5.

6. .

7. .

8. 1) – 6; 2) 16; 3) 9; 4) 7.

9. 1) не перпендикулярны; 2) ; 3) ;

4) –1,86; – 4,28; – 5,48; 5) ; ; .

10. 1) ; ; 2) .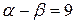

11. .

12. .

13. 1) 6; 2) .

14. .

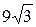15. 1) 24; 2) 60.

16. 1) ; 2) .

17. .

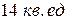18. .

19. 16.

20. .

Глава III

1. а) ; б) ; в) .

2. а) ; б) ; в) .

3. а) ; б) .

4. ,

5. ,

6. а) ; б) ; в) .

7. а) ; б) 5,33; в) ; ;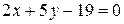

.

8. а) ; б) ; в) .

9. а) ; б) .

10. а) ; б) , прямые параллельны; в) .

11. а) ; б) .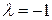

12. , .

13. а) , , б) 4 кв.ед.

14. а) ; б) 3; в) .

15. а) ;

б) 1) ; 2) ; 3) ;

в) 1) ; 2) ; 3) .

16. а) ; б) .

17. .

18. , ,

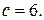
19. а) ; б) .

20. .

21. .

22. а) ; б) .

23. а) 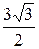; б) 8; в) .

24. а) 1,5; ; б) не параллельны ни при каком ; .

25. а) 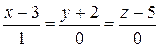; б) ;

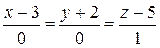в) ; г) ;

д) .

26. .

27. .

28. ; ; .

29. а) б)

30. а) ; б) .

31. а) ; б) ; в) 3 .

32. .

33. а) ; б) .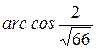

34. а) совпадают; б) скрещивающиеся (перпендикулярны).

35. а) ; б) прямые не параллельны при любом .

36. а) параллельны; б) пересекаются в точке .

37. .

38. .

39. ; прямая не перпендикулярна плоскости при любом m.

40. а) 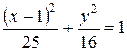– эллипс;

б) – гипербола; в) – парабола.

41. а) – гипербола; б) – эллипс;

в) – эллипс;

г) 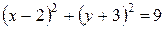– окружность.

42. .

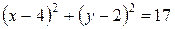43. , , .

44. .

45. .

46. .

47. .

48. .

49. .

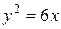50. , .

51. .

52. .

53. .

54. а) положительно определенная; б) не является знакоопределенной;

в) отрицательно определенная; г) положительно определенная; д) положительно определенная; е) положительно определенная; ж) отрицательно определенная.

ЛИТЕРАТУРА

1. Высшая математика: Общий курс: Учебник / А. В. Кузнецов, Л. В. Янчук и др.; Под общей ред. проф. А. И. Яблонского.– Мн.: Вышэйшая школа, 1996.

2. Марков Л. Н., Размыслович Г. П. Высшая математика. Ч. 1. Элементы линейной и векторной алгебры. Основы аналитической геометрии.– Мн.: Амалфея, 1996.

3. Высшая математика: Общий курс: Учебник / Под ред. С. А. Самаля.– Мн.: Вышэйшая школа, 2000.

4. Кузнецов А. В., Кузнецов Д. С. и др. Сборник задач и упражнений по высшей математике. Общий курс: Учебное пособие. – Мн.: Вышэйшая школа, 1994.

5. Гусак А. А. Справочное пособие к решению задач.– Мн.: Вышэйшая школа, 1968.

6. Гусак А. А. Высшая математика.– Мн.: Тетра Системс, 1998.

7. Жевняк Р. М., Карпук А. А. Высшая математика. Аналитическая геометрия и линейная алгебра.– Мн.: Вышэйшая школа, 1992.

ОГЛАВЛЕНИЕ

Глава I. Линейная алгебра

1.1. Матрицы и действия над ними..................................................... 3

1.2. Определитель матриц................................................................... 8

1.3. Обратная матрица........................................................................ 11

1.4. Ранг матрицы................................................................................ 14

1.5. Системы линейных алгебраических уравнений.......................... 17

Глава II. Векторная алгебра

2.1. Векторы на плоскости и в пространстве. Скалярное произведе-

ние векторов........................................................................................ 24

2.2. Векторное и смешанное произведения векторов....................... 30

Глава III. Основы аналитической геометрии

3.1. Уравнения прямой на плоскости................................................. 35

3.2. Взаимное расположение двух прямых на плоскости................. 37

3.3. Уравнения плоскости в пространстве......................................... 39

3.4. Взаимное расположение двух плоскостей.................................. 41

3.5. Уравнения прямой в пространстве............................................. 43

3.6. Взаимное расположение двух прямых в пространстве............. 47

3.7. Прямая и плоскость в пространстве........................................... 49

3.8. Кривые второго порядка............................................................. 51

3.9. Квадратичные формы.................................................................. 58

Ответы................................................................................................ 60

Литература....................................................................................... 66

Учебное издание

ОВСЕЕЦ Михаил Ильич

Date: 2016-07-25; view: 337; Нарушение авторских прав