
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Матрицы и действия над ними
|
|
Овсеец, М. И.
О 34 Сборник задач по высшей математике. Линейная алгебра. Аналитическая геометрия: учеб.-метод. пособие / М. И. Овсеец, Е. М. Светлая.– Минск: Частн. ин-т упр. и предпр., 2006.– 68 с.
Сборник задач содержит краткий теоретический материал, примеры и задачи по разделу «Линейная алгебра. Аналитическая геометрия».
Предназначен для студентов экономических специальностей, изучающих высшую математику Частного института управления и предпринимательства.
УДК 51
ББК 22.11я73
 |
 © Частный институт управления и предпринимательства, 2006
© Частный институт управления и предпринимательства, 2006

Глава I. ЛИНЕЙНАЯ АЛГЕБРА
Матрицы и действия над ними
Матрицей размера 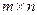 называется прямоугольная таблица чисел, содержащая т строк и п столбцов.
называется прямоугольная таблица чисел, содержащая т строк и п столбцов.
Матрица, у которой число строк равно числу столбцов  , называется квадратной матрицей порядка п. Нулевой называется матрица, все элементы которой равны нулю. Ее обозначают буквой О.
, называется квадратной матрицей порядка п. Нулевой называется матрица, все элементы которой равны нулю. Ее обозначают буквой О.
Диагональной называется квадратная матрица, у которой все элементы, стоящие не на главной диагонали, равны нулю. Диагональная матрица, у которой все элементы главной диагонали равны единице, называется единичной и обозначается буквой Е.
Для матриц одинакового размера вводятся операции сложения и вычитания.
Для того чтобы сложить две матрицы  и
и 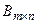 , достаточно сложить их соответствующие элементы. Операция обозначается
, достаточно сложить их соответствующие элементы. Операция обозначается  .
.
Для того чтобы из матрицы  вычесть матрицу
вычесть матрицу 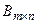 , достаточно из каждого элемента матрицы А вычесть соответствующие элементы матрицы В. Операция обозначается
, достаточно из каждого элемента матрицы А вычесть соответствующие элементы матрицы В. Операция обозначается  .
.
Для того чтобы матрицу  умножить на число
умножить на число  , достаточно все элементы матрицы
, достаточно все элементы матрицы  умножить на число
умножить на число  . Операция обозначается
. Операция обозначается  или
или  .
.
Произведение матрицы  на матрицу
на матрицу  вводится только для согласованных матриц, т. е. число столбцов матрицы
вводится только для согласованных матриц, т. е. число столбцов матрицы  должно равняться числу строк матрицы
должно равняться числу строк матрицы  (число п). Операция обозначается
(число п). Операция обозначается  .
.
Произведением матриц  и
и  называется такая матрица
называется такая матрица  , каждый элемент которой
, каждый элемент которой  равен сумме произведений элементов i -й строки матрицы
равен сумме произведений элементов i -й строки матрицы  на соответствующие элементы j -го столбца матрицы
на соответствующие элементы j -го столбца матрицы  .
.
Произведение матриц не обладает свойством коммутативности, т. е. не всегда  , даже если произведения имеют смысл.
, даже если произведения имеют смысл.
Матрица, полученная из данной заменой каждой ее строки столбцом с тем же номером, называется матрицей, транспонированной к данной. Ее обозначают  .
.
Примеры
1. Найти линейную комбинацию матриц
 где
где  ,
,  .
.
Р е ш е н и е. 
+  .
.
2. Найти произведения  ,
,  матриц:
матриц:
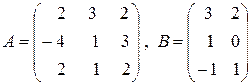 .
.
Р е ш е н и е. Матрица А имеет размерность 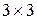 , матрица
, матрица  . Они являются согласованными. Матрица
. Они являются согласованными. Матрица  будет иметь размерность
будет иметь размерность  .
.
 =
=
=  =
= 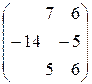 .
.
Произведение  не существует, так как число столбцов матрицы В не равно числу строк матрицы
не существует, так как число столбцов матрицы В не равно числу строк матрицы 
3. Транспонировать матрицу  .
.
Р е ш е н и е. Так как у матрицы А две строки и три столбца, то у матрицы  будет три строки и два столбца:
будет три строки и два столбца:
 .
.
4. Решить матричное уравнение  , если
, если 
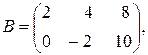 Х – неизвестная матрица.
Х – неизвестная матрица.
Р е ш е н и е. Используя свойства линейных операций над матрицами, найдем Х в общем виде:

Тогда

= 
5. В таблице указано количество единиц продукции, отгружаемой ежедневно на молокозаводах 1 и 2 в магазины М 1, М 2, и М 3, причем доставка единицы продукции с каждого молокозавода в магазин М 1 стоит 50 ден. ед., в магазин М2 – 70, а в М3 – 130 ден. ед. Подсчитать ежедневные транспортные расходы каждого завода.
| Молокозавод | Магазин |
| М1 М2 М3 | |
| 20 35 10 15 27 8 |
Р е ш е н и е. Обозначим через А матрицу, данную нам в условии, а через В – матрицу, характеризующую стоимость доставки единицы продукции в магазины, т. е.
 .
.
Тогда матрица затрат на перевозки будет иметь вид:
 .
.
Итак, первый завод ежедневно тратит на перевозки 4750 ден. ед., второй – 3680 ден. ед.
6. Швейное предприятие производит зимние пальто, демисезонные пальто и плащи. Плановый выпуск за декаду характеризуется матрицей  . Используются ткани четырех типов
. Используются ткани четырех типов  . В таблице приведены нормы расхода ткани (в метрах) на каждое изделие. Матрица
. В таблице приведены нормы расхода ткани (в метрах) на каждое изделие. Матрица  задает стоимость метра ткани каждого типа, а матрица
задает стоимость метра ткани каждого типа, а матрица 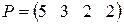 – стоимость перевозки метра ткани каждого вида.
– стоимость перевозки метра ткани каждого вида.
| Изделие | Расход ткани | |||
| Т1 | Т2 | Т3 | Т4 | |
| Зимнее пальто Демисезонное пальто Плащ |
1. Сколько метров ткани каждого типа потребуется для выполнения плана?
2. Найти стоимость ткани, расходуемой на пошив изделия каждого вида.
3. Определить стоимость всей ткани, необходимой для выполнения плана.
4. Подсчитать стоимость всей ткани с учетом ее транспортировки.
Р е ш е н и е. Обозначим через А матрицу, данную нам в условии, т. е.
 .
.
Тогда для нахождения количества метров ткани, необходимой для выполнения плана, нужно матрицу Х умножить на матрицу А:

=  .
.
Стоимость ткани, расходуемой на пошив изделия каждого вида, найдем, перемножив матрицы А и СТ:
 .
.
Стоимость всей ткани, необходимой для выполнения плана, определится по формуле
 .
.
Наконец, с учетом транспортных расходов вся сумма будет равна стоимости ткани, т. е. 9472 ден. ед., плюс величина
 .
.
Итак, 
Date: 2016-07-25; view: 331; Нарушение авторских прав