Пример функции, непрерывной, но не дифференцируемой в данной точке.

Примером такой функции является функция f(x) = |x| (рис.), которая непрерывна, но не дифференцируема в нуле. Напомним, что

Непрерывность функции f (x)=|x| в любой точке (в том числе и в нуле) очевидна.

Рассмотрим график этой функции. Для любого х>0 в некоторой окрестности точки x₀>0 функция равна х, и поэтому производная ее в таких точках равна х', т. е. |x|’=1 при х>0. Так как |х| = —х при х<0, то |x|'= —1 при отрицательных значениях х. В точке 0 функция f(x)=|x| не имеет производной.

Докажем это методом от противного. Допустим, что f(х)=|x| имеет производную в нуле, т. е. Δf(0)/Δx стремится к некоторому числу А при Δx→0. Тогда при всех достаточно малых |Δx| значения Δf/Δx близки к А, и, в частности, при малых значениях Δx должно выполняться неравенство

При Δx>0 справедливо неравенство |1—A|<1, откуда —1<1—A< 1, т. е.

0<A<2. (1)

Для Δx<0 справедливо неравенство |—1—A|<1, откуда —1<—1—A<1, т. е.

—2<A<0. (2)

Неравенства (1) и (2) противоречивы. Следовательно, наше допущение о существовании производной функции f(х)=|x| в нуле неверно. Итак,

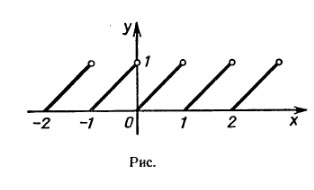Пример функции, не являющейся непрерывной. Практически все функции, с которыми вы встречались до сих пор, непрерывны в любой точке своей области определения. Не следует, однако, считать, что это верно для любой функции. Рассмотрим функцию f (х)={х}, где {х} — дробная часть числа х (график f(x) = {x} изображен на рис.), и возьмем любую целочисленную точку оси абсцисс, например х = 2. Основное свойство непрерывной в х0 функции (f (х0 + Δx)→f(x0) при Δх→0) в данном случае не выполняется. Действительно, пусть Δx→0. Если Δх>0, то {х0 + Δx} близко к нулю. Если же Δx<0, то значения {x0 + Δx} близки к 1. В то же время функция f (х) = {х) непрерывна во всех точках, отличных от точек х=n, где n — целое число. Это свойство функции f (x) = {x) нетрудно понять, рассмотрев рис.

Вопрос 17.