Д. Мощность в цепи с конденсатором.

Если в цепи с конденсатором емкостью С (рис. 2.10) проходит ток i, изменяющийся по синусоидальному закону

,

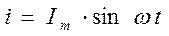то напряжение u, приложенное к этому конденсатору, будет равно

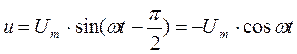
Мгновенная мощность в цепи с конденсатором 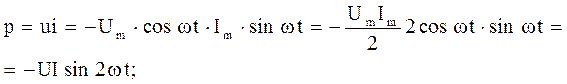(2.24)

Размерность: B_C=wC Ом^-1=См, X_C=1/wC – Ом.

Мощность в цепи с конденсатором, подключенным к источнику с синусоидальным напряжением, изменяется по синусоидальному закону с двойной частотой (рис. 2.11)

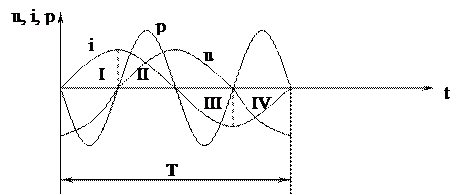Рис. 2.11. Временная диаграмма изменения мощности в цепи с конденсатором.

Активная мощность p в рассматриваемой цепи имеет нулевое значение (p=0).

Изменение мгновенной мощности p по синусоидальному закону происходит с двойной частотой 2ω, причём:

- во II и IV четверти периода, равного T, мощность (энергия) источника накапливается в электрическом поле конденсатора. Максимальное значение энергии, накапливаемой в электрическом поле конденсатора, равно

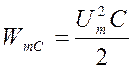
- в I и III четверти периода Т эта мощность из электрического поля конденсатора возвращается к источнику.

Таким образом, в цепи переменного тока с конденсатором происходят колебания мощности между источником и электрическим полем конденсатора.

Величина реактивной мощности в цепи конденсатора определяется выражением

(2.25)

Из временных диаграмм (рис. 2.9, 2.11) видно, что мощность в цепи конденсатора изменяется в противофазе с мощностью в цепи с идеальной катушкой. Поэтому в аналитическом выражении мощности в цепи с конденсатором (2.24) стоит знак «-».

2.4 Неразветвлённая цепь синусоидального тока с активным сопротивлением, индуктивностью и ёмкостью. Треугольники напряжений, сопротивлений и мощностей.

Если в неразветвлённой цепи с R, L и C элементами (рис. 2.12, а) протекает синусоидальный ток 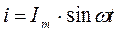, то он создаёт падение напряжений на всех участках цепи:

,

,

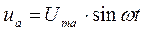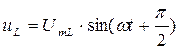Мгновенное значение напряжения цепи определяется по формуле

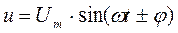
Так как в рассматриваемой цепи включены два реактивных сопротивления X_L и X_C, то возможны три режима работы цепи: 1) X_L>X_C; 2) X_L<X_C; 3) X_L=X_C. Векторная диаграмма напряжений цепи для режима X_L>X_C изображена на рис. 2.12, б).

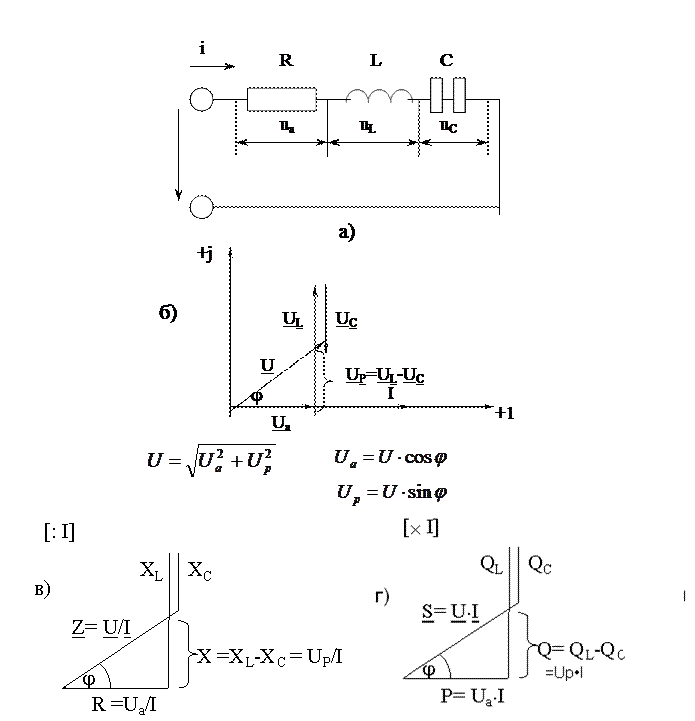
Рис. 2.12. Неразветвлённая R – L – C цепь (последовательный колебательный RLC – контур): а) - электрическая схема, б) – векторная диаграмма напряжений – треугольник напряжений, в) – треугольник сопротивлений, г) – треугольник мощностей.

При построении треугольников напряжений и сопротивлений (рис. 2.12 б, в) приняты следующие обозначения:

U _a= R I и U _P= jX I – активная и реактивная составляющие напряжения;

R и X – активное и реактивное сопротивление цепи;

Z = R+jX (2.26)

– комплексное сопротивление цепи (рис2.12а);

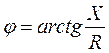
(2.27)

(2.28)

- соответственно полное сопротивление и аргумент комплексного сопротивления Z;

(2.29)

- комплексная мощность или комплекс полной мощности пассивного двухполюсника;

(2.30)

- модуль или полная мощность пассивного двухполюсника;

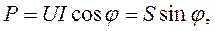(2.31)

(2.32)

- активная и реактивная мощность пассивного двухполюсника.

Из подобия треугольников сопротивлений (рис. 2.12в) и мощностей (рис. 2.12г) следует, что

(2.32а)

Date: 2016-07-25; view: 748; Нарушение авторских прав