Различные способы представления синусоидальных величин.

1. Представление синусоидальных величин вращающимися векторами (рис.2.3).

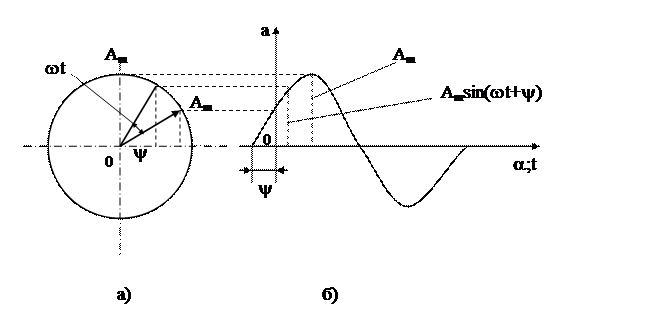
Рис. 2.3 Векторное изображение синусоидальных величин: а) – вращающийся вектор; б) – кривая изменения его проекции на ось Оа.

Применение вращающихся векторов позволяет компактно представить на одном рисунке совокупность различных синусоидально изменяющихся величин одинаковой частоты.

Любую синусоидально изменяющуюся во времени величину можно изображать вращающимся вектором, длина которого равна амплитуде, а угловая скорость вращения – угловой частоте этой синусоидальной величины. Начальное положение вращающегося вектора определяется углом, равным начальной фазе синусоидальной величины y и отклоняемым от положительного направления оси ОХ в сторону, противоположную вращению часовой стрелки.

2. Представление синусоидальных величин с помощью комплексных чисел. Символический метод.

Символический метод или метод комплексных чисел соединяет в себе достоинства аналитического способа с наглядностью, присущей геометрической интерпретации.

Пользуясь понятием «комплексное число» и условным представлением напряжения или тока в виде вектора можно поместить вектор в комплексной плоскости (+j; +1), и выразить его в комплексной форме. Тогда вещественная (действительная) часть будет проекцией вектора на одно направление, а мнимая – на другое, перпендикулярное. (рис. 2.4)

Представление векторов в виде комплексных чисел позволяет заменить геометрические операции над векторами алгебраическими действиями над их комплексами и, таким образом, выполнить любую задачу аналитическим способом.

Рис. 2.4 Представление вектора в комплексной плоскости: · - комплексное число, A _m – комплексная амплитуда, А – комплексное действующее значение синусоидальной величины A = A _m/√2=Ae^iΨ (A<Ψ).

Комплексное число А в общем случае состоит из вещественной А¢ и мнимой А² частей:

А=А¢+jА²

Проекция на вещественную ось +1 соответствует вещественной части комплексного числа -А¢.

Проекция вектора на мнимую ось j (ось ординат) соответствует коэффициенту при мнимой единице j-А².

Мнимая единица j представляет собой поворотный множитель, умножение на который означает поворот вектора на 90^о против часовой стрелки, т.е. поворот в положительном направлении.

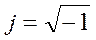
Модуль комплексного числа соответствует длине вектора, изображающего это комплексное число.

Аргумент комплексного числа определяется выражением

и показывает угол, на который повёрнут вектор по отношению к положительному направлению вещественной оси +1.

Таким образом, любой вектор однозначно изображается комплексным числом, соответствующим концу этого вектора, т.е. точке.

Комплексный метод расчёта применим только к цепям с синусоидальными ЭДС, напряжениями и токами, т.к. только синусоидальные величины можно изобразить векторами.

Существуют 3 формы записи комплексного числа:

1) алгебраическая: A =A’+jA” или зачастую записывают так:

где и

- действительная и мнимая составляющие комплексного значения синусоидальной величины:

2) тригонометрическая:

3) показательная:

Переход от показательной формы к тригонометрической выполняется при помощи формулы Эйлера:

(2.1)

Переход от алгебраической формы к показательной и от показательной к тригонометрической выполняется с помощью модуля |A| и аргумента комплексного числа y в соответствии с алгоритмами -(рис.2.5 а, б).

а)

(формула Эйлера)

б)

Рис. 2.5 Алгоритм перехода (представления) синусоидально изменяющегося вектора из одной формы в другую:

а – алгебраической в показательную; б – показательной в тригонометрическую.

Комплекс может быть выражен также в показательной форме:

(2.1¢)

Здесь представляет собой так называемый поворотный множитель, показывающий, вектор длиной А повёрнут относительно положительного направления вещественной оси +1 на угол y.

Если вектор, выраженный комплексом , умножить на комплекс 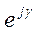, то получим вектор той же длины, но образующий с положительным направлением вещественной оси угол y+g, т.е. вектор, опережающий на угол g:

Для перевода из алгебраической формы в показательную определяют модуль и аргумент по формуле

Сложение и вычитание комплексных чисел производится только в алгебраической форме.

Умножение и деление комплексных чисел можно производить в алгебраической форме, однако это удобнее произвести в показательной форме.

Комплексное число, изображающее производную синусоидальной функции, равно комплексному числу, изображающему саму синусоидальную функцию , умноженному на jw.

Комплексное число, изображающее интеграл синусоидальной функции, равно комплексному числу, изображающему саму синусоидальную функцию , делённому на jw.

Согласно формулы Эйлера (2.1) и (2.1¢) для единичного вектора (А=1) модуль комплексного числа

Умножая правую и левую часть формулы Эйлера (2.1) на I_m, получим

(2.1²)

В общем случае угол y может быть представлен так:

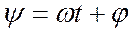(2.2)

Подставляя выражение (2.2) в выражение (2.1²), мы можем представить его в следующем виде:

(2.3)

Теперь представим, что имеет место ток, изменяющий свою форму во времени по синусоидальному закону:

(2.4)

Эта синусоидально изменяющаяся величина (2.4) соответствует мнимой части уравнения (2.3), т.е.:

(2.5)

Обычно комплексное число соответствует определённой синусоиде и запись выполняют для t=0; тогда выражение 2.5 для синусоидального тока можно представить комплексным числом

Левые части этих выражений – это комплексные числа, соответствующие комплексной амплитуде тока I_m и комплексу действующего значения тока I.

Правые части – амплитудное (I_m) и действующее (I) значения тока, повёрнутые на угол j в положительном направлении относительно вещественной оси +1 (см. рис.2.4.)

При этом согласно формуле (2.1):

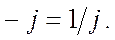(2.6)

Таким образом, поворот вектора А_m на угол ±p/2, соответствует умножению его на ±j; поворот на ±p - умножению его на -1 и т.д.

Пример1:

Пусть имеется синусоидально изменяющееся напряжение, аналитическая запись которого может быть произведена следующим образом

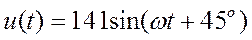
и графически представлена в виде синусоиды, сдвинутой относительно начала системы координат на угол 45^о – рис. 2.6а.

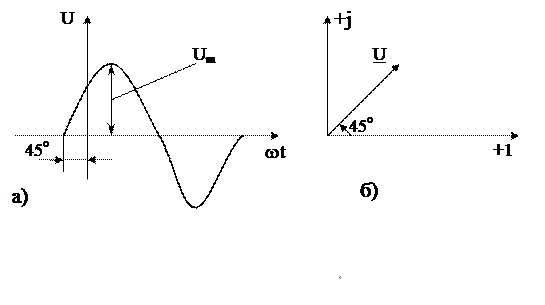
Рис. 2.6 Пример представления комплексного числа двумя способами:

а) – в виде синусоиды sinwt, б) – в виде вектора, расположенного в комплексной системе координат (+j,+1).

Запись действующего значения данного напряжения можно выполнить так:

- см. рис. 2.6 б.

Используя теорему Эйлера (2.1), запись можно произвести и так:

.

Пример 2:

Имеется синусоидально изменяющийся ток

Интерпретация действующего значения данного тока с помощью комплексного числа будет такова: