Интерполяция по методу ЦДА

Интерполяция - получение координат промежуточных точек траекторий движения настроечной точки движения на плоскости или в пространстве.

Известно несколько методов интерполяции, среди которых наибольшее распространение получили:

- метод оценочной функции

- метод цифровых дифференциальных анализаторов (ЦДА),

- метод кодовой интерполяции и

При интерполяции по методу ЦДА моделируется дифференциальное уравнение воспроизводимой кривой. Основным устройством ЦДА является цифровой интегратор, который явл. программным модулем, выполняет приближенное вычисление определенного интеграла по одной из формул численного интегрирования.

Наиболее простое приближенное вычисление определенного интеграла выполняется по первой формуле Эйлера (метод прямоугольника). Погрешность вычислений с интегрированием по методу прямоугольников является удовлетворительной при реализации линейной и круговой интерполяции.

Сущность метода прямоугольников заключается в том, что интегрируемая функция у = f(х) в пределах интегрирования от х₀ до х_m разбивается на m достаточно малых интервалов. Затем каждый из интервалов заменяется площадью построенного на нем прямоугольника. Приближенное значение интеграла определяется суммой этих площадей, расположенных на отрезке интегрирования.

x=m mm

ydx = y_i (х_i+1 -x_i) = y_i x_i

x=0 i=1 i+1

где y_i – значение интегрируемой функции у = f(х)

x_i– приращение независимой переменой

m - число разбиений функций

Если все отрезки функции принять одинаковыми и равными единице, приближенное значение интеграла вычисляется в результате суммирования текущих значений интегрируемой функции yi.

x=m m

ydx = y_i

x=0 i=1

Каждое последующее значение интегрируемой функции y_i+1 может быть получено путем прибавления к предыдущему значению y_i. В общем виде можно записать

m

y_m= y₀ + 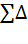y_i

_i=1

При реализации по методу ЦДА линейной и круговой кодовой интерполяции независимой переменной является время τ=1/f, где f — частота вычислений, определяемая частотой следящего привода. Например, для реализации линейной кодовой интерполяции в режиме подготовки данных рассчитываются приращения Δx_τ и Δy_τ по осям координат за время τ

Date: 2016-07-22; view: 1037; Нарушение авторских прав