Механикалық тербелістер. Математикалық маятник.

Механикалық тербелістер – бұл қайталанбалы қозғалыс, бұл кезде дене кеңістіктегі бір орынды қайта-қайта өтеді. Тербелістердің периодты және периодсыз түрлерін ажыратады. Периодты тербелістер – дененің координаталары және басқа сипаттамалары уақыттың периодты функцияларымен сипатталатын тербелістер. Шығу тегіне байланысты тербелістерді еркін,еріксіз, автотербелістер деп бөлінеді. Ал кинематикалық қасиеттерінің уақыт бойынша өзгеруіне байланысты гормоникалық, өшетін және аратәріздес(пилоабразный) болып жіктеледі.

Тербелістердің жалпы сипаттамалары: Тербеліс амплитудасы – дененің тепе-теңдік күйінен ең үлкен ауытқуы(өлшемнің орташа өлшемнен ауытқуы); тербеліс периоды – дененің қозғалысы толық бір рет қайталанатын уақыт(тербелістің барлық кинематикалық сипаттамалары қайталанады), яғни толық бір тербеліс жасайды Т= [секунд]; тербеліс жиілігі – 1 секундта қанша тербеліс жасалатынын көрсететін шама v = [Герц]; Тербеліс жиілігі циклдық жиілікпен және периодпен келесі түрде байланысқан: ω=2πυ=

Математикалық маятник - салмақсыз созылмайтын жіппен оған ілінген материалық нүктеден тұратын механикалық жүйе. Ұзын жіңішке жіпке ілінген шағын ауыр шарик едәуір дәрежеде матем-қ маятниккке жақындайды. L ұзындықты g еркін түсу үдеуіне ие біртекті ауырлық күшінің өрісіндегі математикалық маятник периоды

тең және маятник массасы мен амплитудасына тәуелсіз, бірақ маятниктің ұзындығы мен ауырлық үдеуіне байланысты. Маятниктің тепе-теңдік қалыптан ауытқуы жіптің вертикальмен жасаған бұрышы арқылы сипаттаймыз. Маятник тепе-теңдік қалыптан ауытқыған кезде шама жағынан mgl sin φ-ге тең (m – маятниктің массасы, ал l – оның ұз-ғы) айналдырушы мезет пайда болады. Ол маятникті тепе-теңдік қалпына келтіруге тырысатындай болып бағытталады және бұл жағынан квазисерпімді күшке ұқсас. Айналмалы моментке арналған өрнек мына түрде жазылады:

M= - mgl sin φ.

21.Серіппелі маятник.Физикалық маятник.

Серіппелі маятник – бір басы қатты бекітілген, ал екінші басында m массалы жүк ілінген k қатаңдық коэффициентіне ие серіппеден тұратын механикалық жүйе. Басқаша айтқанда көлемді денеге оны тепе-теңдік жағдайына қайтаратын күш әсер еткенде ол осы қалып төңірегінде тербелістер жасайды. Осыны серіппелі маятник деп атайды. Қарапайым жағдайда серіппелі маятник серіппемен қабырғаға ілінген, горизонталь жазықтық бойынша қозғалатын қатты дене.

Серіппеге ілінген жүкке вертикаль жағдайда ауырлық күші мен серіппенің қатаңдық күші әсер етеді. Алдымен ауырлық күшінің әсерінен ол х₁ ге созылады, артынша осы жағдайдан х ке ауытқиды. Сонда Ньютонның екінші заңына сәйкес: ma=k|x₁+x|-mg бірақ |x₁|= , сонда ma=k| +x|-mg=k|x|. Немесе ma=-kx серіппеде тербелетін дененің үдеуі оған әсер ететін ауырлық күшіне тәуелді емес. Ол тек оны тепе-теңдік күйінен шығарады. Үдеуді көрсетсек: a=- x, алынған үдеуді тербелмелі қозғалыс үдеуімен салыстырсақ a=x``=-ωx². Серіппелі маятниктің тербеліс кезіндегі циклдық жиілігі: ω= . Сонда тербеліс периоды: Т=2π

Физикалық маятник- ауырлық центірінен өтпейтін(масса центірінен), қозғалмайтын горизонталь оське бекітілген және сол оське қатысты еркін тербеле алатын қатты дене. Орнықты тепе-теңдік күйінде физикалық маятниктің О іліну нүктесі және С массалар центрі арқылы өтетін түзу вертикаль бағытталады. Массасы m маятникті тепе-теңдік қалпынан α бұрышқа ауытқытып жіберсек, онда ол массалар центіріне түсірілген ауырлық күшінің құраушысының әсерінен тербелмелі қозғалыс жасайды: F=-mgsinα. Теңдеудегі минус таңбасы ауырлық күшінің құраушысының α бұрышының өсу жағына қарама-қарсы бағытын көрсетеді. Ауырлық күшінің құраушысының О айналу осіне қатысты моменті М=-mgasinα. Мұндағы a О іліну нүктесінен С массалар центіріне дейінгі қашықтық. Физикалық маятниктің қозғалыс теңдеуінің айналу осіне проекциясын мына түрде жазуға болады: I =-mgasinα. Мұндағы I – маятниктің айналу осіне қатысты инерция моменті. Физикалық маятниктің тербеліс периоды T==2π Егер 1 секундтағы тербеліс санын υ деп белгілесек, υ=, ал ω₀==2πυ.

22. Толқындар. Толқынның түрлері. Толқындардың негізгі сипаттамалары. Допплер эффектісі

Егер қатты, сұйық немесе газ тәрізді жүйенің бір жерінде бөлшектің тербелісі қоздырылса, онда ортаның атомдары мен молекулаларының өзара әсерінен тербелістер жүйенің бір нүктесінен келесісіне беріледі. Ортада тербелістің таралу құбылысы толқын деп аталады. Толқындар бойлық және көлденең болады. Егер толқын әсеріндегі жүйе бөлшектері толқынның таралу бағытына перпендикуляр бағытта орын ауыстырса ол көлденің толқын, олар тек қатты ортада болады. Егер толқын әсеріндегі жүйе бөлшектері толқынның таралуына орын ауыстырса ол бойлық толқын, ол барлық материалдық жүйелерде таралады. Сұйықтық бетіндегі толқындар көлденің бағытқа да, бойлық бағытқа да ие болады. Көлденең де, бойлық та толқында толқынның таралу бағытында заттың орын ауысуы болмайды, тек тепе-теңдік күйіне шамалас жағдайда тербелістер жасайды. Бірақ толқындар тербеліс әсерінен бір нүктеден екінші нүктеге энергия тасымалдайды. Механикалық нүктенің ерекшелігі олар материалдық ортада таралады(қатты, сұйық, газды орталар), себебі кинетикалық және потенциалдық энергияларды тіркеу керек. Орта инертті және серіппелі қасиеттерге ие болуы керек. Шынай орталарда бұл қасиеттер бүкіл көлем б/ша таралған. Практикада гармоникалық және синусоидтық толқындар жиі қолданылады. Олар бөлшектің А тербеліс амплитудасымен, υ жиілікпен және λ толқын ұзындығымен сипатталады. Синусоидтық толқындар біртекті ортада тұрақты v жылдамдықпен сипатталады. Синусоидтық толқында орта бөлшегінің y(x,t)тепе-теңдік жағдайынан ауытқуы толқын жайылатын ОХ осіндегі х координаталарына және t уақытқа келесі заңдылық бойынша бағынады: y(x,t)=Acosω(t-)= Acos(ωt-kx). Бұндағы k= - толқындық сан, ω=2πυ – циклдыжиілік. Толқын ұзындығы λ – бірдей фазада тербеліп тұрған ОХ осіндегі екі көрші нүктенің арақашықтығы. λ Ұзындыққа ие толқынды толқын Т периодта өтеді, сондықтан λ = vT, v – толқынның таралу жылдамдығы. Қума синусоидтық толқын уақыт бойынша және кеңістікте периодты. Уақыт бойынша периоды орта бөлшегінің Т тербеліс периодына, кеңістік б/ша периоды λ толқын ұзындығына тең. k=толқындық саны ω= циклдық жиеліктің кеңістіктік аналогы. Қума толқындар кеңістікте толқынның түріне, ортаның инерттілігі мен серпімділігіне тәуелді белгілі бір жылдамдықпен таралады. Көлденең толқындардың тартылған ішектегі н/е резинка қылдағы жылдамдығы μ массаға және Т тартылу күшіне байланысты: v= . Бойлық толқындардың шексіз ортада таралуы орта тығыздығына және Δ p қысымның өзгеруі мен көлемнің Δ V / V қатыстық өзгеруінің пропорционалдық коэффициентінің кері таңбамен алынған мәніне тең В барлық жақтан сығылу моудліне тәуелді: Δ p=-В 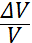. Ал жылдамдығы: v=

Серпімді ортада, толқын көзінен белгілі бір қашықтықта, қабылдағыш деп аталатын, ортаның тербелісін қабылдайтын құрылғы орналасқан делік. Толқын көзі мен қабылдағыш толқын тарайтын ортамен салыстырғанда қозғалмайтын болса, онда қабылдағыш қабылдайтын тербеліс жиелігі толқын көзінің ʋ₀ тербеліс жиелігіне тең. Егер қабылдағыш толқын көзі не олардың екеуі де ортамен салыстырғанда қозғалатын болса, онда қабылдағыш қабылдайтын ʋжиілік ʋ₀ жиіліктен өзгеше болуы да мүмкін. Бұл құбылыс Доплер эффектісі деп аталады. Қарапайым болу үшін, қабылдағыш пен толқын көзі олардың арасын қосатын түзу бойымен қозғалады деп ұйғарайық. Егер толқын көзі қабылдағышқа қарай қозғалса, онда толқын көзінің ʋ_көз жылдамдығы оң деп, ал егер толқын көзі қабылдағыштан алыстаса теріс деп есептейміз. Осы сияқты, егер қабылдағыш толқын көзіне жақындаса, онда ʋ_қаб кабылдағыш жылдамдығын оң деп, ал егер қабылдағыш толқын көзінен қашықтаса теріс деп санаймыз.

Егер толқын көзі қозғалмайтын болса және ʋ₀ жиілікпен тербелсе, онда толқын көзі ʋ₀ –нші тербеліс жасап өткен мезетке бірнеше тербелістен туған толқын “жалы” ортада ʋ жол жүріп үлгереді(ʋ - толқынның ортамен салыстырғандағы таралу жылдамдығы) Олай болса, ʋ₀ секунд ішінде толқын көзі туғызған тоқынның «жалы» мен «сайы» ʋ ұзындықтың ішінде орналасады. Егер толқын ортамен салыстырғанда ʋ_көз жылдамдықпен қозғалса, онда толқын ʋ₀-інші тербеліс жасаған мезетте, бірінші толқыннан туған «жал» толқын көзінен ʋ- ʋ_көз қашықтықта болады. Олай болса, толқынның ʋ₀ “жалы” мен ”ойысы” ʋ- ʋ_көз ұзындығының ішінде орналасады да, толқын ұзындығы мынаған тең болады: (1)

Қозғалмайтын қабылдағыш секунд ішінде, ʋұзындығының ішінде орналасатын “жалдар” мен ”сайлар” өтеді. Егер қабылдағыш ʋ_қаб жылдамдықпен қозғалса, Онда ол секундтық аралық уақыт соңында, осы аралықтың басында қазіргі қалпына ʋ қашықтықта тұрған “сайды” қабылдайды. Сонымен қабылдағыш секунд ішінде ʋ+ ʋ_қаб ұзындығының ішінде орналасқан “жалдар” мен ”сайларға” сай келетін тербелістерді қабылдайды және (2) жиілікпен тербеледі.

(2) өрнегіне ʎ шамасына арналған(1) өрнегін қойып мынаны аламыз: ₀ (3). (3) формуласы бойынша қабылдағыш пен толқын көзінің осындай, олардың ара қашықтығы қысқаратындай, қозғалысында қабылдағыш қабылдайтын ʋ жиілік толқын көзінің ʋ₀ жиілігінен көп үлкен болады. Егер толқын көзі мен қабылдағыштың ара қашықтығы артса, ʋ шамасы ʋ₀ шамасынан кем болады. Толқын көзі мен қабылдағыштың қозғалысы олардың арасын қосатын түзуге дәл келмесе, (3) формуласындағы ʋ_көз мен ʋ_қаб шамаларын толқын көзі мен қабылдағыш жылдамдықтарының аталған түзудегі проекциялары деп түсіну керек.

23. МКТ-негізгі теңдеуі. Температура. Молекулалардың жылулық қозғалысы

Массасы m газдың алғашқы күйін сипаттайтын параметрлердің мəндері P₀, V ₀, Τ₀ болсын. Егер газдың күйі өзгерсе,онда оның соңғы күйін сипаттайтын параметрлер Ρ₁, V ₁, Τ₁болады. Бойль-Мариотт жəне Гей-Люссак заңдары негізінде осы газдың екі күйінің арасындағы байланысты анықтауға болады.Ол

үшін газдың бірінші күйдегі қысымын тұрақты деп (P ₀= const), оны Τ₀-ден Τ₁–ге дейін қыздырамыз. Сонда оның көлемі V₀ -ден V ′ке дейін өзгереді. Бұл процесс изобаралық болғандықтан, Гей-Люссак заңы бойынша көлемнің өзгеруі: V ′ = V ₀(T ₁/ T _0.) Енді газ күйінің соңғы өзгерісін тұрақты температурада (Т= const), оның көлемін өзгертіп байқауға болады: яғни газ қысымыΡ₀-дан Ρ₁-ге дейін өзгерсе, көлемі V ′-ден V ₁-ге ұлғаяды. Бұл өзгеріс изотермиялық болғандықтан,Бойль-Мариотт заңы негізінде V ′ = P₁ (V ₁/ P₀.)Бұл екі қатынастың сол жақтары өзара тең болғандықтан: V ₀ (Τ₁/ Τ₂)= V ₁ (Ρ₁/ Ρ₂).Осы теңдіктің екі жағын да 0 Ρкөбейтіп, 1 Τбөлсек(Ρ₀ V ₀)/ Τ₀=(Ρ₁ V ₁)/ Τ₁.

Сонымен,берілген газ массасы үшін, газ күйінің өзгерісін көрсететін шама (Ρν)/Т əр уақытта тұрақты болады екен, яғни(Ρ V)/Т= const. (7)

Бұл теңдікті бірінші рет француз физигі жəне инженері С.Клапейрон (1799-1864)Бойль-Мариотт жəне Гей-Люссак заңдарын біріктіріп, қорытып шығарғандықтан,ол идеал газ күйін сипаттайтын Клапейрон теңдеуі деп аталады.Қалыпты жағдайда, яғни температура (0 ⁰ С) жəне атмосфералық қысым (Ρ₀ =1,01*10 ⁵ Па) болса, онда кез келген газдың бір молінің көлем22,41 л = 22,41*10⁻³ м3 болады. Сондықтан газдың сандық мəні бір мольге тең болса,(7) теңдіктерге тұрақты шама барлық газдар үшін бірдей болады.Барлық газ үшін тұрақты шаманы R əріпімен белгілеп, оны универсал газ тұрақтысы деп атайды. Сонда (7) теңдік мына түрде жазылады:Ρμ V = RТ. (8). Енді (8)теңдеуден универсал газ тұрақтысының сандық мəнін анықтап шығарайық.Егер Т=273К, Ρ =1,01*10⁵ Па, V = 22,41*10⁻³ м 3 / моль μ, Онда R= =8,31 Дж/(моль·К).

1 мольге ғана дұрыс болатын 0 Ρ V =RT (0 V = V) формуланы кез келген

мөлшердегі массаға қолданатындай өзгертіп жазуға болады. Ол үшін газдың молярлық массасын μ əріпімен белгілейміз. Олай болса, тұрақты қысым мен температурада

(Ρ₁Τ=const), V = (V ₀ m)/μ; P V₀ m/ μ; P V₀ m/ μ= m/ μ RT

P V= (9)

Бұл теңдік массасы m кез келген газ үшін қорытылып шығарылған Клапейрон-Менделеев теңдеуі болып табылады.Универсал газ тұрақтысының физикалық мəнін түсіндірейік. Жеңіл қозғалатын поршені бар цилиндрлі ыдыста көлемі 1 моль газ болсын. Газ жылжымалы поршеньге сыртқы қысымға тең P=const қысым түсіреді. Цилиндр ішіндегі газды 1К температураға қыздырса, оның көлемі ұлғайып, поршеньді h биіктікке көтереді. Поршеньге түсіретін қысым Ρ = F / S Мұндағы F-поршеньге түсірілетін қысым күші, S- поршеньнің ауданы. Сонда қысым күші: F = Ρ S. Газдың поршеньді h биіктікке көтергенде істейтін сыртқы жұмысы A = Fh = Ρ Sh,мұндағы Sh көбейтіндісі газ көлемінің өсімшесін көрсетеді, яғни Δ V = Sh,сонда газ көлемінің ұлғаю кезіндегі жұмыс A = ΡΔ V (10)

Егер газдың алғашқы күйін сипаттайтын теңдеу Ρ V = RT (11)

болса, 1К қыздырғаннан кейінгі көлемі 1 ν=ге өзгеріп, (11) теңдеу басқа түрде көрсетіледі, яғни Ρ V ₁= R (T + 1) (12)

Соңғы (11) жəне (12) теңдеулерден мына теңдік шығады Ρ(V₁ − V) = R. ρΔ V = R (13). Егер де (10) жəне (13) теңдеулерді салыстырсақ, онда универсал газ тұрақтысы істелген жұмысқа тең болады:

A=R (14)Сонымен, универсал газ тұрақтысы 1 моль газды 1К температураға қыздыру үшін кеткен изобаралық жұмысқа тең екен.Температура ұғымының анықтамасына төмендегідей пікірлер арқылы келуге болады. Егер бір-біріне жанасқан бірнеше дене жылулық тепе-тең күйде тұрған болса, яғни жылу беру арқылы энергиямен алмаспаса, онда мұндай денелердің температурасы бірдей болады деп есептейміз. Денелер арсындағы жылу контрактісін орнатқан кезде, олардың біреуі жылу берілу арқылы, екіншісіне энергиясын берсе, онда бірнеше дененің температурасы екіншісінен жоғары болып есептеледі. Денелердің көлемі, электр кедергісі және т.с.с. бірқатар қасиеттері температураға тәуелді болады. Осы қасиеттердің кез келгенін темпратураның сандық анықтамасын жасауға пайдалануға болады.

Температураны өлшеуге арналған денені(термометрлік денені) ери бастаған мұзбен жылулық тепе-теңдікке келтіріп, осы жағдайдағы оның температурасын өлшеу үшін пайдаланғымыз келіп отырған дене қасиетін (темп-ралық белгісін) санмен сипаттайық. Дененің осындай белгісі ретінді оның көлемі тандап алынсын делік. Оның 0°-тағы мәні V₀ болсын. Бұдан кейін осы денені атмосфералық қысымда қайнап жатқан сумен жылулық тепе-теңдікке келтіріп, оның осы күйдегі темрературасын 100° - қа теңестіріп, осыған сәйкес оның V₁₀₀ көлемін анықтайық. Біздің таңдап алған температуралық белгіміз температурамен сызықты түрде өзгереді де термометриялық дененің көлемі V болатын осы күйдің темп-сын

t°= (1)

деп жазуға болады.

Осылайша анықталған температуралық Цельсий шкаласы деп аталатын белгілі. (1)-ге ұқсас қатысты, темп-ны өлшеуге көлем емес, қандай да бір басқа температуралық белгі алынатын жағдай үшін жазуға болады.

Термометрді осы айтылған тәсілмен градуирлеп, оны температураны өлшеуге пайдалануға болады, ол үшін термометрді температурасын өлшегіміз келіп отырған денемен жылулық тепе-теңдікке келтіріп, көлемнің өзгерісіне есептеу жүргіземіз.

Табиғаты түрліше термометриялық денелерді немесе әртүрлі температуралық белгілерді пайдаланатын термометрлерді салыстырған кезде, осы термометрлердің көрсетулері, 0° және 100° болғанда градуирленгендіктен, осы темп-ларда бірдей болып, ал басқа темпера-лардағы көрсетулері бірдей болмайтындығы байқалды. Осыдан, темп-ра шкаласын бір мәнді анықтау үшін, градуирлеу тәсілімен қатар, термометриялық дене мен темп-лық белгіні де таңдап алу жайында келісіп алу қажет.

24. Термодинамикалық жүйе. Термодинамикалық параметрлер. Термодинамикалық процесс. Қайтымды және қайтымсыз процестер.

Термодинамикалық жүйе деп басқа денелермен өзара энергия және зат алмаса алатын бір немесе бірнеше денелер жиынтығын айтады.Газ күйін сипаттайтын макроскопиялық шамаларды газдың термодинамикалық параметрлері деп атайды.Газдың ең маңызды термодинамикалық параметрлері оның V көлемі, p қысымы, Т температурасы болып табылады.Егер газдың белгілі бір m массасын алатын болсақ, онда тұрақты p, V және T кезінде газ тепе-теңдік күйде болады. Осы параметрлер өзгерген кезде газда қандай да бір процесс өтіп жатады. Егер осы процесс бірінің артынан бірі ілескен газдың тепе-теңдік күйлерінің қатарынан тұратын болса, онда бұл процесс тепе-теңдік процесс деп аталады. Тепе-теңдңк процесс өте баяу өтуі тиіс, себебі параметрлердің өте тез өзгерісі кезінде газдың қысымы мен температурасы оның көлемінің барлық нүктелерінде сәйкес түрде бірдей мәндер қабылдап үлгере алмайды. Газдағы процесс аяқталған кезде газ жаңа күйге өтеді, ал оның параметрлері өздерінің бастапқы мәндерінен өзгеше болатын жаңа мәндерді қабылдайды. Егер тұрақты масса кезінде газдың барлық параметрлерінің мәндері процестің басында және ақырында бірдей болып шықса, онда процесс дөңгелек немесе тұйықталған процесс деп аталады. Қайсыбір праметрлердің процестің басындағы және ақырындағы мәндерінің арасындағы байланысты тағайындайтын қатынас газ зағы деп аталады. Газдың барлық үш параметрлерінің арасындағы байланысты өрнектейтін заң біріккен газ заңы деп аталады. Тағы бір айта кететін нәрсе, газдың бір ғана параметрі өзгеретін процесс кездеспейді, себебі барлық параметрлердің мәндері өзара байланысты болады. р және Т арасындағы байланысты өрнектейтін Шарль заңы осының мысалы бола алады.Қайтымды процесс деп екі бағытта да өте алатын процесті айтамыз, бірақ процесс әуелі бір бағытта өтіп, сонан кейін кері бағытта өткен болса, онда система, айналадағы денелерде қандай да бір өзгерістер болмастан, бастапқы күйіне оралуға тиіс.Қайтымды процеске мысал келтірейік. Абсолют серпімді ауыр шар көлбеу жазықтыққа А нүктесінде бекітулі тұрған болсын. Көлбеу жазықтық жиегіне қозғалмастай оған нормаль етіліп абсолют серпімді қабырға (қалқан) орнатылған делік. Егер шарды босатып жіберсек, ол көлбеу жазықтықтың бетімен домалап барып В қабырғасына соғылады да, ол қабырғадан серпіліп, қайтадан көлбеу жазықтықпен домалап, А нүктесіне келеді. Бұл жерде процесс бүтіндей қайталап отыр: айналадағы денелерде қандай да бір өзгерістер болмастан, шар қайтадан А нүктесіне оралды.

Жалпы алғанда, үйкеліссіз өтетін және серпімсіз соқтығысулар қатыспайтын нағыз механикалық процестердің барлығын да қайтымды процесс деп айтуымызға болады. Қайтымсыз процесс деп оған кері процесс анағұрлым күрделі процестің кезеңдерінің(буындарының) бірі ретінде ғана өте алатын процест айтады. Сөйтіп, қайтымсыз процестер үшін олардың қай бағытта өтетіндігінің үлкен мәні бар. Бір бағытта, оны біз “оң” бағыт деп айтатын боламыз, бұл процестер “өздігінен” өтеді, яғни тұйықталған системада өтіп отырған бірден-бір ғана процесс бола алады. Екінші, қарама-қарсы бағытта, оны біз “теріс” бағыт деп атайтын боламыз, ол процестер басқа “оң” процеспен селбесіп қана өте алады. Мысалы, жылудың ыстық денеден суық денеге көшуі (жылу өткізгіштік құбылысы) қайтымсыз процесс болып табылады. Денелердің температураларының теңелуіне келіп тірелетін бұл процесс те “өздігінен” өтеді, яғни тұйықталған системада өтетін бірден-бір процесс бола алады. Ал бұған кері “теріс” процесс- суық денеден жылудың ыстық денеге көшуі-“өздігінен” болмайды. Суытқыш машинаны пайдаланғанда жылу суығырақ денеден ыстығырақ денеге көшу үшін мұнымен қатар “оң” процестің өтуі қажет, бұл процесте А жұмыс істелініп, ол жұмыс қыздырғышқа берілетін ŋQ жылу мөлшеріне айналады.

25. Адиабаталық процесс. Пуассон теңдеуі.

Система мен оның айналасындағы денелер арасында жылу алмасуыболмаған жағдайда система күйінің өзгеруін адиабаталық өзгеріс деп атайды. Адиабаталық процесте система сырттан жылу алмайды және өзі де сыртқы денелерге жылу бермейді. Адиабаталық процесте система сырттан жылу алмайды және өзі де сыртқы денелерге жылу бермейді. Процесс адиабаталы түрде өту үшін система ешбір жылу өткізбейтін қабырғалармен қоршалған болу керек. Мұндай қабырғалар жасауға болмайтындықтан, әрбір нақты процесс адиабаталық процестерге азды-көпті жақын түрде ғана өтуі мүмкін. Практика жүзінде адиабаталық процестерге жақын процестер деп соншалықты шапшаң өтіп, сыртқы денелермен жылу алмасу ескерерліктей дәрежеге жете алмайтын процестерді айтуға болады.Газдың көлемі адиабаталық жағдайда өзгеретін болу үшін, жылу изоляциясы мейлінше (идеал) жақсы болуға тиіс; газдың жұмысы оның ішкі энергиясының есебінен орындалады; көлемі ұлғайғанда газ суиды да, сығылғанда қызады. Адиабаталық прцесс кезінде идеал газдың параметрлерін байланыстырып тұратын теңдеуді табайық. Термодиеамиканың бірінші бастамасының теңдеуіне идеал газ үшін dU өрнегін қоямыз:

d´Q_vdT+pdV

Адиабаталық процесс үшін d´ Q болғандықтан,

_vdT+pdV=0 (1)

Шарты орындалуы тиіс.

Енді p-ні идеал газдың күй теңдеуіне сәйкес V және Т арқылы анықтаймыз:

P=

Мұны (1) –ге қоямыз. Нәтижесінде нольден ерекше 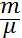көбейткішіне қысқартып, мынаны аламыз:

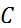_vdT+

Алынған өрнекті былайша түрлендіреміз:

Соңғы қатынасты

d(lnT+

түрінде жазуға болады, осыдан адиабаталық процесс кезінде

lnT+ =const (2)

екендігі шығады.

Идеал газ үшін С_р – С_v= Rекендігін ескерсек, R/C_v қатынасын γ – 1-мен алмастыруға болады, мұндағы γ=C_p/_v. (2) – де осындай түрлендіру жүргізіп және алынған шаманы потенцирлеп,

ТVγ^-1= const (3)

теңдеуіне келеміз. Табылған қатыс Т және V айнымалыларда идеал газдың адиабаталық теңдеуі болып табылады.Бұл теңдеуден идеал газдың теңдеуіне сәйкес Т-ні Р және V арқылы өрнектеп, р және V айнымалылары арқылы жазылған теңдеуге өтуге болады:

T=

Т-нің мәнін (3)- ке қойып және р және V шамаларының тұрақты екенін ескере отырып, мынаны аламыз: р Vγ=const^-1 (4)

(4) қатысы р және V айнымалылары арқылы жазылған идеал газ адиабатасының теңдпеуі болып табылады. Оны Пуассон теңдеуі деп те атайды.

Адиабатаның (4) теңдеуін изотерманың теңдеуімен салыстырудан адиабатаның изотермаға қарағанда тезірек өтетінін көреміз. Изотерма мен адиабата үшін 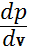– ның бір ғана (р, ) нүктедегі мәнін есептеп шығарайық.

Формуланы дифференциалдасақмына теңдеуді аламыз:

pdV + Vdp= 0

Осыдан изотерма үшін мынаны аламыз:

.

(4) – ті дифференциалдасақ былай болады:

pγV^γ-1dV+ V^γdp=0

Cонымен, адиобатаның көлбеу бұрышының тангенсі изотерманікінен γ есе артық болады екен.

Жоғарыда барлық уақыттарда да, газдың күйі әрбір мезетінде р және Т параметрлерінің белгілі мәндерімен сипатталады, яғни, басқа сөзбен айтқанда, қарастырылып отырған адиабаталық процесс тепе-теңдікте өтеді деп ұйғардық.Біз білетіндей, тек өте баяу өтетін процесс қана тепе-теңдіктегі процесс бола алады. Сонымен қатар табиғатта жылуды мүлдем өткізбейтін заттар болмайтындықтан, процесс неғұрлым аз уақытқа созылса, системның қоршаған ортамен алмасатын жылу мөлшері адиабаталық процесске жуық болады. Мұндай прцестің мысалына дыбыс толқыны таралған газдың әрбір нүктедегі сығылуы мен ұлғаюы жатады.Үлкен көлемнің шегінде бұл кездегі газ күйін тепе-теңдікте әрбір мейлінше аз көлем үшін газ күйі (4) адиабата теңдеуін толық қанағаттандырады.

Date: 2016-07-22; view: 2697; Нарушение авторских прав