Ламинарлық және турбуленттік ағыс. Үзіліссіздік теңдеуі. Бернулли теңдеуі

Сұйықтың ағысын ламинарлық және турбуленттік деп екіге бөледі. Сұйықтың жеке қабаттары бір-бірімен қарағанда параллель, яғни сұйық қабатта бір-бірімен араласпай қозғалатын болса, онда ағысты ламинарлық ағыс деп атайды. Сұйық бөлшектерінің жылдамдығы артып, шекті мәнге жеткенде әр қабаттардың бір-бірімен араласуы сұйықтың турбуленттік ағысы деп атайды.

Сұйықтың қалыптасқан ағыны кезінде сұйық сығылмайды деп есептесек, онда S₁ қимадан ағып өтетін сұйық көлемі қандай болса, S₂ қимадан ағып өтетін сұйық көлемі де дәл сондай болады, сондықтан 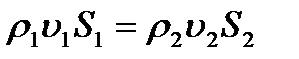(1)

Бұдан берілген сұйықтың сығылғыштығын ескермей оның тығыздығы ағын түтігінің барлық жерінде бірдей десек ( 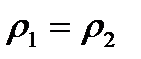), онда (1) өрнек мына түрде жазылады: (2)

немесе Sv=constСоңғы өрнектен сығылмайтын тұтқыр емес сұйық ағысының жылдамдығы мен ағын түтігінің көлденең қимасының көбейтіндісі берілген ағын түтігі үшін тұрақты шама болады. Бұл айтылған қорытынды ағынның үзіліссіздігі жөніндегі теорема деп аталады.(2) - теңдеуді мына түрде жазайық, яғни 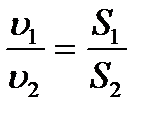Идеал сұйықтың қозғалысын (ағысын) сипаттайтын өрнекті 1738 жылы Д. Бернулли тұжырымдады. Бұл формуланы қорытып шығару үшін көлденең қималар әртүрлі түтікшедегі идеал сұйықтың қозғалысын қарастырган. Түтікшенің ішінен 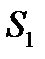және 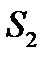аудандармен шектелген сұйық массасын алып, оның қозғалысын бақылаган. Сол аудандардағы ағын жылдамдықтары мен қысымдары , 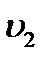және 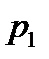, 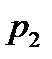болсын. Сұйықтық 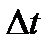уақыт аралығында жол жүріп,ал 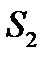қимада 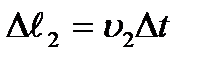жол жүреді. 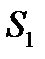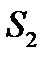Түтік белгілі-бір еңістікке ие және олардың және қималарының центрі берілген горизонтал деңгейден және 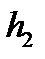биіктікте тұр.

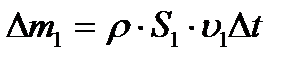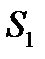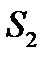және екенін ескеріп, бастапқыда және қималарының арасында орналасқан сұйық массасының толық энергиясының өзгерісін келесі түрде жазуға болады.

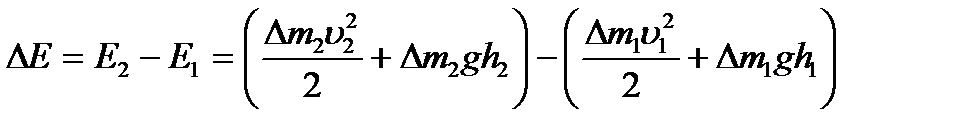
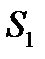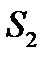Бұл өзгеріс, энергияның сақталу заңы бойынша сыртқы күштердің жұмысына негізделген. Берілген жағдайда сәйкес және қималарға әсер ететін қысым күштері 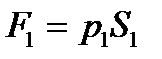және 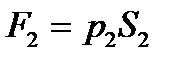, мұндағы 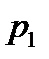және 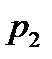- сәйкес қысымдар. 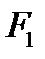күш пен 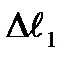орын ауыстырудың бағыттары бірдей, сондықтан 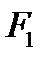күш оң жұмыс жасайды және 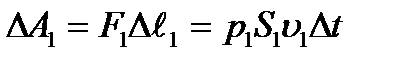-ға тең.

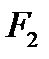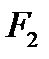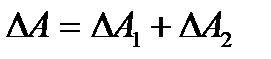қысым күші және орын ауыстырудың бағыттары қарама-қарсы. Олай болса, күш жұмысы теріс . Сонымен, сыртқы күш жұмыс жасайды.

Энергияның сақталу заңы бойынша қималар энергияларының айырымы сұйықты қозғалысқа келтіру үшін істелінетін жұмыстардың айырымына тең болады. Сыртқы күштердің қосынды жұмысы 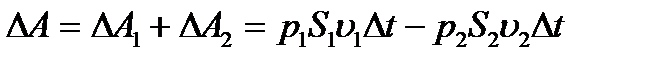- ға тең.

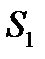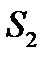уақыт ішінде және қималардан ағып өтетін сұйық көлемі 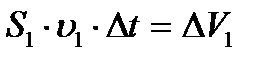және 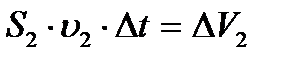үздіксіз теоремасы бойынша өзара тең 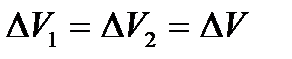. Сыртқы күштердің толық жұмысы

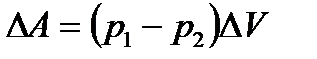
Кинетикалық энергияның өзгерісі жасалынған жұмысқа тең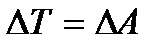

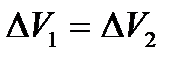теңдігінен және сұйықтың сығылмайтын шартынан

,

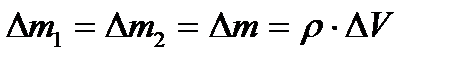мұндағы - сұйық тығыздығы, сондықтан өрнек келесі түрде жазылады.

соңғы өрнекті кез-келген түтік қималары үшін былай жазуға болады:

Бернулли теңдеуі деп аталады.

19.Сұйықтың тұтқырлығы. Стокс заңы.

Сұйықтың тұтқырлығы – сұйықтың қозғалысы барысында оның өз өңірінде үйкеліс күшін тудыру қабілеті. Тұтқырлық - сұйықтар мен газдардың негізгі қасиеттерінің бірі. Мысалы, машиналарды майлау үшін жанармайды алдын ала тұтқырлығына қарап таңдап алады. Сұйық тұтқырлығының температураға байланыстылығын өте күшті болады. Себебі сұйықтың температурасы жоғарылап кризистік температураға жеткенде (мысалы, суды алсақ ол 1000с-та қайнап буға айналады) басқа фазаға өтеді. Әсіресе майлар тұтқырлығының тәуелділігі күшті, мысалы, температурасы 180 С-тан 400 С-қа дейін көтерілгенде кастор майының тұтқырлығы төрт еседей кемиді.Барлық нақты сұйықтардың бір қабаты екінші қабатымен салыстырғанда орын ауыстырса, онда азды-көпті үйкеліс күші пайда болады. Шапшаңырақ қозғалатын қабат тарапынан жай қозғалатын қабатқа үдетуші күш әсер етеді. Керісінше, жай қозғалатын қабат тарапынан шапшаң қозғалатын қабатқа бөгеуші күш әсер етеді. Бұл күштер ішкі үйкеліс күштері деп аталады, олар қабаттардың бетіне жүргізілген жанама бойымен бағытталады. Ішкі үйкеліс күшінің шамасы сұйық ағысының v жылдамдығы бір қабаттан екінші қабатқа көшкенде қаншалықты шапшаң өзгеретіндігіне тәуелді және қарастырылып отырған сұйық қабаты бетінің S ауданы неғұрлым үлкен болса, соғұрлым зор болады. Мысалы, бірінен-бірі Δh қашықтықтағы сұйықтың екі қабаты v1 және v2 жылдамдықпен ақсын (v1- v2=Δv) делік. Қабаттардың Δh арақашықтығын өлшегенде бағыт сол қабаттардың ағыс жылдамдығына перпендикуляр болсын. Сонда Δv/Δh шамасы бір қабаттан екінші қабатқа көшкенде жылдамдықтың қаншалықты шапшаң өзгеретіндігін көрсетеді, оны жылдамдық градиенті деп атайды. Ньютон алғаш рет сұйықтың екі қабатының арасындағы үйкеліс күші жылдамдықтар айырымы мен жанасып тұрған сұйық қабаттары бетінің ауданына тура пропорционал және сол қабаттардың ара қашықтығына кері пропорционал екендігін дәлелдеді.

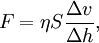
мұндағы η-пропорционал коэффициент, яғни сұйықтың тұтқырлық коэффициенті деп аталады.

Тұтқырлық коэффициенті неғұрлым үлкен болған сайын сұйықтың идеал сұйықтан айырмашылығы мен үйкеліс күші соғұрлым үлкен болады. Егер екі сұйық қабаты шексіз жақын болса, онда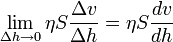

Сұйық тұтқырлығының әсерінен болатын қозғалыс кезіндегі жанама кернеулігі мынадай:

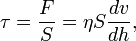
сұйықтың тұтқырлық коэффициенті:

Тұтқырлық коэффициенттің өлшемділігі: η=ML-1T-1

Тұтқырлық динамикалық коэффициенті 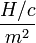-пен өлшенеді, яғни жылдамдық градиенті - 1 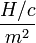. Бетінің ауданы 1 м2 сұйық қабаттарының әсерлесу кезіндегі тұтқырлық күші 1 Н болады. Әдетте η коэффициентін тұтқырлықтың абсолюттік коэффициенті деп атайды. Ал осы коэффициенттің берілген сұйықтың тығыздығына (ρ) қатынасы тұтқырлықтың кинетикалық коэффициенті делінеді, ол

Бұл тұтқырлық коэффициентіне кері шама, яғни 1/η - аққыштық коэффициенті деп аталады.

Тұтқырлықтың әсері ағынның қозғалмайтын денемен өзара әсерлесуі кезінде де байқалады.Тұтқырлығы сұйық ішіндегі радиусы ,жылдамдығы 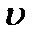шар қозғалысына жасалатын кедергі күші мынаған тең:

,

Бұл өрнек Стокс теңдеуі деп аталады. Стокс өрнегі лабораториялық практикум сабағында сұйықтардың 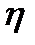тұтқырлық коэффициентін анықтау үшін қолданылады. Стокс тағайындаған заң бойынша: кедергі күші бірінші дәрежеде алынған жылдамдыққа, тұтқырлық коэффициентіне және дененің сызықтық өлшемдеріне тура пропорционал болады.

Date: 2016-07-22; view: 3015; Нарушение авторских прав