Жылдамдық қозғалыстың шапшаңдығын, берілген уақыт мезетіндегі бағытын сипаттайтын векторлық шама.

Жылдамдық − радиус-вектордың уақыт бойынша туындысы:

Орташа жылдамдық – скаляр шама. Орташа жылдамдық t ғана емес, сонымен қатар Δt-ға да байланысты.

Материалдық нүкте қозғалысы әр уақыт мезетінде, яғни басқаша айтқанда траекторияның әр нүктесінделездік жылдамдық деген физикалық шамамен сипатталады. Енді t уақыт мезетін өзгерпей, ал Δt уақыт аралығын азайта отырып нольге ұмтылдырамыз. Сонда Δx жол аралығында нольге ұмтылады. -ға қатынасы тəжірибенің көрсетуі бойынша белгілі бір шекке ұмтылады, ол тек қана

t-ға байланысты, бірақ Δt-ға байланысты болмайды. Осы шек t уақыт мезетіндегі

материалдық нүктенің лездік жылдамдығы деп аталады:

Бұл формула бойынша анықталатын шек х-тің уақыт бойынша туындысы деп те аталады:

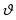лездік жылдамдық деп, х-тың уақыт бойынша туындысы немесе жүріп өткен жолдың уақыт бойынша туындысы:

Лездік жылдамдық векторлық шама, ол қозғалыс траекториясына жүргізілген жанама бойымен бағытталған. Вектор болғандықтан жылд–тың біріңғай бағыты немесе біріңғай модулі ғана өзгеріп қоймай, әрі бағыты, әрі модулі бір мезгілде өзгеруі мүмкін.

1.Механикалық қозғалыс. Механикалық жүйе. Механиканың негізгі моделі: материалдық нүкте, қатты дене, тұтас орта.

Механикалық қозғалыс деп уақыт өзгерісінде кеңістікте дененің басқа денелерге қатысты орын ауыстыруын айтамыз.

Механикалық қозғалыс – салыстырмалы. Бір дененің әр түрлі денелерге қатысты қозғалысы әр түрлі болады. Дененің қозғалысын сипаттау үшін қозғалыс қай денеге қатысты қарастырылатынын белгілеу қажет. Бұл денені санақ денесі деп атайды. Санақ денесі және уақыт – санақ жүйесін құрап, ол қозғалған дененің кез келген уақыттағы орнын анықтауға мүмкіндік береді.

Тек механикалық процестер өтетін жүйелер механикалық жүйе деп аталады. Тұйықталған механикалық жүйеде потенциалдық және кинетикалық энергиялардың қосындысы тұрақты шама болып қалады (мұндай жүйелер консервативтік деп аталады).

Дененің еркін түсуі кезінде кез келген уақыт мезетінде оның кинетикалық және потенциалдық энергиясының қосындысы тұрақты болатынын ескеру керек.

Әрбір дене белгілі бір өлшемдерге ие. Дененің әр түрлі бөліктері кеңістіктің әр түрлі жерлерінде орналасады. Берілген есептің шартында дененің өлшемі мен формасын ескермеуге

болатын денені материалдық нүкте деп атайды. Мәселен, оны ғаламшарлардың Күннің айналасындағы қозғалысын зерттегенде алуға болады. Бұл нәрсе деформацияланбайды, айнала алмайды. Материалдық нүктенің механикалық энергиясы тек қана оның кинетикалық энергиясы түрінде ғана жинақтала алады. Басқаша айтқанда, материалдық нүкте ең қарапайым механикалық жүйе; ең аз еркіндік дәрежесі бар механикалық жүйе.

Абсолют қатты дене – ешбір жағдайларда да деформацияланбайтын дене және барлық жағдайларда да бұл дененің екі нүктесінің немесе екі бөлшегінің арақашықтығы өзгеріссіз қалады.

­Өзгермелі тұтас орта – қатты денелердің, сұйықтықтар мен газдардың қозғалысын зерттегенде олардың молекулалық құрылымын ескермеуге болатын жағдайда қолданылатын ұғым.

2.Механиканың негізгі ұғымдары: радиус-вектор, траектория, орын ауыстыру, жол.

Механикалық қозғалыс деп уақыт өзгеруіне байланысты денелердің кеңістікте орын ауыстыруын айтады. Денелердің кеңістікте орын ауыстыруын басқа бір денемен немесе денелер жүйесімен салыстырып анықтай аламыз.

Ондай денені немесе денелер жүйесін санақ жүйесі деп атайды. Дененің кеңістіктегі орнын анықтау үшін декарттық координаттар жүйесін алады. Дененің қозғалысын радиус-вектор арқылы да анықтауға болады. Нүктенің радиус-векторы деп координата басынан берілген нүктеге жүргізілген векторды айтамыз.

Уақыт өткенде бір нүктеден екінші нүктеге орын ауыстырғанда, дене (материалдық нүкте) дене қозғалысының траекториясы деп аталатын қандай да бір қисықты сызады.

Дененің кез келген уақыттағы кеңістікте орнын (қозғалыс заңын) x = x (t), y = y (t), z = z (t) координаттардың уақыттан тәуелділігінен (координаттық әдіс) не болмаса уақыттың бастапқы нүктеден берілген нүктеге жүргізілген радиус-вектордан тәуелділігінен (векторлық әдіс) анықтауға болады.

Дененің орын ауыстыруы деп дененің бастапқы орнын оның кейінгі орнымен қосатын бағытталған кесіндіні айтады. Орын ауыстыру – векторлық шама.

Жүрген жолы - дененің белгілі t уақыттың ішінде траектория доғасының ұзындығына тең болады. Жол – скалярлық шама.

Егер дененің қозғалысын жеткілікті аз уақыттың ішінде қарастырса, онда орын ауыстыру векторы осы нүктеге жүргізілген траекторияның жанамасы бойымен бағытталады, ал оның ұзындығы жүрілген жолына тең болады.

3.Механиканың негізгі ұғымдары: жылдамдық, орташа жəне лездік жылдамдық.

Жылдамдық – механиканың негізгі заңдарын тұжырымдайтын физикалық шама.

Нүкте қозғалысының жылдамдығы - нүктенің орын ауыстыруының осы орын ауыстыру өткен уақыт аралығына қатынасымен анықталатын нүкте қозғалысының сипаттамасы.

Δх жүрілген жолдың Δt уақыт аралығында қатынасын немесе, дəлірек, t жəне t+Δt уақыт аралығындағы қатынасын материалдық нүктенің орташа жылдамдығы деп атаймыз. Сонымен, анықтамасы бойынша орташа жылдамдық мынаған тең:

_орт

Орташа жылдамдық – скаляр шама. Орташа жылдамдық t ғана емес, сонымен қатар Δt-ға да байланысты.

Материалдық нүкте қозғалысы әр уақыт мезетінде, яғни басқаша айтқанда траекторияның әр нүктесінделездік жылдамдық деген физикалық шамамен сипатталады. Енді t уақыт мезетін өзгерпей, ал Δt уақыт аралығын азайта отырып нольге ұмтылдырамыз. Сонда Δx жол аралығында нольге ұмтылады. -ға қатынасы тəжірибенің көрсетуі бойынша белгілі бір шекке ұмтылады, ол тек қана

t-ға байланысты, бірақ Δt-ға байланысты болмайды. Осы шек t уақыт мезетіндегі

материалдық нүктенің лездік жылдамдығы деп аталады:

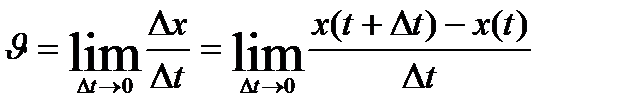
Бұл формула бойынша анықталатын шек х-тің уақыт бойынша туындысы деп те аталады:

лездік жылдамдық деп, х-тың уақыт бойынша туындысы немесе жүріп өткен жолдың уақыт бойынша туындысы:

Лездік жылдамдық векторлық шама, ол қозғалыс траекториясына жүргізілген жанама бойымен бағытталған. Вектор болғандықтан жылд–тың біріңғай бағыты немесе біріңғай модулі ғана өзгеріп қоймай, әрі бағыты, әрі модулі бір мезгілде өзгеруі мүмкін.

4. Үдеу. Үдеудің нормал жəне тангенциал құраушылары. Толық үдеу.

Дененің лездік үдеуі (немесе үдеу) деп жылдамдықтың аз өзгеруінің сол жылдамдық өзгерген уақыттың аз өзгеруіне Δt қатынасының шегін айтамыз.

Қисық сызықты қозғалыс кезінде үдеу векторының бағыты жылдамдық векторының бағытымен сәйкес келмейді. үдеу векторының құраушыларын жанама (тангенциал) және нормаль үдеу деп атайды (сурет 1.1.5).

Сурет 1.1.5. Жанама және нормаль үдеулер.

Жанама үдеу дененің жылдамдығы модуль жағынан қалай өзгеретінін көрсетеді:

векторы траекторияға жанама бойымен бағытталады.

Нормаль үдеу дененің жылдамдығы бағыты жағынан қалай өзгеретінін көрсетеді. Қисық сызықты қозғалысты шеңберлер доғаларының бойымен қозғалыс түрінде көрсетуге болады (сурет 1.1.6).

Сурет 1.1.6 Шеңберлер доғаларының бойымен қозғалыс.

Нормаль үдеу v жылдамдықтың модулінен және дене осы уақытта қозғалған шеңбердің R радиусынан тәуелді.

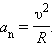
векторы әрқашан шеңбердің центріне бағытталады.

1.1.5. суретінен толық үдеудің модулі

шамасына тең болатыны көрініп тұр.

Сонымен, кинематикада материалдық нүктенің негізгі физикалық шамаларының қатарына: l жүрген жолы, Δs орын ауыстыруы, жылдамдық және үдеу жатады. l жолы – скаляр шама болып табылады. Δs орын ауыстыруы, жылдамдығы және үдеу – векторлық шамаларға жатады. Векторлық шаманы көрсету үшін, оның модулін және бағытын көрсету қажет. Векторлық шамалар белгілі математикалық ережелерге бағынады. Векторларды координата осьтеріне проекциялауға, оларды қосуға, алуға, т.с.с. болады.

5. Қисық сызықты қозғалыстағы жылдамдық жəне үдеу.

Егер материалдық нүкте қозғалғанда оның траекториясы қисық сызық болып келсе, онда қозғалыс қисық сызықты қозғалыс деп аталады. Енді осы қисық сызықты қозғалыс кезіндегі жылдамдықпен үдеудің өзгерісін қарастырайық.

Қисық сызықты қозғалыс кезінде жылдамдық векторы берілген әрбір уақыт мезетінде дене траекториясына қозғалыстың бағыты бойынша жүргізілген жанама бойымен бағытталады. Дененің MN қисық сызығының бойымен қозғалысын қарастырайық.(4-сурет).

Айталық M және N нүктелеріндегі қозғалыс жылдамдықтары және болсын. Ал M нүктесіндегі үдеу (1.2.9) өрнекке сәйкес мына шамаға тең.

(1.3.1)

4 – суретте көрсетілгендей бойына -ға тең 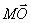және кесінділерін аламыз. Сонда үдеуді былайша өрнектейміз:

(1.3.2)

(1.3.2)- өрнектің екінші құраушысы жанама немесе тангенциал үдеу деп аталады, себебі Δt→0 кезде OD кесіндісі M нүктесінің маңында айналып, траекторияның жанамасымен беттесуге ұмтылады. Оның сан мәні мынаған тең: (1.3.3)

Сонымен үдеу қозғалыс жылдамдығының сан жағынан өзгерісін көрсетеді. Кез келген бірқалыпты қозғалыс үшін 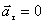болады. Ал (1.3.2)- өрнектің бірінші құраушысы нормаль немесе центрге тартқыш үдеу деп аталады, себебі Δt→0 кезде Δt→0 да, M нүктесіндегі 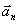жанамаға перпендикуляр болады. Сөйтіп, нормаль үдеудің сан мәні мына шамаға тең:

Енді ВО кесіндісінің мәні неге тең болатынын қарастырайық. ΔМВО-дан Δα бұрышын шексіз аз шама деп есептесек, ВО=MB Δα=vΔα, өйткені . Сонымен нормаль үдеуді мына түрде жазуға болады: Бұл өрнектің оң жағын Δs–ке көбейтіп және бөлейік, сонда ол түрге келеді. Мұндағы Δs – MN доғасының ұзындығы. Егер геометрия курсынан қисық сызықтың қисықтығы деген ұғымды еске алатын болсақ, онда 4-суретке сәйкес Δs=RΔα. мұндағы R -қисықтық радиусы, Δα - центрлік бұрыш. Олай болса, Δα/ Δs=1/R және M нүктесіндегі жылдамдық Δt уақыт өзгерісіне тәуелді болмайды.

Сөйтіп (1.3.4)

Сонымен, қисық сызықты қозғалыс кезінде нормаль үдеу қозғалыс жылдамдығы бағытының өзгерісін көрсетеді. Кез келген түзу сызықты қозғалыс үшін . теңдіктен материалдық нүктенің қисық сызықты қозғалысы кезіндегі толық үдеуі оның нормаль және тангенциал үдеулері векторларының қосындысына тең екендігін көреміз: Толық үдеудің бағытын тангенциал үдеу мен толық үдеу немесе нормаль үдеу мен толық үдеу арасындағы бұрыш арқылы көрсетуге болады: 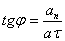(1.3.6)

6. Айналмалы қозғалыс. Бұрыштық жылдамдық жəне бұрыштық үдеу.

Шеңбер бойымен қозғалыс. Дененің шеңбер бойымен қозғалысы қисық сызықты қозғалыстың дербес жағдайы болып табылады. орын ауыстыру векторымен қатар радианмен өлшенетін бұрыштық орын ауыстыруын қарастыру ыңғайлы. Доғаның ұзындығы бұрылу бұрышымен Δl = RΔφ. қатынаспен байланысты. Бұрылу бұрышы аз болған кезде Δl ≈ Δs.

.-сурет. Дененің шеңбер бойымен сызықты және бұрыштық орын ауыстыруы.

Шеңбер траекториясының берілген нүктесіндегі бұрыштық жылдамдық деп кішкентай бұрыштық орын ауыстыруының кішкентай уақыт аралығына қатынасының шегін айтады.

Бұрыштық жылдамдық рад/с өлшенеді. Сызықтық жылдамдығы мен бұрыштық жылдамдығының арасындағы байланыс υ = ωR. Дененің шеңбер бойымен бірқалыпты қозғалыс кезінде υ және ω шамалары тұрақты болады. Бұл жағдайда векторының бағыты ғана өзгереді.

Дененің шеңбер бойымен бірқалыпты қозғалысы үдемелі қозғалыс болып табылады.

Айналыс бір қалыпты болмаған жағдайда бұрыштық жылдамдық ω уақытқа байланысты өзгереді. Осындай өзгерісті сипаттау үшін бұрыштық үдеу (β)деген ұғым енгізіледі. Бірқалыпты айнымалы айналма қозғалыстың бұрыштық үдеуі дегеніміз бұрыштық жылдамдықтың өзгерісіне тура пропорционал және осы өзгеріс болуына кеткен уақыт аралығына кері пропорционал болып келген физикалық шама (β) болады. Бұрыштық үдеу — бұрыштық жылдамдықтың өзгеру шапшаңдығын сипаттайтын векторлық шама; - бұрыштық жылдамдық өзгерісінің осы өзгеріс өткен уақыт аралығына қатынасымен анықталатын бұрыштық жылдамдықтың өзгеруінің лездігі. Бұрыштық үдеудің бірліктердің халықаралық жүйесіндегі бірлігі: рад/с2. Айналыс бір қалыпты болмаған жалпы жағдайда, берілген уақыт кезеңіндегі бұрыштық үдеу мынаған тең: Дифференциалдық есептеуден: сонда бұрыштық үдеу:

7. Механикадағы күштер: ауырлық күші жəне дененің салмағы.

Жердің тартылыс күші әсерінен барлық денелер Жер бетіне қатысты бірдей үдеумен түседі. Оның g әрпімен белгілеу қабылданған. Мұның өзі Жермен байланысты санақ системасындағы массасы m кез келген денеге ауырлық күші деп аталатын P = mg күштің әсер ететінін көрсетеді. Дене Жер бетіне қатысты тыныштықта тұрғанында, Р күші денені құлатпай ұстап тұрған ілменің немесе тіреуіштің fr реакциясымен теңгеріліп тұрады. Ньютонның үшінші заңы бойынша дене бұл жағдайда ілмеге немесе тіреуішке - fr – ге тең G күшпен әсер етеді, яғни G = P = mg

Дененің ілмеге немесе тіреуішке әсер ететін G күші дененің салмағы делінеді. Дене мен тіреуіш н-се жерге қатысты қозғалмай тұрған жағдайда ғана бұл күш mg-ге тең болады.Олардың қандай да болсын w үдеумен қозғалған жағдайында G күші mg тең болмайды.Мысалы,ілме рамаға бекітілген пружин түрінде w үдеуі бар денеменбірге қозғалсын делік.Сонда дене қозғалысыныңтеңдеуі мына түрге келеді: P+ fr=mw, бұдан мына формула шығады G = m(g-w).

Дененің массаыс мен салмағының арасындағы қатыс өлшеу арқылы алынған дене массаларының салыстырмалы тәсілін береді, яғни бұл тәсіл бойынша бірдей жағдайда (әдетте w=0) жер бетінің бір нүктесінде анықталған дене салмақтарының қатынастары осы денелердің массаларының қатынасына теі болады, яғни : : :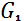

8.Серпімділік күші. Гук заңы. Дененің деформациясы кезінде, дененің бастапқы қалпын мен өлшемін сақтайтын кері күш пайда болады. Бұл күш атом және молекула арасында электромагниттік әсерлесу кезінде пайда болады. Мұндай күшті серпімділік күші деп атайды. Деформацияның қарапайым түрі – созылу және сығылу деформациясы болып табылады (1.12.1-сурет).

1.-сурет. Созылу (x > 0) және сығылу (x < 0) деформациялары. Сыртқы күш . Кіші деформация кезінде (|x| << l) серпімділік күші дененің деформациясына пропорционал және деформация кезіндегі дене бөлшектерінің орын ауыстыруына қарама-қарсы бағытталады.

Fx = Fупр = –kx. Бұл қатынас экспериментальды қойылған Гук заңын береді. k коэффициентін дененің қатаңдығы деп атайды. СИ жүйесінде қатаңдық ньютон метрге (Н/м) өлшенеді. Қатаңдық коэффициенті дененің қалпы мен мөлшеріне және дене жасалған материалына байланысты. Физикада Гук заңын тартылу және сығылу деформациясын басқа түрде жазады. ε = x / l қатыстық деформация, ал σ = F / S = –Fупр / S, мұндағы S – деформацияланған дененің көлденең қимасының ауданы кернеудеп аталады. Онда Гук заңын қатыстық деформацияε, σ кернеуге пропорционал болады.

E коэффициенті Юнг модулідеп аталады. Юнг модулі тек дененің жасалған материалына байланысты, ал дененің қалпы мен өлшемінен тәуелсіз. Әр түрлі материалдар үшін Юнг модулі кең аралықтарда өзгереді. Мысалы, болат үшін E ≈ 2·1011 Н/м2, ал резина үшін E ≈ 2·106 Н/м2, яғни 5 ретке кемиді. Гук заңы күрделі деформациялар үшін жалпылануы мүмкін. Мысалы, иілу деформациясы кезінде серпімділік күші ұштары екі тіреуде орналасқан стерженнің иілуіне пропорционал (1.12.2сурет)

.12.2.сурет. Иілу деформациясы . серпімділік күші тіреу тарапынан денеге әсер ететін күшті тіреудің реакция күші деп аталады. Жанасқан кезде денелердің реакция күші жанасқан бетке перпендикуляр бағытталады. Сондықтан нормаль қысым күші деп атайды. Егер дене қозғалмайтын горизонталь үстелдің үстінде жатса, онда тіреу күші вертикаль жоғары бағытталған және ауырлық күшіне теңгеріледі. .Мұндағы үстелге әсер ететін күші дене салмағы деп аталады. Техникада көбінесе спираль тәрізді серіппе қолданылады (1.12.3-сурет). Серіппенің созылу немесе сығылу кезінде Гук заңына бағынатын серпімділік күші пайда болады. k коэффициенті серіппенің қатаңдығы деп аталады. Гук заңының қолданылған кезде серіппенің ұзындығының өзгеруі ықтимал. Сондықтан оларды күшті өлшеуге қолданылады. Күш бірліктеріне бөлінген созылуға арналған серіппені динамометр деп атайды. Мұндағы ескерту: созылу және сығылу кезіндегі серіппенің орамдарында айналу және иілу сияқты күрделі деформациялар болады.

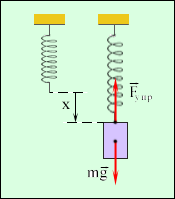
.12.3 сурет. Серіппенің созылу деформациясы. Серіппеге қарағанда кейбір созылғыш материалдарды (резина) созылу және сығылу немесе серіппелі стерженьдердің сығылуы (немесе сым) сызықты Гук заңына өте тар ауқымда бағынады. Металдар үшін ε = x / l қатыстық деформациясы 1 %-тен аспауы тиіс. Үлкен деформациялар кезінде қайтымсыз құбылыстар немесе материалдың бұзылуына әкеледі.

9. Үйкеліс күші. Бүкіл әлемдік тартылыс заңы. Үйкеліс күщі екі дененің жанасу кезінде пайда болады. Басқа заңдар сияқты, үйкеліс күші де Ньютонның үшінші заңына бағынады: егер бір денеге үйкеліс күші әсер етсе, онда модулі бойынша осындай, бірақ қарама-қарсы бағытталған күш екінші денеде пайда болады. Үйкеліс күші басқа күштер сияқты электромагниттік болады. Олар өзара жанасқан денелердің атомдары мен молекулаларының арасында пайда болады.

Құрғақ үйкеліс күші деп қатты денелердің арасында сұйық және газ тәрізді қабаттың болмаған кездегі әсерлесуін айтады. Олар әсерлескен беттерге әр уақытта жанама бойымен бағытталады.

Дененің тыныштық кезінде пайда болған құрғақ үйкелісін тыныштық үйкелісі деп атайды. Тыныштық үйкеліс күші шамасы жағынан қарама-қарсы бағыттылған (1.13.1 суреті)

.1 сурет. Тыныштық үйкеліс күші (U=0). Тыныштық үйкеліс күші қандай да бір максималды (Fтр)max мәннен аспайды. Егер сыртқы күш (Fтр)max-ден үлкен болса, онда қатыстық сырғанау пайда болады. Бұл жағдайда үйкеліс күшін сырғанау үйкеліс күші деп атайды. Ол әрқашан қозғалыс бағытына қарама-қарсы бағытталады және жалпы жағдайда дененің қатыстық жылдамдығына байланысты. Бірақта, көп жағдайда сырғанау үйкеліс күші жуық шамамен денелердің қатыстық жылдамдықтарына тәуелсіз максималды тыныштық үйкеліс күшіне тең. Бұл құрғақ үйкеліс күші көптеген қарапайым физикалық есептерді шығаруда қолданады

Тәжірибеден сырғанау үйкеліс күші денненің тіреуге әсер ететін нормаль күшіне пропорционал, ал бұдан реакция күшіне тең екендігі шығады.

пропорционалдық коэффициентін сырғанау үйкелісінің коэффициенті деп атайды.

коэффициенті - өлшемсіз шама. Әдетте үйкеліс коэффициенті бірден кіші. Ол жанасатын денелердің материалына және бетінің өңдеу сапасына байланысты. Сырғанау кезінде үйкеліс күші бағыты жанама бойымен бағытталады, ал қатыстық жылдамдыққа қарама-қарсы бағытталады.(1.13.3 сурет)

. 13.3 сурет. Сырғанау кезіндегі үйкеліс күші .- тіреудің реакция күші. - ден салмағы.

қатты дененің сұйықтықта немесе газда қозғалысы кезінде тұтқырлы үйкеліс күші пайда болады. Тұтқырлы үйкеліс күші құрғақ үйкеліс күшінен біршама төмен болады. ол да қатыстық жылдамдыққа байланысты қарама-қарсы бағытталған. Тұтқырлы үйкеліс күші кезінде тыныштық үйкелісі болмайды. Тұтқырлы үйкеліс күші дененің жылдамдығына қатты тәуелді болады. Жеткілікті аз жылдамдықта Fтр ~ υ, ал үлкен жылдамдықта Fтр ~ υ2. Мұндағы пропорционалды коэфициенттер дененің қалпына тәуелді болады. Үйкеліс күші денені тербеткенде пайда болады. Әдетте тербету үйкеліс күші жеткілікті аз болады. Қарапайым есептерді шешкен кезде мұны көбінесе ескермейді. Бүкіл әлемдік тартылыс заңы. Бүкіл әлемдік тартылыс заңын 1682 жылы И. Ньютон ашты. 1665 жылдың өзінде 23 жасар Ньютон Айды орбитада ұстап тұрған күштер мен алманың Жерге құлауын тудыратын күштердің табиғаты бірдей деп айтты. Оның гипотезасы бойынша әлемнің барлық денелерініңарасында массалар центрлерін қосатын сызық бойымен бағытталған тартылыс (гравитациялық) күштер әсер етеді (1.10.1-сурет).

. 10.1-сурет. Денелер арасындағы гравитациялық тартылыс күштер. Біртекті шар түріндегі дененің массалар центрі оның центрімен беттеседі. Кейінгі жылдары Ньютон XVII ғасырда И. Кеплер ашқан ғаламшарлардың қозғалыс заңдарының физикалық тұрғыдан түсіндіруге тырысты. Ғаламшарлардың қалай қозғалатынын біле отырып, Ньютон оларға қандай күштер әсер ететінін анықтамақшы болды. Мұндай жол механиканың кері есебі атына ие. Егер механиканың негізгі есебі – белгілі массаның координаталарын және кез келген уақыттағы белгілі күштер арқылы жылдамдықтарын анықтау болса (механиканың тура есебі), онда кері есепті шығарған кезде оның қалай қозғалатыны белгілі болған жағдайда оған әсер ететін күштерді анықтау қажет. Осы есепті шығару Ньютонды бүкіл әлемдік тартылыс заңын ашуға әкелді.

Барлық денелер массаларына тура пропорционал, және олардың арақашықтығының квадратына кері пропорционал күшпен тартылады.

Пропорционалдық коэффициент G табиғаттағы барлық денелер үшін бірдей. Оны гравитациялық тұрақты деп атайды.: G = 6,67·10^–11 Н·м²/кг² (СИ).

Табиғаттағы көптеген құбылыстар бүкіл әлемдік тартылыс заңымен түсіндіріледі. Ғаламшарлардың Күн жүйесінде қозғалысы, Жердің жасанды серіктерінің қозғалысы, баллистикалық ракеталарының ұшу траекториясы, Жердің бетіне жақын денелердің қозғалысы – осы құбылыстардың барлығы бүкіл әлемдік тартылыс заңы және динамиканың заңдарымен түсіндіріледі.

10.Қысым.Архимед күші. Сұйық денелердің қатты (серпімді) денелерден басты айырмашылығы – бұл олардың өзінің формасын жеңіл өзгертуі. Сұйық бөліктері бірінің үстіне бірі сырғанап, еркін қозғала алады. Сондықтан сұйық өзі құйылған ыдыстың формасын жеңіл алады. Сұйықтарға да, газдарға да қатты денелерді батыруға болады. Газдарға қарағанда, сұйықтар сығылмайды. Сұйыққа немесе газға батырылған денеге дененің бетіне үлестірілген күштер әсер етеді. Осындай үлестірілген күштерді сипаттау үшін, жаңа физикалық шама – қысым енгізіледі. Қысым – бетке перпендикуляр әсер ететін күштің модулінің осы беттің ауданына қатынасымен анықталады:

СИ жүйесінде қысым паскальмен (Па) өлшенеді. 1 Па = 1 Н/м2. Өте жиі жүйелік емес бірліктер – қалыпты атмосфера (атм), сынап бағанасының миллиметрі (мм Hg) пайдаланады: 1 атм = 101325 Па = 760 мм Hg. Сұйықтың әр түрлі деңгейдегі қысымдардың айырымынан итеріп шығаратын немесе архимед күші пайда болады.

.15.3.-суретте архимед күшінің пайда болуы суреттелген. Сұйыққа биіктігі h, табанының ауданы S болатын тік бұрышты параллепипед батырылған. Төменгі және жоғарғы қырының қысымдарының айырымы:Δp = p2 – p1 = ρgh. Сондықтан итергіш күші жоғары бағытталып, оның модулі:FA = F2 – F1 = SΔp = ρgSh = ρgV

болады, мұндағы V – сұйық итеріп шығарған дененің көлемі, ρV – оның массасы. Сұйыққа немесе газға батырылған архимед күші дене ығыстырып шығарған сұйықтың немесе газдың көлеміне тең болады. Бұл тұжырым Архимед заңы деп аталып, кез келген пішінді денелер үшін орындалады.

1.15.3.-сурет.Архимедкүші. FA = F2 – F1 = S(p2 – p1) = ρgSh, F1 = p1S, F2 = p2S.

Архимед заңынан: егер дененің орташа тығыздығы ρд сұйықтың (газдың) тығыздығынан ρ үлкен болса, онда дене ыдыстың түбіне түседі. Егер ρд < ρ болса, онда дене сұйық бетінде қалқып жүреді. Дененің батырылған бөлігінің көлемі сұйық итеріп шығарған салмағы дененің салмағына тең болады. Ауа шарын ауада көтеру үшін, оның салмағы итеріп шығарылған ауаның салмағынан кіші болу қажет. Сондықтан ауа шарын жеңіл газдармен (сутегімен, гелиймен) және қыздырылған ауамен толтырады. Сұйықтағы толық қысым өрнегінен p = p0 + ρgh біртекті сұйықпен толтырылған кез келген пішінді байланысқан ыдыстарда бір деңгейдегі кез келген нүктеде қысымдар бірдей болады (1.15.4-сурет).

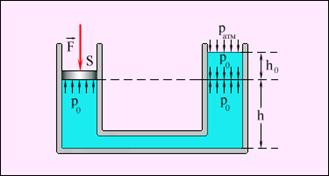15.4-сурет. Байланысқан ыдыстардың мысалы. Оң ыдыста сұйықтың беті бос. h деңгейінде екі ыдыста да қысым бірдей және p0 = F / S = ρgh0 + pатм шамасына тең. Ыдыстардың түбіне p = p0 + ρgh қысым түседі.Егер өзара байланысқан вертикаль орналастырылған цилиндрлерді поршеньдермен жауып қойса, онда поршеньдерге салынған сыртқы күштердің көмегімен үлкен р қысымын тудырып, ол жүйенің осы нүктесіндегі ρgh гидростатикалық қысымынан бірнеше есе көп болады. Онда бүкіл жүйеде бірдей р қысымы болады деп есептеуге болады. Егер поршеньдердің аудандары S1 және S2 әр түрлі болса, онда оларға сұйықтың тарапынан әр түрлі күштер әсер етеді: F1 = pS1 и F2 = pS2. Жүйені тепе-теңдікте ұстау үшін. модульдері жағынан тең, бірақ бағыты жағынан қарама-қарсы сыртқы күштер түсірілуі қажет. Сонымен:

Егер S2 >> S1, онда F2 >> F1. Мұндай типтегі құралдарды гидростатикалық машина деп атайды (1.15.5.-сурет). Олар күште үлкен ұтыс алуға көмектеседі. Егер тар цилиндрдегі поршеньді сыртқы күштің әсерімен қашықтыққа көшірсе, онда кең цилиндрдегі поршень ауыр жүкті көтеріп,

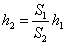қашықтыққа көшіріледі. Сонымен күш ұтысы да, жолы ұтылысы да есе өзгереді. Сонымен бірге, күштің ара қашықтыққа көбейтіндісі тұрақты болып қалады: F1h1 = F2h2.

11.Ньютонның заңдары.

Ньютонның бірінші заңы (немесе инерция заңы) әр алуан жүйелердің санақ жүйелерінен инерциалдық жүйелердің класын бөліп шығарады.

Ілгерілемелі қозғалатын денелер өзінің жылдамдығының модулін және бағытын сақтайтын санақ жүйелері бар болады. Басқа денелердің әсері болмағанда өзінің жылдамдығын сақтайтын дененің қасиетін инерция деп атайды. Сондықтан Ньютонның бірінші заңы инерция заңы деп атайды. Алғаш инерция заңын Г.Галилей тұжырымдаған (1632 ж). Ньютон Галилейдің қорытындыларын жалпылап, оларды қозғалыс заңдарының қатарына қосты. Ньютон механикасында денелердің өзара әсерлесу заңдары инерциалдық санақ жүйелері үшін тұжырымдалады.

Инерциялық жүйелер шексіз көп. Барлық инерциялық жүйелер бір-біріне қатысты бірқалыпты және түзусызықты қозғалатын жүйелер класын құрайды. Қандай да бір дененің әр түрлі инерциялық жүйелердегі үдеулері бірдей. Инерциялық санақ жүйесіндегі жылдамдықтың өзгеру себебі – оның басқа денелермен әсерлесуімен байланысты.Басқа денелердің әсеріндегі дене қозғалысының сандық сипаттамасын беру үшін екі жаңа физикалық шаманы – дененің инертті массасын және күшті енгізу қажет.

Масса – дененің инерттілігін сипаттайтын қасиеті. Егер екі дене бір бірімен әсерлессе, онда екі дененің де жылдамдығы өзгереді, яғни өзара әсерлесу нәтижесінде екі дене де үдеу алады. Берілген екі дененің үдеулерінің қатынасы кез келген жағдайда тұрақты болады. Физикада әсерлескен денелердің массалары олардың үдеулеріне кері пропорционал болатыны қабылданған:

Формуланың оң жағындағы «минус» таңбасы әсерлескен денелердің үдеулері қарама-қарсы бағытталатынын көрсетеді. Кез келген дененің массасы тәжірибеде эталон массасымен салыстырумен анықталады ().m1 = mэт = 1 кг.

болсын. Онда

.

Дененің массасы – скаляр шама. Тәжірибе көрсеткендей, егер массалары m1 және m2 екі денені біріктірсе, онда құрама дененің массасы m m1 және m2 массаларының қосындысына тең.m = m1 + m2.

Массалардың мұндай қасиеті аддитивтілік деп аталады.

Күш – бұл денелердің өзара әсерлесуінің мөлшерлік өлшемі. Күш дене жылдамдығының өзгеруінің себебі болып табылады. Ньютон механикасында күштердің әр түрлі себебі болуы мүмкін: үйкеліс күші, ауырлық күші, серпімді күш, т.б. Күш – векторлық шама. Денеге әсер ететін барлық күштердің векторлық қосындысы тең әсерлі күш деп аталады. Күшті өлшеу үшін, күш эталонын және басқа денелерді осы эталонмен салыстыру тәсілін анықтау қажет. Күш эталоны ретінде белгілі ұзындыққа дейін созылған серіппені алуға болады.

1.7.3.-сурет. күшін эталонмен салыстыру. F = F0

Ньютонның екінші заңы – динамиканың негізгі заңы. Бұл заң тек инерциялық санақ жүйелерінде орындалады. Екінші заңды тұжырымдамас бұрын, динамикада екі жаңа физикалық шама – дененің массасы m және күш , сонымен бірге оларды өлшеу тәсілдері енгізілетін ұмытпау қажет. Осы шамалардың біріншісі – масса m – дененің инертті қасиеттерінің сандық сипаттамасы болып табылады. Ол дененің сыртқы әсерлеріне қалай жауап беретінін көрсетеді. Екіншісі - күш - бір дененің екінші денеге әсерінің сандық өлшемі.

Ньютонның екінші заңы – табиғаттың фундаментальды заңы, ол келесі екі категорияға жіктеуге болатын тәжірибелік деректердің жалпылауы болып табылады:

1. Егер массалары әр түрлі денелерге бірдей күшпен әсер етсе, онда денелер алатын үдеу массаларға кері пропорционал болады:

2. Егер бір денеге әр түрлі күшпен әсер етсе, онда дененің үдеуі салынған күштерге тура пропорционал болады:

Осы тәрізді бақылауларды жалпылай отырып, Ньютон динамиканың негізгі заңын тұжырымдады:

Денеге әсер ететін күш дене массасы мен оған берілген үдеудің көбейтіндісіне тең болады.

Ньютонның екінші заңы массасы және осы денеге әсер ететін күш белгілі болған жағдайда, үдеуді табуға мүмкіндік береді.

Халық аралық бірліктер жүйесінде массасы 1 кг денеге 1 м/с2 берілген үдеу әсер ететін күш алынады. Бұл бірлік ньютон деп аталады. Оны СИ-да күш эталоны ретінде қабылдайды.

Егер денеге бір уақытта бірнеше күш әсер етсе, мысалы және , онда тең әсерлі күш:

1.8.1.-сурет. күші – шаңғышыға әсер ететін ауырлық күшінің және нормаль

қысымының тең әсерлі күші. күші шаңғышының үдеуін тудырады.

Егер тең әсерлі күш 0-ге тең болса, онда дене тыныштық қалпын немесе бірқалыпты түзусызықты қозғалысын сақтайды. Сонымен, Ньютонның екінші заңы дербес жағдайда Ньютонның бірінші заңын қосады.

масса ұғымы екі әсерлескен дененің үдеулерін өлшеу негізінде анықталды: әсерлескен денелердің массалары үдеулердің сандық мәндеріне кері пропорционал:

Векторлық формада бұл қатынас

түрінде жазылады. «Минус» таңбасы әсерлескен денелердің үдеулері әрқашан қарама-қарсы бағытталатынын көрсетеді. Ньютонның екінші заңына сәйкес,

және

күштері денелердің үдеулерін тудырады. Осыдан:

шығады. Бұл теңдік Ньютонның үшінші заңы деп аталады.

Денелер бір-біріне модулі жағынан тең, ал бағыты жағынан қарама-қарсы күшпен әсер етеді. Бұл күштер әр түрлі денелерге салынған, сондықтан бір-бірін теңестіре алмайды.

1.9.1.-сурет. Ньютонның үшінші заңы.

. Бір денеге салынған күштерді ғана векторларды қосу ережесі бойынша қосуға болады. 1.9.1.-суреті Ньютонның үшінші заңын суреттейді. Адам жүкке модулі жағынан қандай күшпен әсер етсе, жүк те адамға сондай күшпен әсер етеді. Бұл денелер қарама-қарсы бағытта бағытталған. Олардың физикалық табиғаты бірдей – бұл жіптің серпімді күштері. Екі денеге берілген үдеулер денелер массаларына кері пропорционал.

Бір дененің бөліктерінің арасында әсер ететін күш ішкі күш деп аталады. Егер дене бүтін болып қозғалса, онда оның үдеуі сыртқы күшпен анықталады. Ішкі күштер Ньютонның екінші заңынан шығарылған, өйткені олардың векторлық қосындысы нөлге тең. Мысал ретінде 1.9.2. суретін қарастырайық, мұнда массалары m₁ және m₂ болатын екі дене салмақсыз созылмайтын жіппен және бірдей үдеуімен қозғалатын сыртқы күшінің әсерінен қозғалады. Денелердің арасында Ньютонның үшінші заңына бағынатын ішкі күштер әсер етеді:

Әрбір дененің қозғалысы олардың арасындағы әсерлесу күшіне байланысты. Әрбір денеге қолданылған Ньютонның екінші заңы:

береді. Осы теңдеулердің сол және оң жақтарын қосып және

,

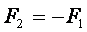
болатынын ескерсек:

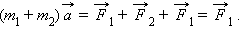
аламыз. Ішкі күштер екі байланысқан денелердің қозғалыс жүйесінің теңдеуінен алынып тасталды.

12.Материялық нүктенің импульс моменті. Күш моменті. Инерция моменті. Күш моменті M деп айналу осіне dқашықтығында нүктеге түсірілген F күштің көбейтіндісімен анықталатын шаманы айтамыз:M=Fd.

d айналу осінен әсер ететін күш нүктесіне дейінгі қашықтық (м). М күш моменті (н*м). Fәсер етуші күш (н). Айналмалы қозғалысты зерттеу үшін екі жаңа физикалық шама-күш моменті және инерция моменті қажет. Қос күштің моменті деп,шамасы бойынша бір-біріне тең,қарама-қарсы бағытталған, бір түзудің бойымен әсер етпейтін екі күшті айтады. Өн бойымен күштер әсер ететін түзулердің l –арақашықтығы қос күштің иіні деп аталады. Қос күштің кез келген нүктеге қатысты моменті біреу-ақ болады. Егер де О нүктесіне қатысты еркінше айналатын болса, онда дене fкүшінің әсерімен осьтен бұрылады, ал бұл ось күш пен О нүктесі жатқан жазықтыққа перпендикуляр,яғни ол берілген нүктеге қатысты күш моментінің бағытымен сәйкес келеді. Моменттің шамасы күштің денені осы осьтен айналдыра алатын күштің қабілеттігін сипаттайды. Егер дене тек кейбір белгіленген осьтен ғана айнала алатын болса,онда денені осы осьтен айналдыра алатын күштің қабілеттілігі оське қатысты моменті деп атайтын шамамен сипатталады. Материялық нүктенің импульс моменті күш моменті сияқты анықталады. О нүктесіне қатысты импульс моменті мынаған тең:L=[rp]=m[rv] мұндағы r-нүктесінен материялық нүкте орналасқан кеңістік нүктесіне жүргізілген радиус вектор. P=mv-нүкте импульсі. Материялық нүктелердің тұйық системасы үшін М=0 осының салдарынан L импульсінің қосынды моменті уақытқа тәуелді болмайды. Импульс моментінің сақталу заңы:материялық нүктелердің тұйық системасының импульс моменті тұрақты болып қалады. V ныВекторлық түрде жазсақ:P= . Екі дене абсолют серпімді соқтығысқанда, екі дене импульс және энергиямен алмасады. Соқтығысқаннан кейінбастапқы жылдамдықтарынан өзгеше жылдамдықтармен қозғалады, бағыттары да өзгеруі мүмкін. Бірақ энергия және импульс сақталу заңлары негізінде толық импульс және энергиялары өзгермейді.m1v1+m2v2= +m2v2. материялық нүкте z осіне қатыстыматериялық системасының инерция моменті деп аталады. Жеке алынған қосылғышы z осіне қатысты і-нші материялық нүктенің инерция моменті болып табылады. Инерция моментін мына түрде көрсетуге болады:I= . Бұл жерде элеме

Date: 2016-07-22; view: 8226; Нарушение авторских прав