Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?
Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника
Наведение ЭДС в обмотках электрических машин
|
|
Электродвижущая сила в витке может наводиться при вращении витка в магнитном поле или при перемещении магнитного поля относительно витка (рисунок 1.78, а). Электродвижущая сила в витке наводится также, если неподвижный виток пронизывается изменяющимся во времени магнитным потоком (рисунок 1.78, б). В общем случае ЭДС в витке наводится при пространственном перемещении поля и витка относительно друг друга, а также при изменении потока, сцепленного с витком, во времени.
Электродвижущая сила, обусловленная относительным перемещением витка и поля, называется ЭДС вращения. Электродвижущую силу, зависящую от изменения потока во времени, называют трансформаторной ЭДС.
Рисунок 1.78, Наведение ЭДС в витке
Электродвижущую силу вращения можно определить по формуле, предложенной Фарадеем (рисунок 1.78, а):
ex = Bx × ld × u,
(1.59)
где ld — активная длина витка; u — линейная скорость.
Электродвижущая сила секции (катушки), состоящей из нескольких витков,
e = - w
d Ф= - d Yk,
(1.60)
k k × dt dt
где потокосцепление
|
× cos(wt - a),
(1.61)
|
Y — максимальное потокосцепление катушки (рисунок 1.79). На комплексной
|
Рисунок 1.79. ЭДС и потокосцепления на комплексной плоскости
Электродвижущая сила катушки
e = - d Yk
= - d Ykm × cos(wt - ak) = w × Y
cos(wt - a).
(1.62)
k dt dt
km k
Действующее значение ЭДС катушки
|
(1.62)
На комплексной плоскости из (1.62)
|
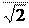Ek = - j km
(1.63)
Электродвижущая сила, которая наводится в катушке, зависит от выполнения катушки. В катушке, состоящей из витков с диаметральным шагом (рисунок 1.80, а), максимальный поток от 1-й гармоники индукции равен
Ф = B
× l × t
= 2 × B
S,
(1.64)
m ñð d
p 1 m
где
B 1 m— амплитуда индукции первой гармоники;
S = ld × t — площадь,
пронизываемая потоком. Тогда ЭДС проводника eпр = Eпрm × sin(wt),
где амплитуда ЭДС
(1.65)
Eпрm= Bx × ld
× u = 2 × f
Bx × ld
× t.
(1.66)
Так как
× u = 2 × f
то
× t,
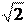(1.67)
E
Eпр= =
f × Bx
× ld
× t.
(1.68)
Рисунок 1.80. К определению ЭДС в катушке с диаметральным (а) и укороченным (б) шагами
Для катушки с витками, имеющими укорочение (рисунок 1.80, б)
Ф = k у× Ф,
(1.69)
где ky — коэффициент укорочения, который учитывает уменьшение ЭДС засчет укорочения шага витков катушки.
При укорочении шага относительный шаг
b = y t
(1.70)
меньше единицы. При этом ЭДС двухпроводников витка
пр и
E¢¢ одинаковые, но
|
|
æ bp ö
Eв= 2 × Eпр× sinç ÷.
è 2 ø
(1.71)
Коэффициент укорочения равен отношению геометрической суммы ЭДСк арифметической сумме:
æ bp ö
ky = ×sinç ÷.
è 2 ø
(1.72)
Рис. 1.71. ЭДС внткаEвобмоткн с укороченным шагом
При шаге витка
y» 0,8 кy 0,95 - 0,98. Можно выполнить катушку с удлиненным
шагом, когда меди. Однако
y > 1. При этом увеличивается длина лобовых частей и растет расход
кy также меньше единицы, так как результирующий поток уменьшается
(рисунок 1.82, а). При
y = 2 × t результирующий поток, пронизывающий контур
катушки, равен нулю (рисунок 1.82, б).
Рисунок 1.82. К определению коэффициента укорочения в катушке с удлиненным шагом
Поле в воздушном зазоре электрических машин отличается от синусоиды. Высшие гармоники появляются за счет несинусоидального распределения МДС, наличия зубцов на статоре и роторе (рисунок 1.83), насыщения и других причин.
Для уменьшения влияния высших гармоник на характеристики машины применяют обмотки с укороченным шагом, выполняют скос пазов и принимают другие меры. Скос пазов выполняется на зубцовое деление статора и ротора и обеспечивает уменьшение влияния высших гармоник, так как в скошенном витке ЭДС от высших
гармоник компенсируется (рисунок 1.84): ЭДС направлены встречно.
e 5¢ в одной части витка и e 5¢¢ в другой
Рисунок 1.83. Искажение поля в воздушном зазоре
Рисунок 1.84. Компенсация ЭДС высших гармоник в витках, лежащих в скошенных пазах
При скосе пазов уменьшается ЭДС и 1-й гармоники. Уменьшение ЭДС 1-й гармоники
за счет скоса определяет коэффициент скоса
kск. При скосе пазы статора и ротора
|
(рисунок 1.85):
|
(1.73)
где v — номер гармоники;
bск
— скос, показывающий, насколько сдвинута ось
|
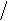
kск
= [sin(g
2)] 0,5 × g
ск.
(1.74)
Рис. 1. 75. К определению пазы статора;
пазы ротора
kск :
При скосе, равном зубцовому делению, получаем
kск для1-йгармоникиблизкимк
единице. Для высших гармоник
kск существенноменьшеединицы.
Скос пазов уменьшает влияние высших гармоник на работу машины, улучшая форму ЭДС и снижая шумы и вибрации. Однако скос пазов увеличивает длину витка, что приводит к увеличению активного сопротивления и индуктивного сопротивления рассеяния.
Такимобразом,ЭДСкатушкис учетом коэффициентов k у
следующим образом:
и kск
можно определить
Ek= wk ×× Eв= 2 × wk ×× Eпр= 2 ×
f × wk ×× k у× kск × B 1 m × ld × t.
(1.75)
Поток на полюсном делении
Ф = B
× l × t = 2 × B
× l × t,
(1.76)
ср d
p 1 m d
тогда ЭДС катушки
|
× f × wk × × k у× kск × Ф = 4,44 × f
wk × × k у× kск × Ф.
(1.77)
Обычно обмотки электрических машин состоят из катушечных групп. Каждая катушечная группа состоит из q катушек, соединенных последовательно и лежащих в соседних пазах.
Электродвижущаясилакатушечнойгруппы Еq равнагеометрическойсуммеЭДСотдельных катушек, а не их арифметической сумме из-за того, что катушки расположены в пазах на внутренней или внешней поверхности цилиндра статора или ротора, сдвинутых относительно друг друга в магнитном поле 1-й гармоники на угол
a = p
m × q.
Коэффициент распределения обмотки характеризует уменьшение ЭДС из-за пространственного сдвига катушек по отношению друг к другу и равен (рисунок 1.86)
k p = Eq
q × Ek.
(1.78)
Из рисунка 1.86 следует, что
|
|
2).
2)= 2 × R × sin(a
(2 × q)).
Рисунок1.86.К определению коэффициентараспределения k p
Тогда коэффициент распределения m-фазной обмотки определится выражением
|
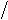
2)] q × sin(a (2 × q)).
(1.79)
|
k p= 1. При
q > 1 k < 1.
|
АВ:
q ® ¥, k естьотношениехорды АВ к длине дуги
k = [sin(a
2)] (a
2).
p¥ (1.80)
Значение
k p¥
при заданном угле a является наименьшим значением
k p. При
распространенных в практике электромашиностроения числах пазов на полюс и фазу (
|
Электродвижущая сила катушечной группы для 1-й гармоники
Eq = p
q × f
wk ×× k об× Ф.
(1.81)
где
k об— обмоточный коэффициент;
k об= k у× kр × kск.
(1.82)
Обмоточный коэффициент, как правило, меньше единицы:
k об» 0,9 - 0,98.
Коэффициент
k обхарактеризует уменьшение ЭДС в реальной машине за счет
укорочения шага обмотки, выполнения ее в пазах на статоре или роторе и наличия скоса пазов.
Произведение
k об w
называют эффективным числом витков, так как поток полюса во
вращающихся электрических машинах в отличие от трансформаторов сцепляется с катушкой не полностью.
Для определения ЭДС фазы обмотки можно воспользоваться выражением (1.81), в котором вместо числа витков в катушечной группе qw подставляется число
последовательно соединенных витков фазы последовательно соединенных катушечных групп:
w = n × q × wk, где п — число
Eф = p
× f × w × k об× Фm = 4,44 × f
w × k об× Фm.
(1.83)
В обмотках машин переменного тока катушечные группы, лежащие под разными полюсами, содержат одинаковое число катушек и занимают одинаковые дуги на внутренней окружности статора или ротора (или число пазов), поэтому катушечные группы симметричны и в них наводятся одинаковые ЭДС. Эти группы можно соединить последовательно или параллельно.
Число витков фазы обмотки для т- фазной обмотки с числом а параллельных ветвей определяется по формуле
w = z × S п
(2 × a × m),
(1.84)
гдеSп—числоэффективныхпроводниковв пазу. Эффективный проводник может состоять из одного или нескольких соединенных параллельно витков.
Для определения ЭДС фазы обмотки используется также векторная диаграмма ЭДС катушечной группы, которую называют звездой пазовых ЭДС (рисунок 1.87). Звезда пазовых ЭДС на рисунке 1.87 дана для трехфазной обмотки т= 3, р= 1, q=3 (см. рисунок 1.64).
Рисунок. 1.87. Звезда пазовых ЭДС для трехфазной обмотки (р=1, q=3)
Электродвижущая сила фазы является векторной суммой ЭДС каждой катушки (рисунок 1.87). Звезда пазовых ЭДС (рисунок 1.87, а) дает возможность определить коэффициент распределения и ЭДС фазы (рисунок 1.87, б) для симметричных и несимметричных, двухфазных и многофазных обмоток, когда расчет по (1.83) встречает затруднения. Полученные выше выражения для 1-й гармоники можно распространить на высшие гармоники.
Электродвижущая сила фазы от высшей гармоники поля
Eф u = p
fu × w × k об u × Фmu.
(1.85)
где Фmu,
fu и
k об u — поток, частота и обмоточный коэффициент u -йгармоники.
Таккакполюсноеделение u -йгармоники tu
гармоники, то магнитный поток u -гармоники
в u раз меньше полюсного деления 1-й
Ф = 2 × B
× l × t =
2 × B
× l × t,
(1.86)
u p um d
u p × u
um d
где
Bum — амплитуда u -йгармоники индукции в воздушном зазоре машины. Для
временных гармоник
fu = u × f а для пространственных гармоник
fu = f 1.
Обмоточный коэффициент для v-й гармоники
k об u
= k у u × k рu × kскu.
(1.87)
где
k у u,
kрu, kскu
— соответственно коэффициенты укорочения, распределения и скоса
для u -й гармоники.
Относительно u -й гармоники угол сдвига проводников катушки равен upb (см. рисунок 1.83) и
æ ubp ö
k у u
= sinç ÷.
è 2 ø
(1.88)
Коэффициент распределения для v-й гармоники
k = [sin(up
2 m)] q × sin(up
(2 × q × m)).
рu (1.89)
Угол скоса паза относительно поля u -й гармоники (см. рисунок 1.84) в u раз больше, чем для 1-й гармоники, и коэффициент скоса для u -й гармоники
kскu
= [sin(u × b × p
2 t)] (u × b × p
2 t).
(1.90)
|
|
u, а f = f.
+ E 3
+ E 5
+...+ E 2.
(1.91)
|
Высшие гармоники искажают ЭДС, и форма напряжения становится несинусоидальной. Несинусоидальность напряжения в сетях и приемниках электрической энергии вызывает дополнительные потери, приводит к ухудшению КПД и cosφ. Высшие гармоники являются также причиной шумов и вибраций в электрических машинах.
Чтобы снизить ЭДС от высших гармоник, стремятся подавить высшие гармоники за счет укорочения шага обмотки, распределения обмотки по пазам (выбора достаточно большого q) и скоса пазов.
На форму ЭДС оказывает также влияние выбор схемы соединения обмоток.
В многофазных системах применяются в основном два соединения — в многофазную звезду и в многоугольник. В трехфазной системе, применяющейся в энергетике, во вращающихся машинах используются соединения в звезду и треугольник (рисунок 1.88).
Рисунок 1.88. Соединение обмоток в звезду (а) и треугольник (б)
В трехфазных системах особое положение имеют 3-я гармоника и кратные ей нечетные гармоники (u =9, 15, 21 и т. д.). В пятифазных системах особое место занимают 5-я гармоника и кратные ей гармоники и т. д.
В трехфазной системе в фазах А, В, С 1-е гармоники сдвинуты на 120° относительно друг друга. Электродвижущие силы гармоник, кратных трем, в фазах А, В и С
совпадают по фазе и при соединении в звезду в линейных напряжениях эти гармоники отсутствуют (рисунок 1.88). При соединении обмоток в треугольник ЭДС гармоник, кратных трем, складываются и создают ток, циркулирующий внутри обмоток. Эти особенности необходимо учитывать при проектировании электрических машин и трансформаторов.
Как правило, высшие гармоники ухудшают характеристики и энергетические показатели электрических машин. Высших гармоник поля нет только в идеальной электрической машине, в зазоре которой имеется круговое поле. При проектировании электрических машин стремятся поле в машине максимально приблизить к синусоидальному.
2) УРАВНЕНИЯ ТРАНСФОРМАТОРА
|
и между подвижными обмотками статора и ротора, сдвинутыми на электрический угол, равный 90°, магнитные связи отсутствуют.
Рассмотрим вначале уравнения ненасыщенного однофазного двухобмоточного
трансформатора, у которого число витков первичной обмотки
w 1 равночислувитков
вторичной обмотки
w 2. На рисунке 2.3 дана схема однофазного трансформатора, на
которой для удобства изображения первичная и вторичная обмотки расположены на разных стержнях. В реальных трансформаторах для обеспечения лучшей магнитной связи обмотки располагаются на одном стержне.
Рисунок 2.3. Схема однофазного трансформатора
Date: 2016-07-22; view: 1261; Нарушение авторских прав