Векторная диаграмма асинхронной машины

У асинхронных машин число витков на роторе и статоре различное. Процессы преобразования энергии принципиально не изменятся, если рассматривать машину с одинаковыми числами витков на роторе и статоре. Обычно число витков обмотки ротора приводится к числу витков обмотки статора. При приведении сохраняются потребляемая из сети активная и реактивная мощности, КПД и cosφ. В обозначения приведенных величин добавляют штрих.

Сохраняя неизменными МДС приведенной обмотки и реальной, как и для трансформаторов, получим приведенный ток вторичной обмотки

I ¢ = I

m 2× w 2× k об2,

(3.16)

об1

где

m 1,

m 2 —числафаз обмоток статора и ротора;

w 1,

w 2 — числа витков фазы

статора и ротора;

k об1,

k об2— обмоточные коэффициенты обмоток статора и ротора.

Из условия неизменности потока в машине с приведенным числом витков обмотки и с действительным числом витков

= E 2¢

4,44 × w 1× k об1× f 1

(3.17)

получим

E ¢= E ¢

w 1 × k об1.

(3.18)

об2

× r 2 = m 1 × (I 2¢)

× r 2¢,

(3.19)

найдем

æ × × ö

r ¢ = I 2

m 2× r

m

w 1 k об1

÷

m 2× r

= m 1 çç w 1

k об1 ÷÷ r.

(3.20)

è m 2

w 2

k об2 ø m 1

m 2 è w 2

k об2 ø

Из условия неизменности реактивной мощности имеем

m 2× r

m æ w

= 1 çç 1

(3.21)

m 2 è w 2

k об2 ø

Таким образом, коэффициент приведения для тока

m 1× w 1× k об1

I ¢ = k

(3.22)

Коэффициент приведения ЭДС и напряжения

U ¢ = k

× U.

(3.23)

w 1 × k об1

2 U 2

Коэффициент приведения сопротивлений

об1

÷

(3.24)

kI m 2 è w 2 × k об2 ø

При этом

z 2¢ = z 2 × kz.

(3.25)

При приведении короткозамкнутой обмотки ротора считают, что число стержней

z 2= m 2, а число витков

w 2 = 1 2, что следует из определения числа зубцов, когда

р =1 и q =1. Тогда для короткозамкнутого ротора

(w × k

(3.26)

Уравнения приведенной асинхронной машины согласно (3.15) выглядят следующим образом:

U 1= - E 1+ z 1× I 1; ü

ï

0 = E ¢ -

j × x ¢× I ¢ - I ¢ r 2¢;ï

(3.27)

ï

I 0 = I 1 + I 2¢. ïþ

Геометрическим изображением (3.27) на комплексной плоскости является векторная диаграмма асинхронной машины (рисунок 3.16).

Векторная диаграмма асинхронной машины отличается от векторной диаграммы

трансформатора тем, что

U 2¢ = 0, а ЭДС ротора

E 2¢ определяется падением

напряжения на индуктивном сопротивлении ротора

I ¢ r 2¢ = I ¢ × r ¢ + I ¢ × r ¢ 1 - s,

j × x 2¢

и активном сопротивлении:

(3.28)

2 s 2 2

2 2 s

где

I 2¢ × r 2¢

— падение напряжения на активном сопротивлении обмотки ротора;

I ¢ × r ¢1 - s

— напряжение, характеризующее механическую мощность на валу

2 2 s

машины Р 2.

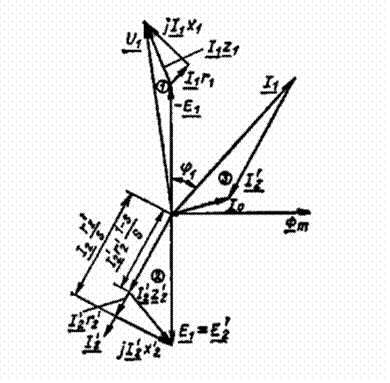
Рисунок 3.15. Векторная диаграмма асинхронной машины Действительно, если умножить члены равенства (3.28) на

I 2¢ и

m 1, то получим

m × (I ¢)2× r ¢+ m

× (I ¢)2× r ¢1 - s,

1 2 2

1 2 2 s

где первый член определяет потери в роторе, а второй

m × (I ¢)2× r ¢1 - s = m

× (I

)2× r

1 - s = m

× U ¢ × I ¢.

(3.29)

1 2 2 s

2 2 2 s

1 2 2

определяет механическую мощность на валу машины

P 2¢. Мощность

P 2¢включаетв

себяполезнуюмощностьнавалумашины Р 2 и механические потери Р мех.

Для разделения механических потерь и полезной мощности на валу машины можно

1 - s

ввести эквивалентные активные сопротивления, выделив их из

r ¢. В

асинхронных двигателях единых серий скольжение изменяется в небольших пределах (sном=1-4%),поэтомумеханическиепотериможносчитатьпостоянными.

Векторная диаграмма на рисунке 3.16 построена для одной фазы машины. Поэтому

для определения

P 2¢в (3.29) необходимо произведения токов и напряжений умножить

на число фаз статора или ротора.

На векторной диаграмме уравнениям статора соответствуют треугольник 1, уравнениям ротора — треугольник 2 и уравнениям токов — треугольник 3.

В асинхронных машинах, как и в трансформаторах, намагничивающий ток

I 0 = I 1 + I 2¢. При этом результирующая МДС из (3.27)

F 0=

m 1×

P

w 1 × k об1 p

I 1 +

m 1×

P

w 2 × k об2 p

I 2¢.

(3.30)

Результирующая МДС и МДС обмоток ротора и статора — пространственные векторы, так как МДС обмоток создаются благодаря определенному пространственному сдвигу обмоток и временному сдвигу токов. При построении

векторной диаграммы можно использовать намагничивающий фазный ток результирующую МДС обмотки.

I 0 или

При построении векторной диаграммы совмещаются временные U, I, E и

пространственные

F, F векторы. При анализе рабочих процессов в асинхронных

машинах целесообразно пользоваться результирующими векторами U, I, F, Y и

m, сочетающими временные и пространственные представления.

Построение диаграммы начинается с того, что в масштабе откладывают вектор потока

I 0 не совпадет с

F, так как намагничивающий ток

I 0 = I 0 a +

jI 0 p.

(3.31)

После определения тока

I 0 по магнитному потоку m

рассчитывают ЭДС

E 1 = E 2¢ и

I 2. По (3.22) ток ротора приводят к обмотке статора и по (3.27)

находят ток статора

I 1. Затем по известным ЭДС, токам и сопротивлениям по (3.27)

строят векторную диаграмму.

Векторные диаграммы можно построить для нескольких значений токов нагрузки, и по ним можно судить об изменении токов, потерь, cosφ и падений напряжений при изменении нагрузки на валу машины.

При холостом ходе асинхронного двигателя

P 2 = 0

и ток холостого хода

I 0= I 1

так

как можно считать, что

I 2¢» 0. Ток в роторе равен нулю, если механические потери

равны нулю. При холостом ходе активная мощность, потребляемая из сети, небольшая

и ток

I 1 имеет в основном реактивную составляющую. При этом реактивная

мощность, необходимая для создания магнитного поля, поступает из сети и ток I 1

отстает от

U 1. Коэффициент мощности cosφ характеризует соотношение между

активной и реактивной мощностями.

С ростом нагрузки растет ток в роторе

I 2¢, увеличивается и ток в статоре

I 1. Из-за

падения напряжения на обмотке статора несколько уменьшается

E 1, что приводит к

и снижению

I 0. Однако в первом приближении

можно принять, что

I 0 при изменении нагрузки не изменяется. Это облегчает

построение векторных диаграмм. С увеличением нагрузки на валу увеличивается скольжение, растут электрические потери в роторе и статоре, растет потребляемая из

сети активная мощность

неизменной.

P 1, а реактивная мощность практически остается

На рисунках 3.16, а—в представлены векторные диаграммы асинхронной машины в двигательном режиме, при холостом ходе и в генераторном режиме.

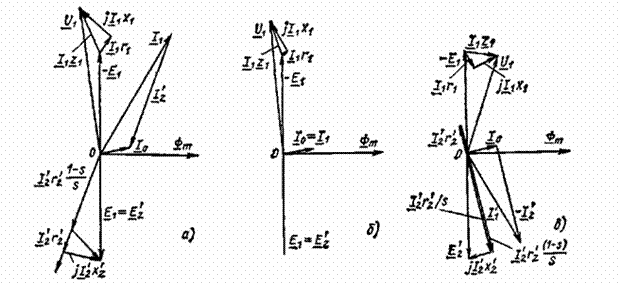
Рисунок 3.16. Векторные диаграммы асинхронной машины в режиме двигателя (а), холостого хода (б) и генератора (в)

Векторные диаграммы асинхронных машин при проектировании практически не используются, но они имеют важное методическое значение при изучении асинхронных машин.

Билет 10

Date: 2016-07-22; view: 608; Нарушение авторских прав