Полное приращение и полный дифференциал.

Определение Для функции f(x, y) выражение Dz = f(x + Dx, y + Dy) – f(x, y) называется полным приращением.

Если функция f(x, y) имеет непрерывные частные производные, то

Тогда получаем, применив теорему Лагранжа

Т.к. частные производные непрерывны, то можно записать равенства:

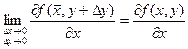
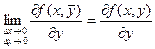
Определение. Выражение называется полным приращением функции f(x, y) в некоторой точке (х, у), где a₁ и a₂ – бесконечно малые функции при Dх ® 0 и Dу ® 0 соответственно.

Определение: Полным дифференциалом функции z = f(x, y) называется главная линейная относительно Dх и Dу приращения функции Dz в точке (х, у).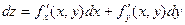

Для функции произвольного числа переменных:

Пример. Найти полный дифференциал функции .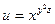

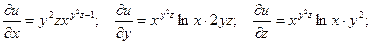
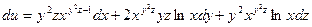
Пример. Найти полный дифференциал функции

Геометрический смысл полного дифференциала.

Касательная плоскость и нормаль к поверхности.

нормаль

N

j N₀

касательная плоскость

Пусть N и N₀ – точки данной поверхности. Проведем прямую NN₀. Плоскость, которая проходит через точку N₀, называется касательной плоскостью к поверхности, если угол между секущей NN₀ и этой плоскостью стремится к нулю, когда стремится к нулю расстояние NN₀.

Определение. Нормалью к поверхности в точке N₀ называется прямая, проходящая через точку N₀ перпендикулярно касательной плоскости к этой поверхности.

В какой – либо точке поверхность имеет, либо только одну касательную плоскость, либо не имеет ее вовсе.

Если поверхность задана уравнением z = f(x, y), где f(x, y) – функция, дифференцируемая в точке М₀(х₀, у₀), касательная плоскость в точке N₀(x₀,y_0,(x₀,y₀)) существует и имеет уравнение:

.

Уравнение нормали к поверхности в этой точке:

Геометрическим смыслом полного дифференциала функции двух переменных f(x, y) в точке (х₀, у₀) является приращение аппликаты (координаты z) касательной плоскости к поверхности при переходе от точки (х₀, у₀) к точке (х₀+Dх, у₀+Dу).

Как видно, геометрический смысл полного дифференциала функции двух переменных является пространственным аналогом геометрического смысла дифференциала функции одной переменной.

Пример Найти уравнения касательной плоскости и нормали к поверхности

в точке М(1, 1, 1).

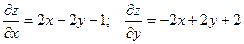
Уравнение касательной плоскости:

Уравнение нормали:

Частные производные высших порядков.

Пусть имеется некоторое множество Х в пространстве . Каждая точка этого множества определяется набором чисел , которые являются координатами данной точки. Будем говорить, что на множестве Х задана функция n-переменных, если каждой точке 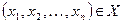по определенному закону ставится в соответствие единственное число z, т.е. .

Пример: пусть х₁, х₂, х₃ – длина, ширина и глубина бассейна. Тогда найдем площадь поверхности бассейна.

.

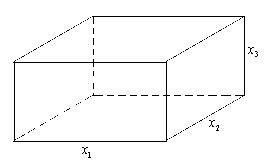
Функция n-переменных называется непрерывной в точке 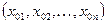, если предел функции в этой точке равен значению функции в предельной точке, т.е. .

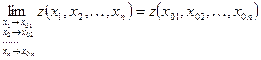Определение: частной производной функции по переменной называют производную от функции z по переменной , вычисленную при условии, что все остальные переменные остаются постоянными.

частная производная.

Пример

Для функции двух переменных можно ввести четыре частные производные второго порядка , тогда

1. 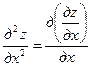, читается: два z по дважды.

2.

3.

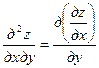
4.

Теорема смешанные производные, там где они непрерывны, не зависят от порядка вычисления производных. Это справедливо для смешанных производных любого порядка и для функции от любого количества переменных.

Если функция f(x, y) определена в некоторой области D, то ее частные производные 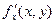и 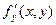тоже будут определены в той же области или ее части.

Будем называть эти производные частными производными первого порядка.

Производные этих функций будут частными производными второго порядка.

Продолжая дифференцировать полученные равенства, получим частные производные более высоких порядков.

Определение Частные производные вида и т.д. называются смешанными производными.

Теорема Если функция f(x, y) и ее частные производные определены и непрерывны в точке М(х, у) и ее окрестности, то верно соотношение: .

Т.е. частные производные высших порядков не зависят от порядка дифференцирования.

Аналогично определяются дифференциалы высших порядков.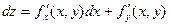

…………………

Здесь n – символическая степень производной, на которую заменяется реальная степень после возведения в нее стоящего в скобках выражения.

Экстремум функции нескольких переменных.

Определение Если для функции z = f(x, y), определенной в некоторой области, в некоторой окрестности точки М₀(х₀, у₀) верно неравенство то точка М₀ называется точкой максимума.

Определение Если для функции z = f(x, y), определенной в некоторой области, в некоторой окрестности точки М₀(х₀, у₀) верно неравенство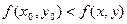

то точка М₀ называется точкой минимума.

Теорема (Необходимые условия экстремума) Если функция f(x,y) в точке (х₀, у₀) имеет экстремум, то в этой точке либо обе ее частные производные первого порядка равны нулю , либо хотя бы одна из них не существует.

Эту точку (х₀, у₀) будем называть критической точкой.

Теорема (Достаточные условия экстремума) Пусть в окрестности критической точки (х₀, у₀) функция f(x, y) имеет непрерывные частные производные до второго порядка включительно. Рассмотрим выражение:

1) Если D(x₀, y₀) > 0, то в точке (х₀, у₀) функция f(x, y) имеет экстремум, если

2) - 0, то в точке (х₀, у₀) функция f(x, y) не имеет экстремума

В случае, если D = 0, вывод о наличии экстремума сделать нельзя.

Date: 2016-07-18; view: 589; Нарушение авторских прав