Элементы теории погрешностей

Получаемые расчетными методами результаты обычно содержат погрешности. Это вызывается рядом объективных причин. В данном случае нас интересуют те причины, которые будут связаны с методами вычислений. Такие погрешности называются вычислительными. Познакомимся с основными типами погрешностей и правилами работы с ними.

Пусть А -точное значение некоторой величины, - известное приближение к нему, т.е. приближенное значение величины А. Обозначим или 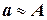. Число А принято называть точным числом, а его приближение - приближенным числом. Например, в соотношениях

число - является точным; числа 3,14; 3,142 – приближенные.

Разность или () между точным и приближенным значениями величины называется погрешностью значения 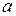(но не А). Так как эта разность может иметь разный знак, а степень точности приближения не зависит от знака и ее удобно характеризовать с помощью неотрицательных чисел, вводится понятие абсолютной погрешности:

.

Знак () свидетельствует о том, что погрешность между А и 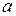не больше (но может быть и меньше). Действительно, совершенно неважно или . Главное - насколько они отличаются.

Абсолютная погрешность дает ценную информацию о неизвестном точном значении А: оно находится от известного приближения () на расстоянии, не большем, чем . Можно записать:

.

Следовательно, найдя приближенное значение 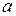и его абсолютную погрешность , узнаем, что точное значение А располагается на отрезке , но где точно - ответить на этот вопрос нельзя. Отклонение

;

называется относительной погрешностью. Она позволяет оценить точность несопоставимых чисел. Часто используют соотношения:

.

Если известна абсолютная погрешность приближенного значения а, то а называется приближением к А с точностью до . Когда говорят, что надо получить результат с заданной точностью ε, это означает, что его абсолютная погрешность не должна быть больше ε.

Все цифры дробной части (десятичной) записи числа, начиная с первой ненулевой цифры слева, называются значащими цифрами этого числа. Нули в конце числа всегда считаются значащими, в противном случае их не пишут. Например, числа 0,5020 и 0,05020 имеют одинаковые значащие цифры: 5; 0; 2; 0. Абсолютную погрешность не следует записывать с большим количеством значащих цифр. Основной информацией, содержащейся в ней, является значение первой ненулевой цифры и десятичный разряд, в котором эта цифра расположена (например, ± 0,004, ±0,0001).

В практике вычислений, производимых с приближенными числами, неизбежно возникает вопрос о влиянии погрешностей исходных чисел на погрешность конечного результата. Рассмотрим эту проблему подробнее.

Предположим, что вычисляется сумма С приближенных чисел А_i, т.е.

,

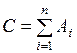где .

Искомую сумму можно записать так:

,

или ,

где , .

Итак, при сложении (вычитании) приближенных чисел результат является также приближенным числом, у которого абсолютная погрешность равна сумме абсолютных погрешностей всех слагаемых.

Относительная погрешность суммы рассчитывается следующим образом:

.

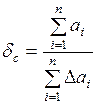Следует обратить внимание на то, что погрешность каждого слагаемого имеет знак (±), тем не менее при вычислении суммы (или разности приближенных чисел) погрешности слагаемых всегда записываются со знаком (+), но погрешность суммы ∆с будет иметь знак (±).

Правило расчета погрешности произведения (деления) приближенных чисел следующее. Если ищется результат произведения, например, двух приближенных чисел

,

где , ,

то первоначально можно получить значение только относительной погрешности произведения

,

и только вторично - значение абсолютной погрешности произведения

.

Эти выводы можно распространить на любое количество сомножителей. Действительно, если находится произведение приближенных чисел

,

где , , ,

то ,

где , .

При умножении приближенных чисел результат будет иметь относительную погрешность, равную сумме относительных погрешностей сомножителей, а абсолютная погрешность произведения должна вычисляться через относительную по общему правилу.

Из последнего правила можно, как частный случай произведения, получить зависимости для расчета погрешности при возведении приближенного числа в степень (равно как и вычислении корня из приближенного числа). Действительно, если вычисляется

,

где , ,

тогда .

Учитывая, что , а ,

запишем

,

,

.

Date: 2016-07-18; view: 381; Нарушение авторских прав