Вычисление квадратного корня из числа

Как известно, во всех языках имеется оператор SQRT(a), обозначающий процедуру вычисления корня квадратного из числа «а»:

.

Следует заметить, что все специальные математические операции являются циклическими, т.е. многократно повторяющимися по одному правилу. В математике существует понятие рекуррентной формулы типа:

,

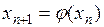когда новое значение переменной можно найти по предыдущему ее значению. Можно достаточно легко составить блок-схему алгоритма использования рекуррентной формулы (рисунок 2.5).

Рисунок 2.5 – Блок-схема алгоритма рекуррентной формулы

Вычисления по рекуррентной формуле называют итерацией. Основной характеристикой этих вычислений является скорость приближения к конечному результату (т.е. количеством расчетных циклов). Применительно к поставленной задаче можно записать несколько рекуррентных формул:

1) 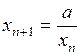; 2) ; 3) .

Эти формулы далеко не равнозначны. Если использовать первую формулу, то расчеты будут выполняться бесконечно долго и произойдет переполнение машины (т.е. процесс итерации будет расходиться). Вторая формула даст сходимость процесса только в ограниченном интервале существования переменной, а именно если (-1 < x < 0). Универсальность и высокую скорость сходимости обеспечивает только третья рекуррентная формула.

П р и м е р. Вычислить .

Выполним эту процедуру в десятеричной системе счисления поэтапно.

1) Положим 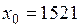. Тогда

.

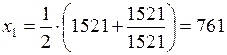2) Принимаем 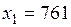. Тогда

.

………………………………………………………………………

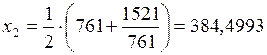8) Принимаем 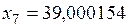. Тогда

.

На восьмом итерационном ходе получили точное значение корня из 1521.

П р и м е р. Вычислить .

Так как наиболее близкое значение к 1522 является число 1600, то для ускорения процесса счета назначим стартовое значение переменной и начнем итерационный процесс.

1) Положим . Тогда

.

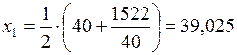2) Принимаем .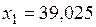

.

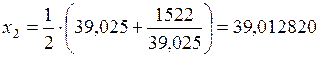3) Принимаем 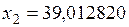. Тогда

.

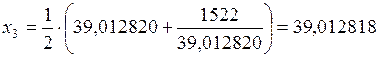Видим, что уже на третьей итерации получили шесть верных цифр. Однако можно просчитать, каким образом это число будет представлено в двоичной системе счисления. Проведем нормализацию числа 39,012818:

- целая часть числа ;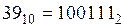

- дробная часть числа ;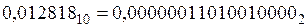

- нормализованное число

.

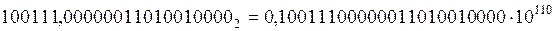Формат этого числа с учетом сдвига и первого разряда мантиссы представлен на рисунке 2.6.

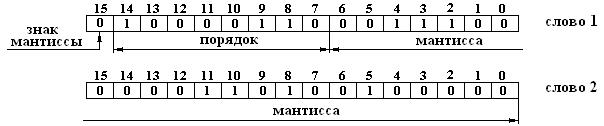
Рисунок 2.6 – Формат числа 39,012818

Однако применение двоичной системы счисления даст погрешность. Она находится при обратном переводе десятичной части числа:

.

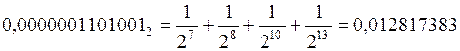Окончательно, значение 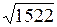в десятеричной системе счисления будет:

39,012818 - точное, 39,012817383 - рассчитанное машиной.

Видим, что уже в шестом знаке после запятой имеется погрешность .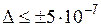

Date: 2016-07-18; view: 712; Нарушение авторских прав