Перевод чисел из одной системы счисления в другую

Рассмотрим процесс перевода в десятеричную систему числа А, записанного, например, в двоичной системе счисления (над каждой единицей укажем ее порядок):

Видим, что перевод с двоичной системы в десятеричную происходит решением многочлена. Такая технология перевода называется правилом замещения и выполняется без особых проблем.

Значительно сложнее алгоритм перевода числа из десятеричной системы счисления в двоичную. В этом случае для перевода любого числа используют правило деления – для перевода целой части числа и правило умножения – для перевода его дробной части. Чтобы перевести целое число А₁₀ из десятеричной системы в двоичную необходимо это число разделить на число 2 с остатком («нацело»). Затем неполное частное нужно снова разделить с остатком на 2 и т.д., пока последнее полученное неполное частное не станет равным нулю. Представлением числа А₂ в новой системе счисления будет последовательность остатков деления (это будут единицы и нули), записанных в порядке, обратном порядку их получения.

П р и м е р. Перевести число А₁₀=123 в двоичную систему с использованием десятеричной арифметики.

Р е ш е н и е. 123: 2 = 61 (1);

61: 2 = 30 (1);

30: 2 = 15 (0);

15: 2 = 7 (1);

7: 2 = 3 (1);

3: 2 = 1 (1);

1: 2 = 0 (1).

Тогда число А₂=1111011. Здесь числа 61, 30, 15 и т.д. – это неполные частные, а в скобках приведены остатки. Именно они, записанные снизу вверх, и сформировали число в новой системе счисления. Для подтверждения правильности перевода сделаем проверку.

.

Аналогично проводится процедура перевода целого числа, например, в восьмеричную или шестнадцатеричную системы.

П р и м е р. Перевести число А₁₀=123 в восьмеричную систему с использованием десятеричной арифметики.

Р е ш е н и е. 123: 8 = 15 (3)

15: 8 = 1 (7)

1: 8 = 0 (1).

Тогда число А₈=173. Проверка дает следующий результат:

.

П р и м е р. Перевести число А₁₀=123 в шестнадцатеричную систему с использованием десятеричной арифметики.

Р е ш е н и е. 123: 16 = 7 (11)

7: 16 = 0 (7).

Тогда число А₁₆=7В. Проверка дает результат:

.

Подведем итоги. Одно и то же число А₁₀=123 в десятеричной системе счисления принимает разный вид в рассмотренных выше системах:

А₂=1111011;

А₈=173;

А₁₆=7В.

С изменением основания системы счисления разрядность числа в ней изменяется. Если R_i - разрядность, то можно утверждать, что чем выше основание системы счисления, тем экономнее запись числа в памяти машины:

R₂>R₃>R₄>R₈>R₁₆.

Перевод правильной дроби из одной системы счисления в другую выполняется с помощью операции умножения. Для этого искомое число умножается на основание новой системы. Целая часть результата (но теперь уже в прямом направлении) формирует дробную часть числа в новой системе по очередному разряду после запятой, а дробная часть результата снова умножается на основание новой системы и т.д. Рассмотрим следующий пример.

П р и м е р. Перевести из десятеричной системы счисления число 0,25 (точное число) в двоичную систему.

0,25 ∙ 2 = 0 + 0,5; а_-1=0;

0,5 ∙ 2 = 1 + 0,0; а_-2=1.

Тогда дробное число А₁₀=0,25 должно быть записано в двоичной системе соответственно А₂=0,01. Выполним обратную проверку:

.

Мы получили число в десятеричной системе. Выполним перевод числа А₁₀=0,26 в двоичную систему:

0,26 ∙ 2 = 0 + 0,52; а_-1=0;

0,52 ∙ 2 = 1 + 0,04; а_-2=1;

0,04 ∙ 2 = 0 + 0,08; а_-3=0;

0,08 ∙ 2 = 0 + 0,16; а_-4=0.

Предположим, что процесс перевода на четвертом шаге прекращен. Тогда, выполняя проверку, переведем число А₂=0,0100 обратно в десятеричную систему счисления:

.

Но начальное значение А₁₀=0,26. Очевидна погрешность при переводе. Попробуем продолжить прерванный ранее процесс перевода:

0,16 ∙ 2 = 0 + 0,32; а_-5=0;

0,32 ∙ 2 = 0 + 0,64; а_-6=0;

0,64 ∙ 2 = 1 + 0,28; а_-7=1;

0,28 ∙ 2 = 0 + 0,56; а_-8=0;

0,56 ∙ 2 = 1 + 0,12; а_-9=1.

Видим, если взять семь разрядов после запятой, то получим А₂=0,0100001 и соответственно:

.

Если взять девять разрядов, то получим А₂=0,010000101 и соответственно:

.

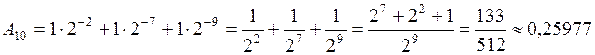В любом случае мы не получили точного значения А₁₀=0,26 и имеем погрешность. Это чрезвычайно важный вывод – при переводе дробной части числа из одной системы счисления в другую неизбежно появление погрешности (за исключением частных случаев, см. выше). Ее величина зависит от разрядности последней (справа) цифры. Если дробная часть числа А₂ составляет j знаков после запятой, то предельная абсолютная погрешность числа А₁₀ оценивается по выражению:

.

Действительно, из машины выведено число А₁₀=0,25780. Если в двоичной системе оно имело семь разрядов после запятой, тогда это число получено с абсолютной погрешностью:

.

Но если то же число получено при наличии девяти разрядов в двоичной системе, то абсолютная погрешность будет равна:

.

Погрешность всегда имеет знак «+», т.е. полученное число всегда меньше его точного значения.

Обратимся к элементарной информационной ячейке современных ЭВМ. Ее структура представлена на рисунке 2.1. Она включает:

- первичный элемент бит (технически это один триггер), который может иметь два состояния - отсутствие потенциала (это «ноль») и наличие потенциала (это «единица»);

- восемь бит образуют один байт;

- два байта образуют слово.

Рисунок 2.1. – Структура элементарной информационной ячейки

Ячейка из двух слов предназначена для хранения одного числа. Отсюда очевидно ограничение элементов памяти ЭВМ. Ниже будет показано, что при одинарной точности это ограничение оценивается 24 разрядами.

Безусловно, при увеличении количества разрядов перевода увеличивается точность представления дробной части числа. Если подвести итоги, можно констатировать следующее:

1) машинная технология работы с числами требует их преобразования в машинную систему счисления;

2) целые числа переводятся в машинную систему счисления с нулевой погрешностью;

3) дробная часть исходного числа всегда (за редким частным исключением) переводится в машинную систему счисления с погрешностью;

4) величина погрешности перевода зависит от принятой разрядности числа при его вторичном представлении в машинном коде;

5) так как машинная система счисления имеет собственное ограничение по разрядам, в ЭВМ принципиально невозможно получить абсолютно точные результаты арифметических процедур.

Date: 2016-07-18; view: 556; Нарушение авторских прав