
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Формы представления чисел в машине
|
|
В современных вычислительных машинах все числа могут быть представлены в двух формах: в естественной, которая носит название формы с фиксированной запятой (или точкой) и полулогарифмической, называемой еще формой с плавающей запятой (или точкой). При представлении чисел в естественной форме положение запятой, отделяющей целую часть от дробной, зафиксировано, т.е. жестко зафиксирован порядок чисел, с которыми оперирует машина. В настоящее время по этой схеме машины работают с числами, по модулю меньше единицы. Второй формой представления чисел в машине является полулогарифмическая. Любое вещественное число А, представленное в системе счисления с основанием «р», можно записать в виде:
 , (2.1)
, (2.1)
где М – мантисса;
k – порядок числа (целое число).
Например, десятичное число 234,47 или двоичное число 1011,01 можно представить следующим образом:
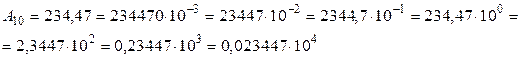

Заметим, что в структуре числа, представленного в двоичной системе счисления, множитель 102=210, а показатели степени соответственно эквивалентны -102=-210, 1002=410, 1012=510. Число, стоящее перед множителем, как известно, является мантиссой данного числа.
Видим, что, меняя положение запятой, всегда имеется возможность «загнать» мантиссу в нужный («удобный») разрядный ряд (например, сделать ее меньше единицы). В частности, в вычислительных машинах очень часто используются так называемые нормализованные числа, у которых в двоичной системе счисления мантисса всегда представляется числом п, в десятеричной системе лежащим в диапазоне 0,5 ≤ п ≤ 1.
Нормализация числа – преобразование его в удобную для работы форму методом унификации вида числа по выражению (2.1). В современных ЭВМ нормализация осуществляется по схеме:
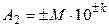 ,
,
где М – мантисса, записанная в двоичном коде;
k – порядок числа в двоичном коде (определяет, на сколько разрядов надо сдвинуть запятую).
Например, число А2=1011,01 в нормализованном виде будет иметь вид:
 ,
,
где степень 1002=410.
Формат представления числа в машине при одинарной точности представлен на рисунке 2.2. На все число отводится два слова с суммарным количеством разрядов, равным тридцати двум (два по шестнадцать).
Выше уже упоминалось о том, что в ЭВМ ограничено количество разрядов, отводимых для представления числа. Часть из этого лимита отводится для мантиссы, а часть для порядка. Наиболее важную часть информации содержит мантисса, так как именно она отображает цифровое содержание числа. Поэтому чем больше разрядов отводится для мантиссы, тем с большей точностью представляется число в ЭВМ. И чем больше разрядов занимает порядок, тем шире диапазон от наименьшего до наибольшего числа.

Рисунок 2.2 – Формат представления числа
В первом слове в 15 разряде указывается знак числа. Если оно положительное, то в ней фиксируется «0», если число отрицательное, то в этой ячейке стоит «1». Далее, разряды с 7 по 14 (всего восемь разрядов) отводится для фиксации порядка числа. Все остальные разряды, в том числе и во втором слове, отводятся для фиксации мантиссы числа.
В двоичном счислении порядок (максимальный) записывается числом  ,
,
т.е. в десятеричной системе это число 255.
Особо следует отметить формирование мантиссы. Согласно рисунку 2,2, мантиссе отводится (16+7=23) разряда. Однако с целью повышения точности числа это количество увеличено на единицу, т.е. мантиссе выделяется 24 разряда. Один дополнительный разряд образуется потому, что первая значащая цифра в мантиссе всегда равна единице. Поэтому в структуру памяти числа ее не вносят, но при вычислениях всегда учитывают. Теперь можно рассчитать максимальное значение мантиссы:
 .
.
Тогда максимальное число, которое можно зафиксировать в памяти машины, будет следующим:
 .
.
Это чрезвычайно большое число, намного превышающее так называемое мировое число  , которое свидетельствует, что во вселенной нет ничего, что, будучи просчитанным количественно, потребует числа больше мирового. Поэтому, в силу значительности
, которое свидетельствует, что во вселенной нет ничего, что, будучи просчитанным количественно, потребует числа больше мирового. Поэтому, в силу значительности  и так как следует предусмотреть и знак порядка (± k), в ЭВМ при нормализации числа используется обратное кодирование или кодирование порядка со смещением. Это означает, что, если k=0, то в разряды порядка заносится число 12810 или 100000002. Тогда, если k > 0, записывается число
и так как следует предусмотреть и знак порядка (± k), в ЭВМ при нормализации числа используется обратное кодирование или кодирование порядка со смещением. Это означает, что, если k=0, то в разряды порядка заносится число 12810 или 100000002. Тогда, если k > 0, записывается число
k1 = 128 + k > 128
и, соответственно, 128 < k1 < 255, а максимальное значение kmax = (255-127)=127. Если k < 0, то k1 = 128 - k < 128 и kmin= -128.
Поэтому, например, число А10= - 49,5 будет иметь следующий формат:
- 49,510 = - 110001,1002 = - 0,11000112 ∙ 10110.
Но, на основании вышесказанного
k = 610 = (6 + 128)10; k1 = (134)10 = 100001102.
Тогда число А10 = - 49,5 поразрядно будет иметь вид, представленный на рисунке 2.3.

Рисунок 2.3 – Формат числа -49,5
Минимальное значение мантиссы равно 0,12, что в десятеричной системе счисления эквивалентно 0,510. Но если все разряды мантиссы заполнить единицами, то ее максимальное значение в десятеричной системе будет равно единице. Именно поэтому  .
.
Форма представления числа с плавающей запятой добавляет сложности в процесс вычислений, так как каждый раз следует преобразование вида числа. Но зато применение этой схемы форматирования позволяет автоматически масштабировать число, не вызывает накопления абсолютной погрешности вычисления (но не избавляет от накопления относительной погрешности).
Date: 2016-07-18; view: 500; Нарушение авторских прав