
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Теоретические положения
|
|
Цель работы
Изучить основы календарно-сетевого планирования. Получить навыки анализа сетевых графиков и определения критических путей.
Теоретические положения
Календарно-сетевое планирование представляет собой важную задачу, стоящую перед любым предприятием или организацией. Специализированное программное обеспечение, предназначенное для решения задач календарно-сетевого планирования, является широко востребованным и довольно дорогостоящим. Наибольшей популярностью в этой сфере пользуется ПО, предоставляющее возможности для решения задач календарно-сетевого планирования в комплексе с оптимизацией графиков по различным параметрам и другими методами, которые в совокупности называются методами управления проектами.
Речь идет об управлении сложными разветвленными комплексами работ, различным образом связанными друг с другом, и приводящими к достижению некоторой цели, т.е. имеющими завершающее событие, конец. Для управления такими сложными комплексами работ существует специальный метод, называемый сетевое планирование.
Сетевое планирование – это метод управления, основанный на использовании математического аппарата теории графов для отображения и алгоритмизации комплексов взаимосвязанных работ, действий или мероприятий для достижения четко поставленной цели.
Используя методы сетевого планирования мы можем:
- выбрать наилучший план из всех возможных вариантов;
- определить критически важные работы, задержка которых приведет к задержке всего плана;
- оценить резервы т.н. напряженных работ;
- распределить оборудование и людей по работам (операциям) и провести оптимизацию графика с точки зрения наличия и необходимости ресурсов;
- при необходимости проводить оптимизацию графика по другим параметрам (материалам, финансированию и др.)
- своевременно контролировать и корректировать ход выполнения работ.
Основная цель сетевого планирования – сокращение до минимума продолжительности выполнения сложного комплекса работ.
Все работы чаще всего измеряются в рабочих днях или часах. Однако далеко не все работы могут выполняться в любое время суток. Это связано, в том числе, и с работой ресурсов, которые эти работы выполняют. Поэтому все сетевые графики имеют связь с календарными ограничениями, или говорят просто, календарями, т.е. периодами рабочего времени. Поэтому часто используют название методы календарно-сетевого планирования.
Причем, календарей, как и самих ресурсов, может быть много. Поэтому следует сказать, что если методы сетевого планирования вполне можно использовать вручную, без применения специализированных средств, то календарно-сетевое планирование реализовать без специализированного ПО практически невозможно.
Календарное сетевое планирование базируется на использовании сетевых графиков (сетевых моделей), математический аппарат которых, в свою очередь, базируются на теории графов.
Сетевая модель представляет собой граф вида «сеть», в которой моделируется совокупность взаимосвязанных работ (операций) и событий, отображающих процесс достижения определенной цели. На рис. 1 представлена сетевая модель, состоящая из 11 событий и 16 работ, длительность выполнения которых указана НАД работами. Такой вид сетевой модели относится к типу «операции на дугах».
Работа (операция) характеризует материальное действие, требующее использования ресурсов, или логическое действие, требующее лишь взаимосвязи событий. При графическом представлении работа изображается стрелкой, которая соединяет два события. Она обозначается парой заключенных в скобки чисел (i,j), где i — номер события, из которого работа выходит, а j — номер события, в которое она входит. Работа не может начаться раньше, чем свершится событие, из которого она выходит.

Рис. 1. Сетевая модель.
Каждая работа имеет определенную продолжительность  . Например, запись t (2,5) = 4 означает, что работа (2,5) имеет продолжительность 4 единицы (дня или часа). К работам относятся также такие процессы, которые не требуют ни ресурсов, ни времени выполнения. Они заключаются в установлении логической взаимосвязи работ и показывают, что одна из них непосредственно зависит от другой; такие работы называются фиктивными и на графике изображаются пунктирными стрелками (см. работу (6,9)).
. Например, запись t (2,5) = 4 означает, что работа (2,5) имеет продолжительность 4 единицы (дня или часа). К работам относятся также такие процессы, которые не требуют ни ресурсов, ни времени выполнения. Они заключаются в установлении логической взаимосвязи работ и показывают, что одна из них непосредственно зависит от другой; такие работы называются фиктивными и на графике изображаются пунктирными стрелками (см. работу (6,9)).
Событиями называются результаты выполнения одной или нескольких работ (начало или окончание работы). Они не имеют протяженности во времени. Событие свершается в тот момент, когда оканчивается последняя из работ, входящая в него. События обозначаются одним числом и при графическом представлении изображаются кружком, внутри которого проставляется его порядковый номер (i = 1, 2,..., n).
В сетевой модели имеется начальное (исходное) событие (с номером 1), из которого работы только выходят, и конечное (завершающее) событие (с номером N), в которое работы только входят.
Любая последовательность работ в сети, в которой конечное событие каждой работы последовательности совпадает с начальным событием следующей за ней работы, называется путем.
Полный путь — это цепочка (непрерывная последовательность) следующих друг за другом работ, соединяющих начальную и конечную вершины, например, в приведенной выше модели путями являются L 1= (1, 2, 3, 7, 10, 11), L 2= (1, 2, 4, 6, 11) и др.
Продолжительность пути определяется суммой продолжительностей составляющих его работ. Полный путь, имеющий максимальную длину, называют критическим и обозначают L Kp, а его продолжительность — T кр. Работы, принадлежащие критическому пути, называются критическими. Их несвоевременное выполнение ведет к срыву сроков всего комплекса работ. На сетевом графике критический путь изображается двойной стрелкой.
Сетевая модель имеет ряд характеристик, которые позволяют определить степень напряженности выполнения отдельных работ, а также всего их комплекса и принять решение о перераспределении ресурсов.

Рис. 2. Ошибки сетевой модели.
Перед расчетом сетевой модели следует убедиться, что она удовлетворяет следующим основным требованиям:
1. События правильно пронумерованы, т. е. для каждой работы (i, j) i < j (см. на рис. 2. работы (4,3) и (3,2)).
2. Отсутствуют тупиковые события (кроме завершающего), т. е. такие, за которыми не следует хотя бы одна работа (событие 5 из рис. 2);
3. Отсутствуют события (за исключением исходного), которым не предшествует хотя бы одна работа (событие 7);
4. Отсутствуют циклы, т. е. замкнутые пути, соединяющие событие с ним же самим (см. путь (2,4,3)).
5. Все события соединяются только одной стрелкой.
В табл.1 определены продолжительности полных путей. Выделенный жирным путь имеет наибольшую продолжительность и, предположительно, является критическим. Любая задержка в выполнении работ, лежащих на критическом пути, нарушает сроки выполнения всего комплекса работ. Работы, не лежащие на критическом пути, допускают определенную задержку во времени выполнения, которая не сказывается на сроках выполнения всего комплекса работ. Это называется резерв.
Для того чтобы рассчитать резервы времени, необходимо ввести временные характеристики событий. Основными временными параметрами сетей являются ранние и поздние сроки наступления событий. Зная их, можно вычислить остальные параметры сети – сроки начала и окончания работ и резервы времени событий и работ. На рис. 3 изображены ранние и поздние сроки событий для работы (i, j).
Таблица 1. Продолжительности полных путей.
| Вид полного пути | Продолжительность пути T |
| 1-2-3-7-10-11 | 6+5+1+6+9=27 |
| 1-2-5-8-10-11 | 6+4+3+4+9=26 |
| 1-2-5-10-11 | 6+4+9+9=28 |
| 1-2-4-5-8-10-11 | 6+3+6+3+4+9=31 |
| 1-2-4-5-10-11 | 6+3+6+9+9=33 |
| 1-2-4-9-10-11 | 6+3+7+3+9=28 |
| 1-2-4-6-9-10-11 | 6+3+4+0+3+9=25 |
| 1-2-4-6-11 | 6+3+4+5=18 |

Рис. 3. Обозначения ранних и поздних сроков событий.
Ранний возможный срок наступления j -го события определяется величиной наиболее длительного отрезка пути от исходного до рассматриваемого события. Причем, 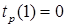 , а
, а  . Ранний срок наступления j -го события определяется по формуле:
. Ранний срок наступления j -го события определяется по формуле:
 . (1)
. (1)
Поздний допустимый срок наступления i -го события это самый поздний срок, который не нарушает поздних допустимых сроков следующих за ним событий. Т.е. это время, необходимое для выполнения всех работ, происходящих после наступления i -го события. Причем,  . Поздний срок наступления i -го события определяется по формуле:
. Поздний срок наступления i -го события определяется по формуле:
 . (2)
. (2)
Поздние сроки определяются «обратным ходом», начиная с завершающего события.
Рассчитаем ранние сроки событий для рассматриваемого примера.
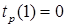 ,
,
 ,
,
 ,
,
 ,
,
 ,
,
 ,
,
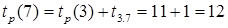 ,
,
 ,
,
 ,
,
 ,
,
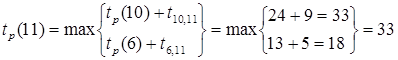 .
.
Рассчитаем поздние сроки событий для рассматриваемого примера.
 ,
,
 ,
,
 ,
,
 ,
,
 ,
,
 ,
,
 ,
,
 ,
,
 ,
,
 ,
,
 .
.
У работ, лежащих на критическом пути, ранние и поздние сроки событий совпадают. На графике такие события обводятся двойным кружком. Но совпадение ранних и поздних сроков наступления событий для определения критического пути является условием необходимым, но не достаточным (это условие не дает однозначного определения критического пути). Для однозначного определения критического пути необходимо рассчитать резервы времени выполнения работ. Всего существует четыре вида резерва времени выполнения работы (i, j).
Полный резерв времени показывает, на сколько можно увеличить время выполнения конкретной работы при условии, что срок выполнения всего комплекса работ не изменится. Полный резерв вычисляется по формуле:
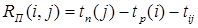 . (3)
. (3)
Гарантийный резерв – это часть полного резерва, на которую можно увеличить продолжительность работы, не изменив при этом позднего срока ее начального события. Гарантийный резерв вычисляется по формуле:
 . (4)
. (4)
Свободный резерв – это часть полного резерва времени, на которую можно увеличить продолжительность работы, не изменив при этом раннего срока ее конечного события. Свободный резерв вычисляется по формуле:
 . (5)
. (5)
Независимый резерв – соответствует случаю, когда все предшествующие работы заканчиваются в поздние сроки, а все последующие начинаются в ранние сроки. Использование этого резерва не влияет на величину резервов времени других работ. Независимый резерв вычисляется по формуле:
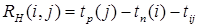 . (6)
. (6)
Для работ, лежащих на критическом пути, все четыре вида резервов времени равны нулю. Если какой-либо резерв времени оказывается отрицательным, то его полагают равным нулю. С помощью критических работ, т.е. работ, не имеющих резервов времени, определяется критический путь сетевого графика. Этот способ эффективен, когда сеть содержит несколько критических путей.
Для расчета временных резервов рассматриваемого примера создадим таблицу 2. У операций критического пути все резервы равны нулю.
Таблица 2. Расчет резервов времени.
| Работа (i, j) | Длительность, 
| Начало работы | Окончание работы | Резервы времени | |||||
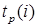
| 
| 
| 
| RП (6-3-2) | RГ (6-4-2) | RС (5-3-2) | RН (5-4-2) | ||
| 1,2 | |||||||||
| 2,3 | |||||||||
| 2,4 | |||||||||
| 2,5 | |||||||||
| 3,7 | 0(отр) | ||||||||
| 4,5 | |||||||||
| 4,6 | |||||||||
| 4,9 | |||||||||
| 5,8 | |||||||||
| 5,10 | |||||||||
| 6,9 | 0(отр) | ||||||||
| 6,11 | |||||||||
| 7,10 | |||||||||
| 8,10 | |||||||||
| 9,10 | |||||||||
| 10,11 |
Date: 2016-07-18; view: 401; Нарушение авторских прав