Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Основные термины и определения сопромата
|
|
Сопротивление материала – это наука, дающая основы для расчётов на прочность, жёсткость и устойчивость.
Прочность – это способность выдерживать внешнюю нагрузку, не разрушаясь.
Жёсткость– это способность сопротивляться изменению первоначальной формы и размера.
Устойчивость – это способность сохранять первоначальную форму равновесия.
Сопромат внешних активных сил принято называть нагрузкой. Нагрузки классифицируется:
1) По способу приложения:
1.1 объёмные
1.2 поверхностные
1.2.1 распределённые
а) по площади
б) по линии
1.2.2 сосредоточенные
а) сила
б) момент
2) По характеру взаимодействия
2.1 статические - изменяется от 0 до конечно значения
2.2 динамические – мгновенно приложенный удар повторно-переменный.
Все эти виды нагрузок вызывают деформацию. Основные виды деформации сложные, однако их можно представить состоящими из небольшого числа основных:
1.Растяжение (сжатие)
2.Сдвиг (срез)
3.Кручение
4.Изгиб
Элементы конструкции, которые воспринимают деформацию имеют как правило сложную форму, но их можно представить в виде простых составных элементов, для которых выполняются расчёты сопромата.
Брус – это элемент конструкции, у которого длина намного больше поперечных размеров. Бывают прямолинейные и криволинейные. Линия, проходящая через центр масс поперечного сечения бруса, называется осевой. Груз с прямой осью называют стержнем. Основные характеристик бруса: длина и размер поперечного сечения.
Оболочка – элемент конструкции, ограниченный параллельными поверхностями, расположенными на близком расстоянии. Плоские оболочки называю плитами и пластинами.
Массивное тело – элемент конструкции, у которого высота, длин и ширина одного порядка.
Основные гипотезы и допущения:
1Гипотеза о сплошном строении материала.
2Материал полностью заполняет объём тела и пустоты в нём отсутствуют.
3. Гипотеза об однородности материала. Частицы материала обладают одинаковыми свойствами, которые не зависят от размеров тела.
4. Гипотеза об изотропности материала. Свойство материала в любых направлениях одинаково (древесина – анизотропный)
5. Гипотеза плоских сечений. Поперечное сечение остаётся плоским и нормальным к оси до и после приложения нагрузки.
Допущения: 1) деформация на столько меньше размеров тел, что не оказывает влияния на расположение тел 2) допущение о линейной зависимости между деформацией и нагрузкой.
Внешние силы
Внешняя сила — это мера взаимодействия между телами. В задачах сопротивления материалов внешние силы считаются всегда заданными
Поверхностные силы делятся на сосредоточенные и распределенные.
Сосредоточенными считаются силы, приложенные к малой поверхности, размеры которой малы по сравнению с размерами тела
Распределенные нагрузки бывают распределенными по длине и по площади. К распределенным нагрузкам относят давление жидкости, газа или другого тела
Статическими считаются нагрузки, в процессе приложения которых возникающие силы инерции малы и ими можно пренебречь
Внутренние силы
В результате действия внешних сил в теле возникают внутренние силы.
Внутренняя сила — силы взаимодействия между частями одного тела, возникающие под действием внешних сил.
Внутренние силы являются самоуравновешенными, поэтому они не видны и не влияют на равновесие тела. Определяют внутренние силы методом сечения.
Внешние нагрузки приводят к следующим видам напряженно-деформированного состояния:
Срез
Изгиб
Кручение
| Метод сечений. |
| Так как внутренние силы взаимно уравновешены и стоит задача выразить их через внешние, то необходимо выполнить такую операцию, чтобы внутренние силы стали явными. |
| Например для стержня можно применить прием мысленного рассечения на две части плоскостью, перпендикулярной продольной оси. Затем отбросить одну из полученных частей, что позволяет превратить внутренние силы, для целого стержня, во внешние для оставленной части стержня |
В сопромате различают несколько простейших видов нагружения и несколько сложных. К простейшим относятся следующие.
Растяжение (сжатие) возникает в случае, когда стержень нагружен силами, совпадающими по направлению с его осью (рис. 1.19).

Рис. 1.19
В этом случае из шести внутренних силовых факторов пять равны нулю и только продольная сила N # 0 (рис.1.16).
На растяжение, сжатие работают многие элементы конструкций: стержни ферм, колонны, штоки паровых машин и поршневых насосов, стяжные винты и другие детали.
Сдвиг или срез возникает, когда внешние силы смещают два параллельных сечения одно относительно другого, при неизменном (рис.1 20) расстоянии между ними.
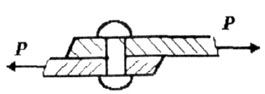
Рис 1.20
На сдвиг или срез работают, например, заклепки или болты, скрепляющие элементы, которые силы пытаются сдвинуть.
Кручение возникает при действии на стержень внешних сил, образующих моменты относительно продопьной оси стержня. Из шести внутренних сил только Мкр # 0. На кручение работают вапы. шпиндели токарных и сверлипьных станков и др. детали (рис.1.21)

Рис. 1.21
Изгиб - это такой вид нагружения, когда внешние силы вызывают моменты относительно оси симметрии (или главной оси), расположенной в плоскости поперечного сечения. Этот момент называется изгибающим. Самый простой случай - это плоский изгиб, когда все внешние силы лежат в одной плоскости, совпадающей во всех рассматриваемых нами случаях с ппоскостью симметрии (или главной ппоскостью) балки.
| |||||||||||||||||
|
| Кручение. | |||||||||||||||||||||||||||||||||||||
| Кручением называется такой вид деформации, при котором в поперечном сечении вала возникает только крутящий момент Мкр, а все остальные внутренние силовые факторы равны нулю. | |||||||||||||||||||||||||||||||||||||
| Уравнение равновесия: | |||||||||||||||||||||||||||||||||||||

| |||||||||||||||||||||||||||||||||||||
| Деформация - угол сдвига (рис, 3.2) | |||||||||||||||||||||||||||||||||||||
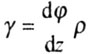
| |||||||||||||||||||||||||||||||||||||
| Напряжения | |||||||||||||||||||||||||||||||||||||

| |||||||||||||||||||||||||||||||||||||
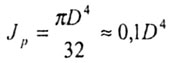 - полярный момент инерции; - полярный момент инерции;
| |||||||||||||||||||||||||||||||||||||
| D - диаметр стержня круглого поперечного сечения, | |||||||||||||||||||||||||||||||||||||
 - касательные напряжения, р • расстояние от точки, где определяется - касательные напряжения, р • расстояние от точки, где определяется  до центра вала. до центра вала.
| |||||||||||||||||||||||||||||||||||||
| Угол закручивания элемента | |||||||||||||||||||||||||||||||||||||
 - модуль упругости второго рода - модуль упругости второго рода
| |||||||||||||||||||||||||||||||||||||
| Угол закручивания стержня | |||||||||||||||||||||||||||||||||||||

| |||||||||||||||||||||||||||||||||||||
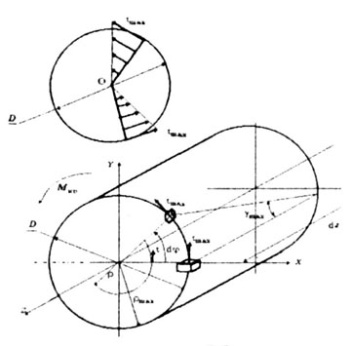
Напряженное состояние - чистый сдвиг (рис.3.1). 
| |||||||||||||||||||||||||||||||||||||
| Рис. 3.1 | |||||||||||||||||||||||||||||||||||||
| |||||||||||||||||||||||||||||||||||||
| Рис. 3.2 | |||||||||||||||||||||||||||||||||||||
| Условие прочности: | |||||||||||||||||||||||||||||||||||||

| |||||||||||||||||||||||||||||||||||||
| Для хрупких материалов: | |||||||||||||||||||||||||||||||||||||

| |||||||||||||||||||||||||||||||||||||
| Для пластических материалов: | |||||||||||||||||||||||||||||||||||||
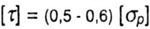
| |||||||||||||||||||||||||||||||||||||
| Условие жесткости: | |||||||||||||||||||||||||||||||||||||
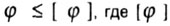 - допускаемый угол закручивания - допускаемый угол закручивания
|
| Растяжени | Кручение** | Изгиб*** |

| 
| 
|

| 
| 
|
Date: 2016-07-18; view: 963; Нарушение авторских прав
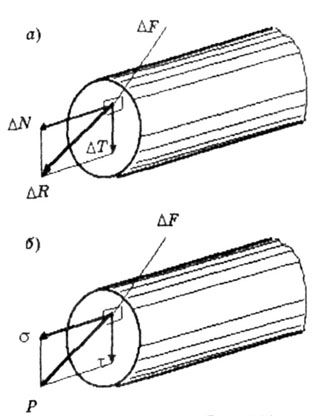

 (сигма) - нормальное напряжение, действует по нормали (перпендикуляру) к площадке;
(сигма) - нормальное напряжение, действует по нормали (перпендикуляру) к площадке;
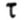 (тау) - касательные напряжения, они скользят по площадке, касаются ее (рис. 1.15).
(тау) - касательные напряжения, они скользят по площадке, касаются ее (рис. 1.15).