
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Перевод чисел из одной позиционной системы счисления в другую.
|
|
Перевод числа из исходной позиционной системы счисления (ПСС) в новую осуществляется расчетом нового значения этого числа, т.е. его значения в новой ПСС. В расчетах участвуют:
- исходное число;
- основание новой ПСС.
Расчеты производятся по правилам арифметики исходной ПСС.
Различают алгоритмы перевода:
- целых чисел;
- правильных дробей;
- действительных чисел.
Для перевода целого числа необходимо последовательно делить число и получаемые целые частные на основание новой ПСС до тех пор, пока не получится частное, меньшее делителя. Последнее частное и полученные остатки являются цифрами числа в новой ПСС. Число в новой ПСС составляется из этих цифр, начиная с последней цифры.
Пример. Перевести число  из исходной ПСС (т.е. десятичной СС) в двоичную.
из исходной ПСС (т.е. десятичной СС) в двоичную.

Т.о., 
Для перевода правильной дроби необходимо последовательно умножать число и получаемые дробные части произведения на основание новой ПСС до тех пор, пока дробная часть произведения не станет равное 0 или не будет достигнута требуемая точность перевода. Полученные целые части произведений являются цифрами дробной части числа в новой ПСС. Дробная часть числа в новой ПСС составляется из этих цифр, начиная с первой цифры.
Пример. Перевести число  из исходной ПСС (т.е. десятичной СС) в двоичную.
из исходной ПСС (т.е. десятичной СС) в двоичную.

Т.о., 
Т.к. любое действительное число можно представить как сумму целого числа и правильной дроби, то перевод этого числа в новую ПСС осуществляется в два этапа. Отдельно переводится целая часть числа (по алгоритму перевода целых чисел), отдельно − дробная часть числа (по алгоритму перевода правильных дробей). Полученные значения складываются.
Пример. Перевести число  из исходной ПСС (т.е. десятичной СС) в двоичную. Представим число как сумму целого числа и правильной дроби:
из исходной ПСС (т.е. десятичной СС) в двоичную. Представим число как сумму целого числа и правильной дроби:  .
.

Т.о., 
Возврат к исходной ПСС осуществляется путем представления нового числа в виде полинома и вычислении его значения по правилам исходной ПСС.
Пример. Перевести числа предыдущих примеров из двоичной ПСС в исходную, десятичную.
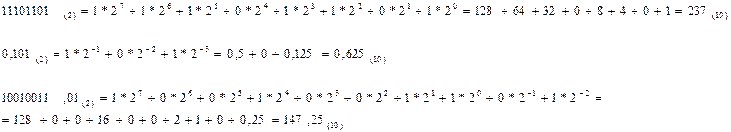
При переводе чисел из двоичной ПСС в ПСС с основанием, кратным 2-м, и обратно используются более простые алгоритмы. Проиллюстрируем это на примере восьмеричной и шестнадцатеричной ПСС.
Т.к.  , то каждая цифра восьмеричной ПСС кодируется триадой двоичных цифр:
, то каждая цифра восьмеричной ПСС кодируется триадой двоичных цифр:
| Цифры восьмеричной ПСС | Триады двоичных цифр |
Т.к.  , то каждая цифра шестнадцатеричной ПСС кодируется тетрадой двоичных цифр:
, то каждая цифра шестнадцатеричной ПСС кодируется тетрадой двоичных цифр:
| Цифры шестнадцатеричной ПСС | Тетрады двоичных цифр |
| A | |
| B | |
| C | |
| D | |
| E | |
| F |
При переводе числа из 8-ной (16-ной) ПСС в 2-ную каждую цифру исходного числа заменяют соответствующей триадой (тетрадой).
Пример. Перевести числа из исходной в 2-ную ПСС.

Перевод двоичного числа в 8-ную (16-ную) ПСС также выполняется по триадам (тетрадам). Двоичное число разбивают на триады (тетрады): целую часть числа − справа налево, дробную − слева направо. Если в последних группах окажется меньше 3-х (4-х) цифр, то их дополняют нулями. Полученные триады (тетрады) заменяют цифрами соответствующей ПСС.
Пример. Перевести числа из 2-ной в указанную ПСС.

Date: 2016-11-17; view: 673; Нарушение авторских прав