
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Меры и единицы количества и объема информации.
|
|
Существует несколько подходов к измерению информации. Наиболее популярными являются:
- объемный (синтаксический);
- вероятностный (энтропийный);
- алгоритмический;
- аксиологический;
- семантический.
Объемный подход является самым простым. В этом случае оперируют «обезличенной» информацией, т.е. без учета ее смыслового содержания. Количественную оценку информации при этом называют объемом информации. Объем информации − это количество символов в информационном сообщении.
Данный способ измерения чувствителен к форме представления сообщения.
Пример:
| Форма представления | Сообщение | Объем информации |
| Десятичная система счисления | 21(10) | 2 символа |
| Двоичная система счисления | 11001(2) | 5 символов |
| Римская система счисления | XXI | 3 символа |
| Текстовое представление | Двадцать один | 13 символов |
В вычислительной технике все обрабатываемые данные представлены в двоичном коде. Поэтому минимальной единицей объема информации является 1 бит (от англ. bit − binary digit, двоичная цифра). Более крупной единицей является 1 байт: 1 байт=8 бит. Для измерения больших объемов информации используют производные единицы, обозначаемые с помощью приставок:
- кило → К → 210 = 1024
- мега → М → 220
- гига → Г → 230
- тера → Т → 240
- пета → П → 250
- экса → Э → 260
- зета → З → 270
- йота → Й → 280
Пример: 1 Кбайт = 210 байт = 1024 байт
5 Кбит = 5*210 бит = 5*1024 бит = 5120 бит
Производные единицы взаимосвязаны:
Пример: 1 Мбайт = 210 Кбайт; 1 Гбайт = 210 Мбайт; 1 Тбайт =210 Гбайт
Вероятностный подход связывает количество информации с содержанием информации. Сообщение информативно, т.е. содержит ненулевую информацию, если оно пополняет знания человека. Информацию можно считать мерой уменьшения неопределенности о возможности наступления некоторых событий. Общая мера неопределенности (энтропия) характеризуется некоторой математической зависимостью от совокупности вероятностей этих событий. Т.о. количество информации в сообщении определяется тем, насколько уменьшилась эта мера после получения сообщения.
Рассмотрим в качестве примера опыт, связанный с бросанием правильной игральной кости, имеющей N граней (наиболее распространенным является случай шестигранной кости: N = 6). Результатом данного опыта может быть выпадение грани с одним из следующих знаков: 1, 2,..., N.
Введем в рассмотрение численную величину, измеряющую неопределенность — энтропию (обозначим ее H). Величины N и H связаны между собой некоторой функциональной зависимостью: 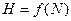 , а сама функция f является возрастающей, неотрицательной и определенной (в рассматриваемом нами примере) для N =1,2,..., 6.
, а сама функция f является возрастающей, неотрицательной и определенной (в рассматриваемом нами примере) для N =1,2,..., 6.
Рассмотрим процедуру бросания кости более подробно:
1) готовимся бросить кость; исход опыта неизвестен, т.е. имеется некоторая неопределенность; обозначим ее H1;
2) кость брошена; информация об исходе данного опыта получена; обозначим количество этой информации через I;
3) обозначим неопределенность данного опыта после его осуществления через H2.
За количество информации, которое получено в ходе осуществления опыта, примем разность неопределенностей «до» и «после» опыта: 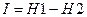
Очевидно, что в случае, когда получен конкретный результат, имевшаяся неопределенность снята (Н2 = 0), и, таким образом, количество полученной информации совпадает с первоначальной энтропией. Иначе говоря, неопределенность, заключенная в опыте, совпадает с информацией об исходе этого опыта.
Количество информации − это числовая характеристика информации, отражающая ту степень неопределенности, которая исчезает после получения информации.
Пусть потенциально может осуществиться некоторое множество событий − N, каждое из которых может произойти с вероятностью Pi. Тогда:
 − формула Шеннона.
− формула Шеннона.
Если события равновероятны, то 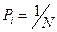 . Тогда
. Тогда 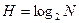 − формула Хартли.
− формула Хартли.
Важным при введении какой-либо величины является вопрос о том, что принимать за единицу ее измерения. Очевидно, Н будет равно единице при N = 2. Иначе говоря, в качестве единицы принимается количество информации, связанное с проведением опыта, состоящего в получении одного из двух равновероятных исходов (примером такого опыта может служить бросание монеты, при котором возможны два исхода: «орел» и «решка»). Такая единица количества информации называется «бит».
Между вероятностным и объемным количеством информации соотношение неоднозначное. Далеко не всякое сообщение, записанное двоичными символами, допускает измерение количества информации в энтропийном смысле, но всегда допускает его измерение в объемном смысле. Далее, если некоторое сообщение допускает измеримость количества информации в обоих смыслах, то они не обязательно совпадают, при этом энтропийное количество информации не может быть больше объемного.
В алгоритмической теории информации (раздел теории алгоритмов) используют алгоритмический метод оценки информации: любому сообщению приписывают количественную характеристику, отражающую сложность (размер) программы, которая позволяет его воспроизвести. Т.к. существует много разных вычислительных машин и разных языков программирования, то для определенности задаются некоторой конкретной машиной (например, машиной Тьюринга).
При анализе информации социального (в широком смысле) происхождения на первый план могут выступать такие ее свойства, как достоверность, актуальность, полнота и т.д. Их невозможно оценить н уменьшением неопределенности (вероятностный подход), ни числом символов (объемный подход). Обращение к качественной стороне информации породило новые подходы к ее оценке.
При аксиологическом подходе стремятся исходить их ценности, практической значимости информации, т.е. качественных характеристик, значимых в социальной системе.
При семантическом подходе информация рассматривается с точки зрения как формы, так и ее содержания. При этом информацию связывают с тезаурусом, т.е. полнотой систематизированного набора данных о предмете информации.
Указанные подходы не исключают количественного анализа, но он становится существенно сложнее и должен базироваться на современных методах математической статистики.
Date: 2016-11-17; view: 1258; Нарушение авторских прав