Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?
Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника
Вычисление площади плоских фигур в декартовой системе координат.
|
|
Рассмотрим криволинейную трапецию, ограниченную прямыми
x=a, x=b, y=0 и кривой y=f(x), где f(x) ³ 0.
Как известно, площадь такой криволинейной трапеции выражается через определенный интеграл: S = 
Пример: Вычислить площадь фигуры, ограниченной линиями y=e2x, x=0, x=2, y=0
S = 
= 
= 
.
Замечание: Иногда криволинейную трапецию приходится разбивать на несколько частей. Площадь всей трапеции есть сумма площадей всех частей.
Пример: Вычислить площадь фигуры, ограниченной линиями y=x, xy=1(y=1/x), x=0, x=2, y=0.
Разобьем трапецию на две части S1 и S2.
Площадь всей трапеции: S=S1+S2 = 
= 
= = 
.
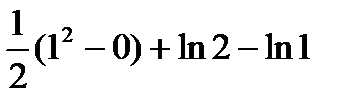В общем случае площадь фигуры, ограниченной слева прямой x=a, справа прямой x=b, сверху кривой y=f2(x), снизу кривой y=f1(x), причем f2(x) ³f1(x).
В этом случае, неважно, где лежит криволинейная трапеция, выше оси OX или ниже, или часть выше, часть ниже. Самое главное, чтобы выполнялось f2(x) ³f1(x).
Date: 2016-11-17; view: 636; Нарушение авторских прав