Два этапа решения диофантовых уравнений

Процесс нахождения целочисленного решения распадается на 2 этапа:

I. Доказательство того, что уравнение (1) имеет частное решение и указание способов получения этого решения.

II. Нахождение общего решения.

I этап. Нахождение ч астных решений.

Отыскание целочисленного решения тесно связано с решением сравнений.

Теорема 2. Если (х₀, у₀) – целочисленное решение уравнения (1), а 0, b 0, то х₀- решение уравнения .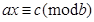

Обратно, если х₀ – решение сравнения (4), то существует , что (х₀, у₀) – решение неопределенного уравнения (1).

Доказательство: 1) пусть (х₀, у₀) – одно из целочисленных решений уравнения ах+bу=с ах - с= -by₀ b ax₀ c(mod b) x₀ – решение срав. (4).

2) пусть х₀ – решение сравнения (4) , где у₀ - целочисленное решение уравнения ах+bу=с.

В частности, из полученных выше утверждений о сравнениях 1 степени получаем:

Следствие 1:

Если (а,b)=d, то неопределенное целочисленное решение ах+bу=с, имеет целочисленное решение

Нахождение частного решения с помощью линейного представления НОД:

Рассмотрим ах+bу=1.

Обозначим х₀, у₀ – его решениями. Если (а,b)=1 , что выполняется ах+bу=1, частное решение неопределенного уравнения (*) примет вид (х₀с, у₀с).

II этап: нахождение общего решения.

Теорема 3. Если неопределенное уравнение (*) с целыми коэффициентами, где (а, b)=1, имеет частное целочисленное решение (х₀, у₀), то общее решение этого уравнения имеет вид

(**) {

Доказательство: 1) покажем, сначала, что при целом формулы (**) дают некоторое решение неопределенного уравнения (*),

Пусть t – какое-либо целое число

Непосредственная проверка показывает, что а(х₀+bt)+

+b(y₀-at)=ax₀+by₀=c, т.к. (х₀, у₀) – одно из решений уравнения (*).

2. Обратно, решение неопределенного уравнения (*) может быть записано в виде формулы (**), т.е. эти исчерпываются все целочисленные решения уравнения (*).

Пусть (х₁, у₁) – произвольное решение уравнения (*), тогда

ах₁+bу₁=с и ах₀+bу₀=с,

а(х₀-х₁)+b(y₀-y₁)=0

а(х₀-х₁)=-b(y₀-y₁)

и (а, b)=1

,

Подставляем найденное значение у₁ в (5), получим а(х₀-х₁)=-bat

x₁=x₀+bt, теорема доказана.

Литература: 1, стр 211, 2; стр 224, 294; 3; стр 146

Контрольные вопросы:

1. Дайте определение неопределённого уравнения первой степени с двумя неизвестными.

2. Какие диофантовы уравнения называются однородными и неоднородными?

3. Что называется частным решением неопределённого уравнения?

4. Укажите 2 этапа решения диофантовых уравнений.

Date: 2016-11-17; view: 388; Нарушение авторских прав