
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

НОД. Алгоритм Евклида. НОК
|
|
Определение 3. Всякое целое число  0, делящее одновременно целые
0, делящее одновременно целые  ,...,
,..., 
 над общим делителем этих чисел.
над общим делителем этих чисел.
Определение 4. Общий делитель  целых чисел
целых чисел  ,...,
,...,  называется наибольшим общим делителем, если он делится на всякий общий делитель этих чисел, т. е.
называется наибольшим общим делителем, если он делится на всякий общий делитель этих чисел, т. е.
1) 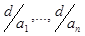
2) 
 .
.
Предложение. НОД чисел  ,...,
,...,  определен однозначно с точностью до знака (т.е. если
определен однозначно с точностью до знака (т.е. если  – НОД чисел
– НОД чисел  ,...,
,...,  , то –
, то –  – тоже НОД этих чисел).
– тоже НОД этих чисел).
Доказательство: пусть  ,
,  - НОД чисел
- НОД чисел  ,...,
,..., 



 и
и 

 (т. к. НОД делится на
(т. к. НОД делится на  общий делитель этих чисел)
общий делитель этих чисел) 
 =
= 
 или
или  = -
= -  .
.
В дальнейшем условимся рассматривать только положительные значения НОД и обозначать  = (
= ( ,...,
,...,  ).
).
Для нахождения НОД существует алгоритм, который был дан Евклидом. Описав способ нахождения НОД, мы доказываем тем самым существование НОД.
Алгоритм Евклида базируется на следующих леммах:
Лемма 1. Если 

 , то (
, то ( ,
,  ) =
) = 
Доказательство: 1)  и
и 

 - общий делитель
- общий делитель  и
и  .
.
2) пусть  - общий делитель
- общий делитель  и
и  .
.
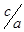 ,
, 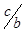

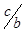

 (
( ,
,  ) =
) =  .
.
Лемма 2. Если  =
=  +
+ 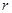 , то (
, то ( ,
,  ) = (
) = ( ,
, 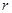 )
) 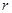
 0
0
Доказательство: пусть ( ,
,  ) =
) =  , тогда
, тогда
1) из  и
и 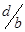 ,
, 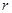 =
=  -
- 

2)  и
и 

 ,
,  - общий делитель
- общий делитель  и
и 




 = (
= ( ,
, 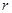 ).
).
( ,
,  ) = (
) = ( ,
, 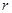 ).
).
Алгоритм Евклида
Пусть  и
и  - положительные числа,
- положительные числа,  >
>  >0. Разделим
>0. Разделим  на
на  , по теореме о делении с остатком:
, по теореме о делении с остатком:  =
= 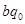 +
+ 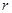 , 0
, 0  <
<  .
.
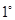 .
.  =0, т. е.
=0, т. е. 



 =
=  .
.
 .
. 
 0, то получаем ряд равенств:
0, то получаем ряд равенств:
 =
= 
 +
+  ; 0 <
; 0 <  <
<  (если
(если  =0, то процесс заканчивается).
=0, то процесс заканчивается).
 =
= 
 +
+  0<
0<  <
< 
- - - - - - - - - - - - - - - - - - - - - -
(I)  =
= 
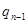 +
+  0<
0<  <
< 
 =
= 
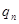
Процесс заканчивается, когда мы получаем 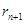 =0.
=0.
Последнее неизбежно, т. к. остатки, получаемые в процессе деления неотрицательны и убывают; следовательно, на каком-то шаге получим деление без остатка.
В силу леммы 2: ( ,
,  ) = (
) = ( ,
,  ) = (
) = ( ,
,  ) = …= (
) = …= ( ,
,  ) =
) =  .
.
Вывод: ( ,
,  ) двух чисел равен последнему неравному нулю остатку в процессе алгоритма Евклида.
) двух чисел равен последнему неравному нулю остатку в процессе алгоритма Евклида.
Пример. Найти (185, 55)= 5.
Задача отыскания НОД конечного множества чисел  ,...,
,...,  сводится к нахождению НОД для двух чисел.
сводится к нахождению НОД для двух чисел.
Теорема 1. Если ( ,
,  )=
)=  ; (
; ( ,
,  )=
)= 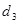 , …, (
, …, (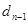 ,
,  )=
)=  , то
, то
( ,...,
,...,  )=
)=  . (Доказать самостоятельно).
. (Доказать самостоятельно).
Свойства НОД.
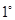 . Пусть
. Пусть  0,
0,  Z.
Z.
(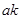 ,
,  )= (
)= ( ,
,  )
) 
Применим алгоритм Евклида 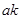 =
= 
 +
+ 

 =
= 

 +
+ 

- - - - - - - - - - - -

 =
= 

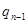 +
+ 


 =
= 

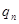
 (
(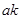 ,
,  )=
)= 
 = (
= ( ,
,  )
)  .
.
 . Пусть
. Пусть  - любой общий делитель
- любой общий делитель  и
и  , (
, ( ;
;  )=
)= 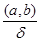
( ,
,  )= (
)= (
 ;
; 
 )= (
)= ( ;
;  )
) 
 св.2
св.2 
Свойства НОК
Определение 5. Целое число 
 0 называется ОК чисел
0 называется ОК чисел  ,...,
,...,  , если оно делится на
, если оно делится на  из данных чисел.
из данных чисел.
Среди совокупности ОК чисел особую роль играет одно число, называемое НОК.
Определение 6. Целое число  называется НОК чисел
называется НОК чисел  ,...,
,...,  , если
, если
1)  ОК(
ОК( ,...,
,...,  )
)
2)  ОК этих чисел
ОК этих чисел 
 , т.е.
, т.е. 
 …,
…, 

 (
( ).
).
Возникает вопрос о рациональном способе нахождения НОК. Один из практических способов – использование теоремы, которая устанавливает связь НОК и НОД.
Теорема. НОК двух чисел равно их произведение, деленное на НОД этих чисел.
 .
.
Доказательство: пусть  =ОК
=ОК 

 =
=  .
.
 – кратно и
– кратно и 
Пусть 


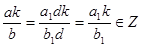 ,
, 
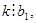 т. е.
т. е.  где
где 


 =
= 
НОК получим при 
 или
или 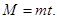
Вывод: совокупность общих кратных двух чисел совпадает с совокупностью кратных их общего наименьшего кратного.
Простые числа
Всякое целое число, больше 1, имеет не менее 2-х делителей, именно 1 и само себя.
Определение 1. Нaтуральное число p>1 называется простым, если p не имеет натуральных делителей, отличных от 1 и p.
Определение 2. Натуральное число a>1 называется составным, если a имеет, по крайней мере, один натуральный делитель, отличный от 1 и а.
1 не является ни простым, ни составным (т.к. имеет всего один натуральный делитель).
Первые простые числа в натуральном ряду: 2, 3, 5, 7, 11, 13, …
Простые числа – это элементы, при помощи, умножения которых строятся натуральные числа (>1); поэтому одной из важнейших задач теории чисел является изучение свойств простых чисел.
Свойства простых чисел:
1. p  n, n
n, n  N, n
N, n  1
1  p=n
p=n
Доказательство: пусть p  n
n  p имело бы 3 делителя 1, p, n, что невозможно, т.к. p- простое.
p имело бы 3 делителя 1, p, n, что невозможно, т.к. p- простое.
2. p1, p2 – различные простые числа  p2 не
p2 не  p1
p1
Доказательство: p2 – простое  p2 имеет делитель 1 и p2, но p2
p2 имеет делитель 1 и p2, но p2  p1
p1  p2
p2
не  p1
p1
3. n  N, p – простое
N, p – простое  n
n  p или (n, p)= 1
p или (n, p)= 1
Доказательство: пусть (p, n)= d 
 p- простое число
p- простое число  d= 1 или d = p, d = 1
d= 1 или d = p, d = 1  (d, n)
(d, n)  1; d = p
1; d = p  n
n  d, т.е. n
d, т.е. n  p
p
4. ab  p
p  a
a  p
p  b
b  p
p
Доказательство: если a  p – то утверждение теоремы справедливо, если a
p – то утверждение теоремы справедливо, если a
не  p
p  (a, p) = 1
(a, p) = 1  ab
ab  p
p  b
b  p
p
5. Если произведение нескольких сомножителей  p, то, по крайней мере, один из сомножителей
p, то, по крайней мере, один из сомножителей  p.(обобщение свойства 4)
p.(обобщение свойства 4) 
Теорема 1. Для  натурального числа a>1 наименьший отличный от единицы делитель есть число простое.
натурального числа a>1 наименьший отличный от единицы делитель есть число простое.
Доказательство: пусть q – наименьший  1 делитель натурального числа a>1; если бы q было составным, то оно имело бы некоторый делитель q1, с условием 1 < q1 < q, но a
1 делитель натурального числа a>1; если бы q было составным, то оно имело бы некоторый делитель q1, с условием 1 < q1 < q, но a  q и
q и 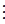 q
q  a
a  q1 , а это противоречит предположению относительно q.
q1 , а это противоречит предположению относительно q.
Date: 2016-11-17; view: 920; Нарушение авторских прав