Лекция №3 Отношение делимости в кольце Z. Сравнения в кольце Z. Теоремы Эйлера и Ферма.

Цель:

1.Рассмотрение отношения делимости в кольце Z.

2.Введение понятий НОД и НОК, связь между ними.

3.Формирование умений и навыков при решении практических задач.

План:

1. Отношение делимости, его простейшие свойства.

2. НОД. Алгоритм Евклида. НОК.

3. Простые числа.

Исторически теория чисел возникла как непосредственное развитие арифметики. В настоящее время в теорию чисел включают значительно более широкий круг вопросов, выходящих за рамки изучения натуральных чисел.

Современную теорию чисел можно в основном разбить на следующие разделы:

I. Элементарная теория чисел.

(теория сравнений; неопределенные уравнения; вопросы теории чисел, являющиеся непосредственным развитием теории делимости; вопросы о представимости чисел в определенной форме).

II. Алгебраическая теория чисел.

Изучаются различные классы алгебраических чисел.

III. Аналитическая теория чисел – те вопросы теории чисел, при изучении которых применяются методы математического анализа.

IV. Геометрическая теория чисел – проблемы, которые могут быть сформулированы в геометрической форме и к решению которых применяются геометрические соображения.

Мы будем изучать некоторые вопросы элементарной теории чисел.

Теория чисел занимается изучением свойств целых чисел .

1Отношение делимости, его простейшие свойства

Определение 1. Целое число а делится на целое число b, если существует такое целое число q, что a=b*q.

Число а называется делимым, b – делителем, q – частным.

Обратным к отношению является отношение «b делит а», которое обозначается b/а. отношение делимости (эта запись содержит в себе предположение, что ) является бинарным отношением в Z.

Свойства отношения делимости.

1⁰ Рефлексивность. имеем (так как а=а*1, 1 Z).

2⁰ Транзитивность.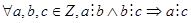

( ).

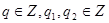3⁰ Любое число делится на 1: для (а=1*а).

4⁰ Если , то 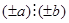, (то есть при любом сочетании знаков).

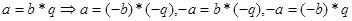, где .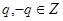

5⁰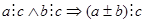

( )

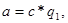
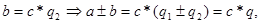
6⁰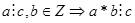

, где (в силу ассоциативности, коммутативности).

7⁰ (Следует из 5⁰, 6⁰) , .

8⁰ Если 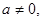то не существует такое 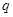, что 0* 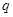=а.

(От противоположного: если бы существовало 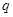от деления 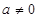на 0, то а= 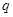*0, но 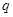*0=0 а=0, что противоречит условию). Коротко говоря, на нуль делить нельзя.

9⁰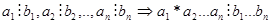

(, ).

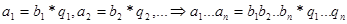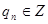10⁰ (Следствие 9⁰)

(частный случай, когда ).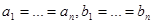

11⁰ , , потому что .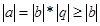

12⁰ (Следствие11⁰) либо

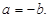
или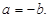

Date: 2016-11-17; view: 394; Нарушение авторских прав