Отношение сравнения, свойства сравнений

Пусть m – фиксированное натуральное число. Все целые числа по отношению к числу m разбиваются на m классов, если отнести к одному классу числа, дающие один и тот же остаток при делении на m. Числа, относящиеся к одному классу, называется сравнимыми, а теория, изучающая свойства классов, теорией сравнений.

Определение 1. Пусть m – натуральное число. Целые числа a и b называется сравнимыми по mod m, если их разность a – b 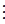m.

Запись a ≡ b (mod m). Читается «а сравнимо с b по mod m».

Сравнение представляет собой соотношение между 3 числами: a, b и m, причем m играет своего рода эталона сравнения – называется модулем.

Определение 2. Целые числа a и b называется сравнимыми по mod m, если остаток от деления этих чисел на m равны.

Предложение. Определения 1 – 2 равносильны.

Следствия.

1. a m ó a ≡ 0 (mod m)

Всякое число, кратное m, сравнимо с нулем по mod m.

2. a =mg + r ó a ≡ r (mod)

0 ≤ r < m

Всякое целое всегда сравнимо с остатком k, получающимся при делении его на m.

Свойства сравнений.

1⁰. рефлексивность: а ≡ а (mod m) а Є Z

a – a = 0 m

2⁰. симметричность: а ≡ b (mod m) => b ≡ а (mod m)

a – b m => b – a m

3⁰. транзитивность: а ≡ b (mod m) Λ b ≡ c (mod m) => a ≡ c (mod m)

a – b m Λ b – c m => (a – c) + (b – c) =a – c m

Вывод. Отношение сравнения на множестве Z по mod m является отношением эквивалентности => Z разбивается на непересекающийся между собой классы эквивалентности.

Эти классы – называются классами вычетов по модулю m или просто классами по mod m.

При этом числа из одного класса попарно сравнимы между собой, а числа из различных классов не сравнимы между собой => класс по mod m состоит из чисел, дающих один и тот же остаток при делении на m.

4⁰.Сравнения по одному и тому же модулю можно почленно складывать (вычитать)

а₁ ≡ b₁ (mod m)

а₂ ≡ b₂ (mod m)

______________

a₁ ± a₂ ≡ b₁ ± b₂ (mod m)

a₁ – b₁ m

=> (a₁ ± a₂) - (b₁ ± b₂) =(a₁ – b₁) ± (a₂ – b₂) m a₁ ± a₂ ≡ b₁ ± b₂(mod m)

a₂ – b₂ m

Следствия.

1.Любое слагаемое из одной части сравнения можно перенести в другую с противоположным знаком.

а + b ≡ с (mod m) => а ≡ с – b (mod m)

- b ≡ - b (mod m)

_______________

а ≡ с – b (mod m)

2. К любой части сравнения можно прибавить (отнять) число, кратное модулю.

а ≡ b (mod m) => а ≡ b – mk (… m)

0 ≡ mk (… m)

5⁰ Сравнения по одному и тому же mod можно почленно перемножить.

а₁ ≡ b₁ (mod m)

а₂ ≡ b₂ (… m)

_________________

a₁a₂ ≡ b₁b₂ (… m)

a₁a₂ – b₁b₂ = a₁a₂ – b₁b₂ + a₁b₂ – b₁b₂ = a₁ (a₂ – b₂) + b₂ (a₁ – b₁) m

Следствия.

1)Обе части сравнения можно умножить на одно и то же число

a ≡ b (… m) => ac ≡ bc (mod m) => a – b =mg => ac – bc ≡ m (gc)

2) Обе части сравнения можно вознести в одну и ту же натуральную степень.

a ≡ b (mod m) => aⁿ ≡ bⁿ (mod m)

6⁰ Обе части сравнения можно сократить на множитель, взаимно простой с модулем.

aс ≡ bс (mod m) Λ (c, m) = 1 => a ≡ b (mod m) => ac – bc m => c (a – b) m Λ (c, m) = 1 =>a – b m

7⁰ Обе части сравнения и модуль можно умножить на одно и то же число.

a ≡ b (mod m), r (mod m) Є Z => ak ≡ bk (mod mr)

a – b = mg => ak – bk = (mr)g k Є Z

8⁰ Если ak ≡ bk (mod mk) => a ≡ b (mod m) где r, m – произв. нат. ч.

Доказательство- самостоятельно.

9⁰ a ≡ b (mod m) Λ m d => a ≡ b (mod m) => a – b m и m d => a – b d

10⁰ a ≡ b (mod m) => множество общих делителей a и m совпадает с множеством общих делителей b и m. В частности, (a, m) = (b, m)

a – b m => a – b = mg и b = a – mg, т.е. общий делитель чисел а и m является общим делителем чисел b и m и наоборот.

Поскольку пара a и m и пара b и m имеют одни и те же общие делители, то и (a, m) = (b, m).

Другими словами: если одна часть сравнения и модуль делятся на какое – либо число, то и другая часть сравнения должна на то же число

a ≡ b (mod m)

11⁰ a ≡ b (mod m1)

a ≡ b (mod m2)

-------------------

a ≡ b (mod m_k) где m ≡ [m₁, …, m_k]

12⁰ Пусть f(x) – многочлен с целыми коэффициентами, a ≡ b (mod m) =>

f(a) ≡ f(b) (mod m)

Доказательство:

Пусть f(x) = c₀ xⁿ + c₁ x ^n-1 + … + c_n

a ≡ b (mod m) => a^k ≡ b^k (mod m) k = 0, …, n

Умножая обе части на c n-k

C _n-k a^k ≡ C _n-k b^k (mod m) k = 0, n

Складывая полученные сравнения, получим f(a) ≡ f(b) (mod m)