Автор знаменитых картин

(Явление Христа народу)

( Демон)

а) Репин б) Рублев в) Иванов г) Врубель

Задание 48

[Баженова]

По проекту архитектора (……….) был построен.

1) дом Пашкова в Москве

2) Московский университет

3) Зимний дворец в Петербурге

4)Собор Петропавловской крепости

Особенно легко и удобно создавать фасетные задания по естественному циклу дисциплин путем введения параметров в задания теста. Например, если нужно проверить умение решать квадратные уравнения, то, выбирая различные значения параметров — коэффициентов уравнения, можно получить множество вариантов фасета. Например, выбирая различные значения параметров а, Ь, с, обеспечивающие не отрицательность дискриминанта квадратного уравнения в задании,

Задание 49

Корни квадратного уравнения {а}х² + {b}х + {с} = О принадлежат интервалу

1)... 2)... 3)...

и добавляя соответствующие ответы, можно разработать множество заданий для различных вариантов теста.

При этом все ученики выполняют однотипные задания, но с различными коэффициентами, что отчасти устраняет возможность списывания, подсказки и других нарушений.

Одному ученику попадается уравнение х²+2х-3 = 0(а=1,b = = 2, с= -3), другому х² + 5х + 6 = 0 и т. д. Однако и здесь есть определенные осложнения, так как такого рода уравнения могут быть далеко не равноценными по трудности, поскольку гораздо удобнее делать вычисления при малых значениях коэффициентов, чем при больших. Поэтому говорить о полном устранении всех проблем разработки многовариантных тестов с помощью фасета, конечно, нельзя. Многие осложнения вполне преодолимы благодаря специальным методам, разрабатываемым для выравнивания результатов выполнения параллельных вариантов теста [47].

коррекция тестовых баллов с поправкой на догадку (задания с четырьмя и пятью ответами)

Формула коррекции на возможную догадку для индивидуальных баллов, полученных в результате выполнения заданий с четырьмя ответами, из которых один верный, имеет вид [43]

где все обозначения прежние.

Для рассмотренного ранее примера выполнения заданий с тремя ответами X_f= 50 и \V_t= 10. Скорректированный балл, полученный учеником при правильном выполнении 50 из 60 заданий теста с четырьмя ответами, будет

или округленно 47 баллов. Сопоставление с результатами коррекции для случая заданий с двумя и тремя ответами показывает, что испытуемому засчитывается 47 баллов из 50 правильных ответов, в то время как ранее засчитывалось 40 баллов (задание с двумя ответами) и 45 баллов (с тремя).

Для заданий с пятью ответами коррекция будет еще меньше. В этом случае

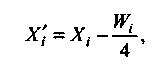
а для рассматриваемого примера

X_i^\= 50 –10/4= 50-2,5 = 48 баллов

48 баллов.

Таким образом, с увеличением количества дистракторов к заданию число вычитаемых баллов уменьшается, что вполне естественно, так как чем больше дистракторов, тем труднее угадать правильный ответ. Следовательно, в заданиях с большим количеством дистракторов на первый план при выборе правильного ответа выходят знания, а не догадка.

В целом же можно отметить, что формула коррекции индивидуальных баллов имеет довольно ограниченную сферу применения. Это связано с теми дополнительными трудностями, которые привносятся в процесс обработки скорректированных результатов тестирования, когда они после коррекции переносятся на область отрицательных и дробных чисел.

Действительно, если учащийся выполнил лишь незначительное количество заданий, то после коррекции его балл может стать отрицательным числом. Например, если X_i = 10, а всего в тесте 60 заданий с 5 ответами, то после коррекции

X'_i=10-50/4 = 10-12,5 = -2,5.

В этом случае приходится применять дополнительные преобразования скорректированных баллов, чтобы перевести их на область положительных целых чисел.

Правда, как уже отмечалось ранее, коррекция нужна не всегда. Если в инструкции для испытуемых содержалось требование не угадывать ответы к заданиям и переходить в случае затруднений к выполнению других заданий теста, то эффектом угадывания можно пренебречь. Хотя следует помнить, что далеко не все ученики при затруднениях поступят согласно требованиям инструкции, поэтому без коррекции результаты отдельных слабых учащихся будут явно завышены.

Date: 2016-11-17; view: 292; Нарушение авторских прав