Работа сил электростатического поля. Потенциал

Рассчитаем работу, совершаемую полем положительного точечного заряда q (рис. 34) по перемещению положительного пробного заряда q₀ из точки 1 в точку 2.

В процессе его движения сила взаимодействия

зарядов q и q₀ будет меняться. Сначала определим элементарную работу на малом участке пути dl, на котором эту силу можно считать постоянной:

,

где 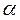– угол между перемещением и силой 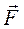. Учитывая, что 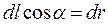, найдем полную работу суммированием элементарных работ на всем пути 1→2:

.

Отсюда видно, что работа кулоновских сил определяется только начальным и конечным положениями пробного заряда q₀ (не зависит от формы траектории). Это означает, что электростатическое поле является потенциальным, а кулоновские силы – консервативными.

Работа консервативных сил равна убыли потенциальной энергии:

.

Сопоставляя два последних выражения, получим формулу для потенциальной энергии заряда q₀, находящегося в поле заряда q:

.

Если принять в бесконечности W_p=0, то постоянная с будет равна нулю. Тогда

.

Отношение 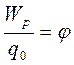не зависит от значения пробного заряда q₀ и является энергетической характеристикой поля, называемой потенциалом.

Потенциал – скалярная физическая величина, характеризующая способность поля совершать работу и измеряемая отношением потенциальной энергии пробного точечного заряда, помещенного в данную точку поля, к значению этого заряда. Можно также сказать, что потенциал данной точки поля равен работе, совершаемой полем при перемещении единичного положительного заряда из этой точки поля в бесконечность:

.

Потенциал поля точечного заряда q выражается формулой

.

Если заряд q перемещается из точки с потенциалом φ₁ в точку с потенциалом φ₂, то силы поля совершают работу

,

равную произведению заряда на разность потенциалов.

Знак потенциала определяется знаком заряда, создающего поле. Если поле образовано системой зарядов, то потенциал φ равен алгебраической сумме потенциалов полей, создаваемых каждым из зарядов в отдельности:

.

Точки пространства, в которых потенциал имеет одно и то же значение, образуют поверхность, называемую эквипотенциальной. Перемещение заряда вдоль этой поверхности не сопровождается работой (φ=const, dφ=0). Это означает, что силы электрического поля, а следовательно, и линии напряженности перпендикулярны к эквипотенциальным поверхностям.

За единицу потенциала принят вольт (В):

.

Потенциальные кривые на рисунке 35 выражают зависимость потенциальной энергии двух точечных зарядов от расстояния между ними (для одноименных зарядов W_p>0 и для разноименных W_p<0).

Так как обе потенциальные кривые не имеют минимума (потенциальной ямы), то система из двух неподвижных зарядов не может находиться в устойчивом равновесии: под действием кулоновских сил одноименные заряды расходятся на бесконечно большое расстояние, а разноименные – сближаются до слияния и нейтрализации. Это утверждение оказывается справедливым для любого числа зарядов при любом их расположении: всякая конфигурация покоящихся электрических зарядов неустойчива, если между ними действуют только кулоновские силы.

Это положение называется теоремой Ирншоу. Из нее, в частности, следует, что модель атома как система, состоящая из электрических зарядов, не может быть статической. Непрерывное движение электронов в атомах, колебания ядер в молекулах, ионов в кристаллах – необходимое условие устойчивости этих систем. Исследования показывают, что эти движения не прекращаются даже при абсолютном нуле температуры.

Таким образом, электрическое поле характеризуется двумя физическими величинами: напряженностью (силовая характеристика) и потенциалом (энергетическая характеристика); выясним как они связаны между собой. Пусть положительный заряд q перемещается силой электрического поля с эквипотенциальной поверхности, имеющей потенциал φ₀, на близко расположенную эквипотенциальную поверхность, имеющую потенциал φ_n< φ₀ (рис. 36).

Напряженность поля на всем малом пути Δx можно считать постоянной. Тогда работа перемещения

.

С другой стороны,

.

Сопоставляя две последних формулы, получим

;

знак минус обусловлен тем, что напряженность поля направлена в сторону убывания потенциала, тогда как градиент потенциала направлен в сторону возрастания потенциала.

Итак, напряженность поля равна по величине и противоположна по направлению градиенту потенциала. Это показывает, что единицей измерения напряженности электрического поля является 1 В/м.

Date: 2016-11-17; view: 589; Нарушение авторских прав