Предварительные теоретические сведения

Общие положения и определения.

В электрической цепи при параллельном соединении элементов (рис. 69) ток в неразветвленной части цепи определяется по формуле:

I=U 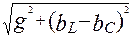=Ug,

где: g= I/R - активная проводимости параллельных ветвей;

b_L= I/X_{L -} - реактивная индуктивная проводимости параллельных ветвей;

b_C = I/X_C - реактивная ёмкостная проводимости параллельных ветвей.

Рисунок 69. Параллельное соединении активного, индуктивного и емкостного сопротивлений в режиме резонанса токов

Особый интерес представляет случай, когда индуктивная (b_L) и емкостная (b_С) реактивные проводимости равны друг другу по величине:

b_L=b_C.

Это равенство называется условием резонанса токов. В этом случае полная проводимость цепи:

y= 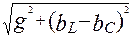= g,

а полный ток I = Ug имеет минимальное значение и только активную составляющую тока:

I = I_а = Ug.

Следовательно: cosφ =1.

Токи в ветвях с емкостью и индуктивностью соответственно равны:

I_L = Ub_L = I(); I_C= Ub_C = I(),

т.е. равны по величине (I_L = I_C) и могут превышать полный ток в цепи в раз, если b_L = b_C>g. Векторная диаграмма токов для рассмотренного случая представлена на рис. 70.

Рисунок 70. Векторная топографическая диаграмма токов и напряжения при параллельном соединении элементов цепи для случая резонанса токов

Векторная диаграмма построена согласно уравнению:

_.

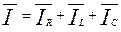Из векторной диаграммы следует, что реактивные токи I_C и I_L компенсируют друг друга, и из сети будет потребляться только активная мощность:

S = Р = .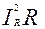

Режим работы электрической цепи при параллельном соединении элементов R, L, С, когда b_L=b_С,а токи в ветвях с реактивными проводимостями равны по величине, называется резонанс ом токов. Для этого режима характерны следующие соотношения:

I = I_R,

cosφ = 1,

φ = 0,

Р = UI cosφ = UI = S,

Q_L = U²b_L, Q_C = U²b_C, Q = Q_L - Q_C = 0.

В режиме резонанса токов, хотя из сети и не потребляется реактивная мощность, через каждую четверть периода происходит обмен энергией между магнитным полем индуктивности и электрическим полем емкости, который поддерживается напряжением источника питания.

В частном случае, когда активная проводимость g = 0, полный ток

I = Ug = 0.

Тогда в замкнутом LC -контуре протекает ток I_L = I_C > 0, т.к. реальные индуктивные катушки и конденсаторы обладают активным сопротивлением. Схему для такого случая при параллельном соединении L и С можно представить как на рис. 71:

Рисунок 71. Параллельное соединение реальных индуктивного и емкостного элементов цепи в режиме резонанса токов

Резонанс токов в такой цепи имеет место, если b₁=b_{2 ,}

где: b₁₌ - реактивная индуктивная проводимость первой ветви;

b₂ = - реактивная емкостная проводимость второй ветви.

Ток в неразветвленной части цепи согласно перв ом у закону Кирхгофа будет равен:

_.

Согласно данному уравнению построена векторная диаграмма рис 72:

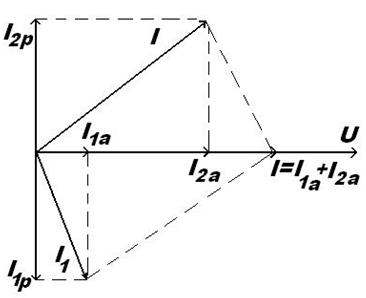
Рисунок 72. Векторная топографическая диаграмма токов и напряжения при параллельном соединении реальных индуктивного и емкостного элементов цепи для случая резонанса токов

Так как при резонансе токов b₁ = b₂, то реактивные составляющие токов I₁ и I₂ равны по величине и противоположны по направлению.

Поэтому: = .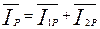

Таким образом, полный ток имеет только активную составляющую, как и при резонансе токов в цепи с идеальными катушкой индуктивности и конденсатором: =

В этом режиме цепь также не будет потреблять из сети реактивную мощность: Q = Q_L - Q_C = 0.

Date: 2016-11-17; view: 425; Нарушение авторских прав