
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Предварительные теоретические сведения
|
|
Общие положения и определения.
В электрической цепи (рис. 62) при последовательном соединении элементов идут процессы и явления аналогичные происходящим в контуре, состоящем из последовательно соединенных катушки и конденсатора переменной емкости, включенных в цепь внешней синусоидальной ЭДС технической частоты 50 Гц.

Рисунок 62. Последовательное соединении активного, индуктивного и емкостного сопротивлений в режиме резонанса напряжений
По отношению к источнику ЭДС элементы цепи включены последовательно. В такой цепи при определенных значениях R, L и С ток определяется по известному закону Ом а:
I= 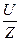 .
.
По модулю полное сопротивление:
Z=  ,
,
где: (XL-XC) - реактивное сопротивление контура;
XL=ωL - индуктивное сопротивление катушки индуктивности;
XC =  - емкостное сопротивление конденсатора;
- емкостное сопротивление конденсатора;
 - циклическая частота используемого синусоидального тока.
- циклическая частота используемого синусоидального тока.
Условие электрического равновесия такой цепи определяется вторым закон ом Кирхгофа:
U= UR+UL+UC.
Соответственно для синусоидального тока:
I=Im sinn ωt
Напряжения на элементах цепи соответственно будут равны:
U=UmR sinn ωt;
UL=UmL sinn (ωt+  );
);
Uc=UmC sinn (ωt-  ).
).
Фазовые соотношения между током и напряжениями можно определить с помощью векторных диаграмм рисунков 63, 64, 65.

Рисунок 63. Векторная топографическая диаграмма тока и напряжений при последовательном соединения элементов цепи для случая UL > UС

Рисунок 64. Векторная топографическая диаграмма тока и напряжений при последовательном соединения элементов цепи для случая UL < UС

Рисунок 65. Векторная топографическая диаграмма тока и напряжений при последовательном соединения элементов цепи для случая UL = UС
На векторных диаграммах получен треугольник напряжений, гипотенуза которого равна приложенному напряжению U. При этом разность фаз φопределяет характер нагрузки в цепи:
· при UL > UС угол φ > 0 - индуктивный характер нагрузки (рис. 63); XL-Хс > 0;
· при UC > UL угол φ < 0 - емкостный характер нагрузки (рис. 64); XL - XC .< 0 и XC>XL;
· при UC=UL угол φ = 0 –нагрузка чисто активная (рис. 65); XL — ХC = 0. и XL = XC . В цепи в этом случае протекает максимальный ток:
I= 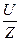 =
=  , Z=R.
, Z=R.
Следовательно, в данном случае ток и напряжение совпадают по фазе. Явление, при котором в электрической цепи синусоидального тока при последовательном соединении активного, индуктивного и емкостного сопротивлений, когда XL = XC,а общее напряжение совпадает по фазе с током цепи, называется резонанс ом напряжений (рис. 65).
Условием резонанса напряжений является равенство индуктивного и ёмкостного сопротивлений цепи:
XL = XC, ώL=  .
.
В режиме резонанса напряжений справедливы равенства:
 ,
,  ,
,
где: 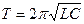 - формула Томсона для колебательного контура.
- формула Томсона для колебательного контура.
Итак, для резонанса напряжений в электрической цепи можно записать следующие выражения:
I= 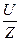 =
=  ;
;
XL = XC, φ=0;
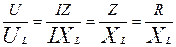 ;
;
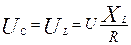 , так как UL=XLI, UC=XCI.
, так как UL=XLI, UC=XCI.
В реальных цепях может быть режим, при котором XL>R. Соответственно, напряжение UL и равное ему UC окажутся больше приложенного напряжение в  раз, т.е. на отдельных участках цепи могут возникать при резонансе напряжения, опасные для обмоток приборов и машин, включённых в данную цепь. Это условие необходимо учитывать при расчётах силовых цепей. В радиотехнических колебательных контурах явление резонанса напряжений используется для усиления слабых радиосигналов. За счёт того, что
раз, т.е. на отдельных участках цепи могут возникать при резонансе напряжения, опасные для обмоток приборов и машин, включённых в данную цепь. Это условие необходимо учитывать при расчётах силовых цепей. В радиотехнических колебательных контурах явление резонанса напряжений используется для усиления слабых радиосигналов. За счёт того, что
XL>>R, UL=U 
сигнал усиливается в  раз.
раз.
Из условия φ= 0, cosφ= 1 при резонансе напряжений можно  определить энергетические соотношения и мощность цепи. Активная мощность такой цепи:
определить энергетические соотношения и мощность цепи. Активная мощность такой цепи:
Р= IUcosφ = IU = S.
Активная мощность равна полной мощности.
Реактивная мощность:
QL=XLI2 QC = XCI2; Q= QL-QC=0.
Т.е. реактивные части реактивной мощности при резонансе напряжений находятся в противофазе. Физический смысл этого явления следующий: через каждую четверть периода происходит обмен энергией между магнитным полем катушки и электрическим полем конденсатора. Равенства емкостного и индуктивного сопротивлений:
ω L= 
можно добиться, изменяя угловую частоту ω, индуктивность L, ( например меняя положение сердечника катушки) или емкость конденсатора С. Угловая частота, при которой наступает резонанс напряжений:

называется резонансной частотой. При резонансной частоте ток в цепи максимален:
I=  ,
,
т. е. цепь в этом случае имеет наименьшее возможное сопротивление R, а напряжения на индуктивности и емкости UL и UC сдвинутые по фазе на π, полностью компенсируют друг друга. Напряжение, приложенное к цепи, равно напряжению на активном сопротивлении, и ток совпадает по фазе с напряжением.
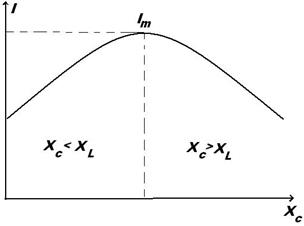
Если в цепь с постоянной индуктивностью включить последовательно переменную емкость и постепенно ее изменять (увеличивать), то ток в цепи будет сначала расти до наступления резонанса, а затем убывать (рис 66)
| 
|
| Рисунок 66. Зависимость тока в цепи I от ёмкостного сопротивления XC | Рисунок 67. Изменение тока в цепи и коэффициента мощности методом последовательной компенсации |
Уменьшение реактивного сопротивления цепи за счет введения в цепь электрической ёмкости называют последовательной к ом пенсацией:
· при Хс < XL получается недокомпенсация (см. рис. 67);
· при XC> XL - перекомпенсация;
· при ХС = XL -полная компенсация. Ток в цепи максимален, и cosφ =1.
Этим способом компенсации на практике пользуются для повышения коэффициента мощности cosφ в сетях.
Date: 2016-11-17; view: 419; Нарушение авторских прав