
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Как использовать статистику
|
|
Существует резкое различие между
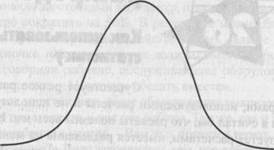
менеджерами, использующими расчеты и не использующими таковые, хотя я считал бы, что расчеты полезны всем им. Но и среди тех, кто пользуется расчетами, имеется разделение на менеджеров, осведомленных в статистике, и тех, кто не осведомлены. Требования повышения качества, обычно включающие SPC (Контроль статистической обработки), повышают осведомленность в области статистики, но обычно только среди специалистов-производственников. И это очень жаль, потому что статистика может быть полезна для всех1. Одной из наиболее полезных концепций статистики является нормальное распределение, как показано на рис. 26.1, который характеризует рост мужчин в Соединенном Королевстве (UK).
Средний рост мужчин в UK (т.е. сумма величин роста всех мужчин, деленная на количество мужчин), вероятно, составляет около 5 футов 9 дюймов (175 см). Мода роста (наиболее распространенный рост) примерно такая же. Медиана роста (такой рост, по отношению к которому мужчин меньшего роста столько же, сколько большего), вероятно, тоже близка к этой величине.
Если мы изобразим графически численность мужчин разного роста (в футах и дюймах, либо в метрах) в процентах от всего населения, то получим похожую на колокол кривую, представляющую нормальное распределение. Эта кривая симметрична относительно средней точки. Другими словами, количество мужчин ростом 5 футов 8 дюймов и ростом 5 футов 10 дюймов одинаково. Аналогично имеется столько же мужчин (но намного меньше, чем в предыдущем случае) ростом 5 футов и 6 дюймов, сколько ростом 6 футов. Опять-таки количество мужчин (теперь намного меньшее) ростом 5 футов 3 дюйма равно числу мужчин ростом 6 футов 3 дюйма. И наконец, будет очень мало, но тем не менее будет, мужчин ростом 5 футов и ниже, причем их число будет равно числу мужчин ростом 6 футов 6 дюймов и выше.
8-339

| Рост |
Численность
 5'0" 5'3" 5'6" 5'8" 5'9"5'10"6'0" 6'3" 6'6"
5'0" 5'3" 5'6" 5'8" 5'9"5'10"6'0" 6'3" 6'6"
Рис. 26.1. Нормальное распределение
Конечно, эта кривая, как и все модели в этой книге, идеализирована. Но как и другие модели, она реалистична. Многие показатели имеют нормальное распределение, например, уровень интеллекта (IQ), для которого величина 100 составляет среднее, медиану и моду. Поэтому людей с IQ, равным 85 и меньше, столько же, сколько с IQ, равным 115 и выше.
Какую практическую пользу дает нормальное распределение? Оно предоставляет нам гигантские возможности для предвидения.
Date: 2016-11-17; view: 303; Нарушение авторских прав