Свободные и вынужденные колебания

При совпадении частоты вынужденных колебаний с частотой свободных колебаний системы наступает резонанс. Гармонические свободные и вынужденные колебания характеризуют амплитудой, периодом и фазой.

Многие процессы вокруг нас повторяются во времени. Так, звук электрического звонка представляет собой периодически повторяющиеся изменения давления воздуха. При этом ток в электрической цепи звонка тоже периодически изменяется или, как говорят, является переменным. Периодические изменения любых физических величин называют колебаниями.

Примером колебаний могут служить колебания положения груза, подвешенного на пружине. Если вывести груз из положения равновесия, оттянув его вниз и отпустить, то груз начнёт совершать колебательные движения – вверх-вниз, вверх-вниз и т.д. Если пренебречь силой трения о воздух, действующей на груз, то систему «пружина-груз-Земля» или пружинный маятник можно считать замкнутой. Колебания физических величин, возникающие в замкнутых системах под действием внутренних сил, называют свободными колебаниями.

Рассмотрим причины возникновения свободных колебаний на примере пружинного маятника. При отклонении груза вниз на расстояние А от положения равновесия сила упругости пружины возрастает, и когда груз отпускают, он начинает двигаться с ускорением вверх к положению равновесия и скорость его растёт. Через некоторое время груз достигает положения равновесия и в этот момент сумма сил, действующих на груз, становится равной нулю, а скорость его – максимальной v _max. Затем груз по инерции проходит положение равновесия и отклоняется в противоположную сторону, в результате чего пружина укорачивается, и результирующая сил, приложенных к грузу, начинает действовать вниз, тормозя его движение. В самом верхнем положении скорость груза уменьшается до нуля, а потом под действием результирующей силы он опять начинает двигаться к положению равновесия, увеличивая свою скорость. Но при достижении точки равновесия груз приобретает максимальную скорость и опять проскакивает точку равновесия. Потом груз постепенно тормозится до полной остановки в крайнем нижнем положении, и всё повторяется сначала.

Сила, стремящаяся возвратить систему в положение равновесия, является необходимым условием появления свободных колебаний в пружинном маятнике и других колебательных системах. Отметим, что в крайних положениях пружинного маятника система обладает только потенциальной энергией деформированной пружины. Наоборот, когда груз проходит через положение равновесия, система обладает только кинетической энергией.

Колебания, вызванные внешними периодически изменяющимися силами, называют вынужденными колебаниями. Например, можно вызвать вынужденные колебания у обычных подвесных качелей, если периодически толкать их в разные стороны. Из опыта известно, что вынужденные колебания достигают наибольшей амплитуды, когда их частота совпадает с частотой свободных колебаний системы. Такое резкое возрастание амплитуды вынужденных колебаний называют резонансом.

Периодические изменения физических величин, происходящие по закону синуса или косинуса, называются гармоническими колебаниями. Так, например, изменения положения x и вертикальной скорости v пружинного маятника со временем t можно описать следующим образом:

x =- A ^.cos(w t) (98)

v = v _max^.sin(w t), (99)

где A и v _max^. – амплитуды соответствующих колебаний, а w - их циклическая или круговая частота, которая следующим образом связана с обычной частотой n и периодом колебаний Т:

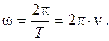(100)

Величину, от которой берут синус или косинус в (98, 99) называют фазой колебаний, j. Как следует из (98, 99), фаза колебаний определяет состояние системы.

Date: 2016-08-31; view: 408; Нарушение авторских прав