Второе начало термодинамики. Энтропия

1.8.1. Водород совершает цикл Карно. Найти КПД цикла, если при адиабатическом расширении:

а) объем газа увеличивается в n = 2,0 раза;

б) давление уменьшается в n = 2,0 раза.

1.8.2. Идеальный газ совершает цикл, состоящий из чередующихся изотерм и адиабат. Температуры, при которых происходят изотермические процессы, равны T ₁, T ₂ и T ₃. Найти КПД такого цикла, если при каждом изотермическом расширении объем газа увеличивается в одно и то же число раз.

1.8.3. Найти КПД цикла, состоящего из двух изохор и двух адиабат, если в пределах цикла объем идеального газа изменяется в n = 10 раз. Рабочим веществом является азот.

1.8.4. Найти КПД цикла, состоящего из двух изобар и двух адиабат, если в пределах цикла давление изменяется в n раз. Рабочее вещество – идеальный газ с показателем адиабаты γ.

1.8.5. Идеальный газ совершает цикл, состоящий из:

а) изохоры, адиабаты и изотермы;

б) изобары, адиабаты и изотермы,

причем изотермический процесс происходит при минимальной температуре цикла. Найти КПД каждого цикла, если температура T в его пределах изменяется в n раз.

1.8.6. Идеальный газ совершает цикл, состоящий из:

а) изохоры, адиабаты и изотермы;

б) изобары, адиабаты и изотермы,

причем изотермический процесс происходит при максимальной температуре цикла. Найти КПД каждого цикла, если температура T в его пределах изменяется в n раз.

1.8.7. Идеальный газ с показателем адиабаты γ совершает прямой цикл, состоящий из адиабаты, изобары и изохоры. Найти КПД цикла, если при адиабатическом процессе объем идеального газа:

а) увеличивается в n раз; б) уменьшается в n раз.

1.8.8. Найти (в расчете на моль) приращение энтропии углекислого газа при увеличении его температуры T в n = 2,0 раза, если процесс нагревания:

а) изохорический; б) изобарический.

Газ считать идеальным.

1.8.9. Во сколько раз следует увеличить изотермически объем идеального газа в количестве ν = 4,0 моль, чтобы его энтропия испытала приращение ?

1.8.10. Два моля идеального газа сначала изохорически охладили, а затем изобарически расширили так, что температура газа стала равной первоначальной. Найти приращение энтропии газа, если его давление в данном процессе изменилось в n = 3,3 раза.

1.8.11. Найти приращение энтропии двух молей идеального газа с показателем адиабаты γ = 1,30, если в результате некоторого процесса объем газа увеличился в = 2,0 раза, а давление уменьшилось в = 3,0 раза.

1.8.12. Один моль идеального газа с показателем адиабаты γ совершает политропический процесс, в результате которого температура газа увеличивается в τ раз. Показатель политропы n. Найти приращение энтропии газа в данном процессе.

1.8.13. Процесс расширения двух молей аргона происходит так, что давление газа увеличивается прямо пропорционально его объему. Найти приращение энтропии газа при увеличении его объема в = 2,0 раза.

1.8.14. Идеальный газ с показателем адиабаты у совершает процесс по закону , где и – положительные постоянные, V - объем. При каком значении объема энтропия газа окажется максимальной?

1.8.15. Один моль идеального газа совершает процесс, при котором энтропия газа изменяется с температурой T по закону , где a – положительная постоянная, – молярная теплоемкость данного газа при постоянном объеме. Найти, как зависит температура газа от его объема в этом процессе, если при .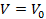

1.8.16. Один моль идеального газа с известным значением теплоемкости C _V совершает процесс, при котором его энтропия S зависит от температуры T как , где – постоянная. Температура газа изменилась от T ₁ до T ₂. Найти:

a) молярную теплоемкость газа как функцию T;

б) количество теплоты, сообщенной газу;

в) работу, которую совершил газ.

1.8.17. Рабочее вещество совершает цикл, в пределах которого температура T изменяется в n раз, а сам цикл имеет вид, показанный:

а) на рис. а; б) на рис. б,

где S — энтропия. Найти КПД цикла.

1.8.18. Теплоизолированный цилиндр разделен невесомым поршнем на две одинаковые части. По одну сторону поршня находится один моль идеального газа с показателем адиабаты γ, а по другую сторону – вакуум. Начальная температура газа T ₀. Поршень отпустили, и газ заполнил весь цилиндр. Затем поршень медленно переместили в начальное положение. Найти приращение внутренней энергии и энтропии газа в результате обоих процессов.

1.8.19. Теплоизолированный сосуд разделен перегородкой на две части так, что объем одной из них в n = 2,0 раза больше объема другой. В меньшей части находится моль азота, а в большей части моль кислорода. Температура газов одинакова. В перегородке открыли отверстие, и газы перемешались. Найти приращение энтропии системы, считая газы идеальными.

1.8.20. Два одинаковых теплоизолированных сосуда, соединенные трубкой с. вентилем, содержат по одному молю одного и того же идеального газа. Температура газа в одном сосуде T ₁ в другом T ₂. Молярная теплоемкость газа C _V известна. После открывания вентиля газ пришел в новое состояние равновесия. Найти 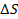– приращение энтропии газа. Показать, что .

Date: 2016-06-06; view: 2900; Нарушение авторских прав