Законы сохранения импульса, энергии и момента импульса

1.3.1. Система состоит из двух шариков масс m ₁ и m ₂, которые соединены между собой пружинкой. В момент t = 0 шарикам сообщили скорости и , после чего система начала двигаться в однородном поле тяжести Земли. Найти зависимости от времени импульса этой системы в процессе движения и радиус-вектора ее центра масс относительно его начального положения.

1.3.2. Через блок перекинута веревка, на одном конце которой висит лестница с человеком, а на другом – уравновешивающий груз массы M. Человек массы m совершил перемещение l’ относительно лестницы вверх и остановился. Пренебрегая массами блока и веревки, а также трением в оси блока, найти перемещение l центра масс этой системы.

1.3.3. Цепочка массы m = 1,00 кг и длины l = 1,40 м висит на нити, касаясь поверхности стола своим нижним концом. После пережигания нити цепочка упала на стол. Найти полный импульс, который она передала столу.

1.3.4. Две одинаковые тележки движутся друг за другом по инерции (без трения) с одной и той же скоростью . На задней тележке находится человек массы m. В некоторый момент человек прыгнул в переднюю тележку со скоростью u относительно своей тележки. Имея в виду, что масса каждой тележки равна M, найти скорости, с которыми будут двигаться обе тележки после этого.

1.3.5. Ракета начала подниматься вертикально вверх в однородном поле сил тяжести. Начальная масса ракеты (с топливом) равна m ₀. Скорость газовой струи относительно ракеты равна u. Найти скорость ракеты в зависимости от ее массы m и времени подъема t.

1.3.6. Цепочка AB длины l находится в гладкой горизонтальной трубке так, что часть ее длины l свободно свешивается, касаясь своим концом B поверхности стола. В некоторый момент конец A цепочки отпустили. С какой скоростью он выскочит из трубки?

1.3.7. Частицы массы m попадают в область, где на них действует встречная тормозящая сила. Глубина x проникновения частиц в эту область зависит от импульса p частиц как , где — заданная постоянная. Найти зависимость модуля тормозящей силы от x.

1.3.8. Два бруска массами m ₁ и m ₂, соединенные недеформированной пружинкой, лежат на горизонтальной плоскости. Коэффициент трения между брусками и плоскостью равен k. Какую минимальную постоянную силу нужно приложить в горизонтальном направлении к бруску с массой m ₁, чтобы другой брусок сдвинулся с места?

1.3.9. Частица массы m движется по окружности радиуса R с нормальным ускорением, которое меняется со временем по закону 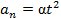, где - постоянная. Найти зависимость от времени мощности всех сил, действующих на частицу, а также среднее значение этой мощности за первые t секунд после начала движения.

1.3.10. Небольшому телу массы m, находящемуся на горизонтальной плоскости, сообщили скорость . Коэффициент трения зависит от пройденного пути s по закону k = , где — постоянная. Найти максимальную мгновенную мощность силы трения.

1.3.11. Тело массы m начинают поднимать с поверхности Земли, приложив к нему силу F, которую изменяют с высотой подъема y по закону F = 2 ( - 1) m g, где - положительная постоянная. Найти работу этой силы и приращение потенциальной энергии тела в поле тяжести Земли на первой половине пути подъема.

1.3.12. Частица массы m движется со скоростью под углом к нормали плоскости, разделяющей области, в которых потенциальная энергия частицы равна U _l и U ₂. Под каким углом к нормали она будет двигаться после пересечения этой плоскости? При каком условии частица не проникнет во вторую область?

1.3.13. В K -системе отсчета вдоль оси x движутся две частицы: одна массы m ₁ – со скоростью v ₁, а другая массы m ₂ – со скоростью v ₂. Найти:

а) скорость V K’ -системы отсчета, в которой суммарная кинетическая энергия этих частиц минимальна;

б) суммарную кинетическую энергию этих частиц в K’ -системе.

1.3.14. Частица A массы m, пролетев вблизи другой покоившейся частицы B, отклонилась на угол α. Импульс частицы A до взаимодействия был равен p ₀, после взаимодействия стал p. Найти массу частицы B, если система замкнутая.

1.3.15. Замкнутая система состоит из двух одинаковых частиц, которые движутся со скоростями и так, что угол между направлениями их движения равен . После упругого столкновения скорости частиц оказались равными и . Найти угол между направлениями их разлета.

1.3.16. Замкнутая система состоит из двух частиц с массами m ₁ и m ₂, движущихся под прямым углом друг к другу со скоростями и . Найти в системе их центра масс:

а) импульс каждой частицы;

б) суммарную кинетическую энергию обеих частиц.

1.3.17. Момент импульса частицы относительно точки O меняется со временем по закону M = a + b t ², где a и b — постоянные векторы, причем a b. Найти относительно точки O момент N силы, действующей на частицу, когда угол между векторами N и M окажется равным 45°.

1.3.18. Частица движется по замкнутой траектории в центральном силовом поле, где ее потенциальная энергия U = kr ², k — положительная постоянная, r - расстояние частицы до центра поля O. Найти массу частицы, если наименьшее расстояние ее до точки O равно r ₁, а скорость на наибольшем расстоянии от этой точки — .

1.3.19. На гладкой горизонтальной плоскости движется небольшое тело массы m, привязанное к нерастяжимой нити, другой конец которой втягивают в отверстие O с постоянной скоростью. Найти силу натяжения нити в зависимости от расстояния r тела до отверстия, если при r = r ₀ угловая скорость нити была равна ω₀.

1.3.20. Система частиц имеет суммарный импульс p и момент импульса M относительно точки O. Найти ее момент импульса M’ относительно точки O’, положение которой по отношению к точке O определяется радиус-вектором r ₀. В каком случае момент импульса системы частиц не будет зависеть от выбора точки O?

Date: 2016-06-06; view: 2800; Нарушение авторских прав