Механические колебания

1.6.1. Найти круговую частоту и амплитуду гармонических колебаний частицы, если на расстояниях x ₁ и x ₂ от положения равновесия ее скорость равна и .

1.6.2. Найти графически амплитуду A колебаний, которые возникают при сложении следующих колебаний:

а) ,

б) , , .

1.6.3. Точка движется в плоскости xy по закону 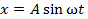, , где A, B, — постоянные. Найти:

а) уравнение траектории точки y (x) и направление ее движения по этой траектории;

б) ускорение a точки в зависимости от ее радиус-вектора r относительно начала координат.

1.6.4. Частица массы m находится в одномерном силовом поле, где ее потенциальная энергия зависит от координаты x как , и — постоянные. Найти период малых колебаний частицы около положения равновесия.

1.6.5. Частица массы m находится в одномерном силовом поле, где ее потенциальная энергия зависит от координаты x как , и — постоянные. Найти период малых колебаний частицы около положения равновесия.

1.6.6. Идеальная жидкость объема V = 16 см³ налита в изогнутую трубку с площадью сечения канала S = 0,50 см². Найти период малых колебаний жидкости.

1.6.7. Вычислить период малых колебаний ареометра, которому сообщили небольшой толчок в вертикальном направлении. Масса ареометра m = 50 г, радиус его трубки r = 3,2 мм, плотность жидкости ρ = 1,00 г/см³. Сопротивление жидкости пренебрежимо мало.

1.6.8. Однородный стержень положили на два быстро вращающихся блока, как показано на рисунке. Расстояние между осями блоков l = 20 см, коэффициент трения между стержнем и блоками k = 0,18. Показать, что стержень будет совершать гармонические колебания. Найти их период.

1.6.9. Небольшой брусок начинает скользить по наклонной плоскости, составляющей угол с горизонтом. Коэффициент трения зависит от пройденного пути s по закону k = as, где a – постоянная. Найти время движения бруска.

1.6.10. Тело A массы m ₁ = 1,00 кг и тело B массы m ₂ = 4,10 кг соединены между собой легкой пружиной. Тело A совершает свободные вертикальные гармонические колебания с амплитудой a = 1,6 см и частотой . Найти наибольшее и наименьшее значения силы давления этой системы на опорную плоскость.

1.6.11. Доска, на которой лежит тело массы m, начинает двигаться вертикально вверх по закону , где y – смещение из начального положения, . Найти:

а) минимальную амплитуду колебания доски, при которой тело начнет отставать от нее;

б) амплитуду колебания доски, при которой тело подскочит на высоту h =50 см относительно начального положения (в момент t = 0).

1.6.12. Частица массы m движется под действием силы , где — положительная постоянная, - радиус-вектор частицы относительно начала координат. Найти траекторию ее движения, если в начальный момент r = r ₀ i и скорость v = v ₀ j, где i и j — орты осей x и y.

1.6.13. Тело массы m упало с высоты h на чашку пружинных весов. Массы чашки и пружины пренебрежимо малы, жесткость последней . Прилипнув к чашке, тело начинает совершать гармонические колебания в вертикальном направлении. Найти амплитуду колебаний и их энергию.

1.6.14. Тело массы m упало с высоты h на чашку пружинных весов. Массы чашки M, масса пружины пренебрежимо малы, жесткость последней . Прилипнув к чашке, тело начинает совершать гармонические колебания в вертикальном направлении. Найти амплитуду колебаний и их энергию.

1.6.15. Частица массы m движется в плоскости xy под действием силы, зависящей от скорости по закону , где a — положительная постоянная, i и j — орты осей x и y. В начальный момент t = 0 частица находилась в точке и имела скорость в направлении орта j. Найти закон движения частицы x (t), y (t), а также уравнение ее траектории.

1.6.16. Найти круговую частоту малых колебаний тонкого однородного стержня массы m и длины l вокруг горизонтальной оси, проходящей через точку O. Жесткость пружины . В положении равновесия стержень вертикален.

1.6.17. Однородный стержень массы m совершает малые колебаний вокруг горизонтальной оси, проходящей через точку O. Правый конец стрежня подвешен на пружине жесткости . Найти период колебаний стержня, если в положении равновесия он горизонтален.

1.6.18. Однородный стержень массы m =1,5 кг, висящий на двух одинаковых нитях длины l = 90 см, повернули на малый угол вокруг вертикальной оси, проходящей через его середину C. При этом нити отклонились на угол = 5,0°. Затем стержень отпустили. Найти:

а) период колебаний;

б) энергию колебаний стержня.

1.6.19. Горизонтальный однородный диск массы m и радиуса R укреплен на конце тонкого стержня AO. При повороте диска на угол вокруг оси AO на него действует момент упругих сил , где постоянная. Найти амплитуду малых крутильных колебаний и их энергию, если в начальный момент диск отклонили на угол ₀ и сообщили ему угловую скорость .

1.6.20. Найти частоту малых колебаний системы, показанной на рисунке. Известны радиус блока R, его момент инерции I относительно оси вращения, масса тела m и жесткость пружины . Массы нити и пружины пренебрежимо малы, нить по блоку не скользит, трения в оси блока нет.

Date: 2016-06-06; view: 2532; Нарушение авторских прав