Динамика твердого тела

1.4.1. Однородный шар массы m = 4,0 кг движется поступательно по поверхности стола под действием постоянной силы F, как показано на рисунке. Угол α = 45°, коэффициент трения k = 0,20. Найти F и ускорение шара.

1.4.2. Тонкая однородная пластинка массы m = 0,60 кг имеет форму равнобедренного прямоугольного треугольника. Найти ее момент инерции относительно оси, совпадающей с одним из катетов, длина которого a = 200 мм.

1.4.3. Вычислить моменты инерции однородного сплошного конуса относительно его оси симметрии и оси, перпендикулярной оси симметрии, проходящей через вершину конуса, если масса конуса т, радиус основания R и высота конуса H.

1.4.4. Концы тонких нитей, плотно намотанных на ось радиуса r диска Максвелла, прикреплены к горизонтальной штанге. Когда диск раскручивается, штангу поднимают так, что диск остается неизменно на одной и той же высоте. Масса диска с осью m, их момент инерции относительно их оси симметрии I. Найти ускорение штанги.

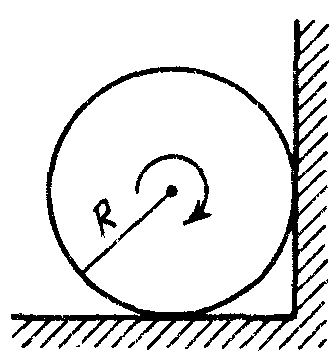1.4.5. Однородный сплошной цилиндр радиуса R раскрутили вокруг его оси до угловой скорости ω₀ и затем поместили в угол. Коэффициент трения между цилиндром и стенками равен k. Сколько времени цилиндр будет вращаться в этом положении?

1.4.6. Однородный диск радиуса R раскрутили до угловой скорости ω и осторожно положили на горизонтальную поверхность. Сколько времени диск будет вращаться на поверхности, если коэффициент трения равен k?

1.4.7. Гладкий однородный стержень AB массы M и длины l свободно вращается с угловой скоростью ω₀ в горизонтальной плоскости вокруг неподвижной вертикальной оси, проходящей через его конец A. Из точки A начинает скользить по стержню небольшая муфта массы m. Найти скорость муфты относительно стержня в тот момент, когда она достигнет его конца B.

1.4.8. Горизонтально расположенный однородный диск массы M и радиуса R свободно вращается вокруг вертикальной оси, проходящей через его центр. Диск имеет радиальную направляющую, вдоль которой может скользить без трения небольшое тело массы m. К телу привязана нить, пропущенная через полую ось диска вниз. Первоначально тело находилось на краю диска, и вся система вращалась с угловой скоростью ω₀. Затем к нижнему концу нити приложили силу F, с помощью которой тело медленно подтянули к оси вращения. Найти:

а) угловую скорость системы в конечном состоянии:

б) работу, которую совершила сила F.

1.4.9. Человек массы m ₁ стоит на краю горизонтального однородного диска массы m ₂ и радиуса R, который может свободно вращаться вокруг неподвижной вертикальной оси, проходящей через его центр. В некоторый момент человек начал двигаться по краю диска, совершил перемещение на угол φ' относительно диска и остановился. Пренебрегая размерами человека, найти угол, на который повернулся диск

к моменту остановки человека.

1.4.10. Два горизонтальных диска свободно вращаются вокруг вертикальной оси, проходящей через их центры. Моменты инерции дисков относительно этой оси I ₁ и I ₂, угловые скорости ω₁ и ω₂. После падения верхнего диска на нижний оба диска из-за трения между ними начали через некоторое время вращаться как единое целое. Найти:

а) установившуюся угловую скорость вращения дисков;

б) работу, которую совершили при этом силы трения.

1.4.11. Двум одинакового радиуса дискам сообщили одну и ту же угловую скорость ω₀, а затем их привели в соприкосновение, и система через некоторое время пришла в новое установившееся состояние движения. Оси дисков неподвижны, трения в осях нет. Моменты инерции дисков относительно их осей вращения равны I ₁ и I ₂. Найти:

а) приращение момента импульса системы;

б) убыль ее механической энергии.

1.4.12. Однородный диск радиуса R и массы m лежит на гладкой горизонтальной поверхности. На боковую поверхность диска плотно намотана нить, к свободному концу K которой приложили постоянную горизонтальную силу F. После начала движения диска точка K переместилась на расстояние l. Найти угловую скорость диска к этому моменту.

1.4.13. Нити намотаны на концах однородного сплошного цилиндра массы m. Свободные концы нитей прикреплены к потолку кабины лифта. Кабина начала подниматься с ускорением a ₀. Найти ускорение a ' цилиндра относительно кабины и силу F, с которой цилиндр действует (через нити) на потолок.

1.4.14. Сплошному однородному цилиндру массы m и радиуса R сообщили вращение вокруг его оси с угловой скоростью ω₀, затем его положили боковой поверхностью на горизонтальную плоскость и предоставили самому себе. Коэффициент трения равен k. Найти:

а) время, в течение которого движение цилиндра будет происходить со скольжением;

б) полную работу силы трения скольжения.

1.4.15. Однородный шар радиуса г скатывается без скольжения с вершины сферы радиуса R. Найти угловую скорость шара после отрыва от сферы. Начальная скорость шара пренебрежимо мала.

1.4.16. Однородный стержень, падавший в горизонтальном положении с высоты h, упруго ударился одним концом о край массивной плиты. Найти скорость центра стержня сразу после удара.

1.4.17. Волчок, масса которого m = 1,0 кг и момент инерции относительно собственной оси I = 4,0 г·м², вращается с ω = 320 рад/с, Его точка опоры находится на подставке, которую перемещают в горизонтальном направлении с ускорением a = 3,0 м/с². Расстояние между точкой опоры и центром масс волчка l = 10 см. Найти модуль и направление вектора ω' — угловой скорости прецессии волчка.

1.4.18. Корабль движется со скоростью = 36 км/ч по дуге окружности радиуса R = 200 м. Найти момент гироскопических сил, действующих на подшипники со стороны вала с маховиком, которые имеют момент инерции относительно оси вращения I = 3,8·10³ кг·м² и делают n = 300 об/мин. Ось вращения расположена вдоль корабля.

1.4.19. Волчок массы m = 0,50 кг, ось которого наклонена под углом к вертикали, прецессирует под действием силы тяжести. Момент инерции волчка относительно его оси симметрии I = 2,0 г·м², угловая скорость вращения вокруг этой оси ω = 350 рад/с, расстояние от точки опоры до центра масс волчка l = 10 см. Найти:

а) угловую скорость прецессии волчка;

б) модуль и направление горизонтальной составляющей силы реакции, действующей на волчок в точке опоры.

1.4.20. Локомотив приводится в движение турбиной, ось которой параллельна осям колес. Направление вращения турбины совпадает с направлением вращения колес. Момент инерции ротора турбины относительно собственной оси I = 240 кг·м². Найти добавочную силу давления на рельсы, обусловленную гироскопическими силами, когда локомотив идет по закруглению радиуса R = 250 м со скоростью = 50 км/ч. Расстояние между рельсами l = 1,5 м. Турбина делает n = 1500 об/мин.

Date: 2016-06-06; view: 3917; Нарушение авторских прав