Основное уравнение динамики

КИНЕМАТИКА

1.1.1. Минометная батарея расположена у подножья горы с наклоном к горизонту 45°. Под каким углом α к горизонту надо установить ствол орудия, чтобы мина достигла склона на максимальной высоте? Сопротивление воздуха не учитывать.

1.1.2. Под каким углом φ к горизонту следует бросить камень с вершины горы с уклоном 45°, чтобы он упал на склон на максимальном расстоянии?

1.1.3. Атлет толкает ядро с разбега. Считая, что скорость ядра относительно атлета в момент броска равна по величине скорости разбега, найти угол α, под которым следует выпустить ядро по отношению к земле, чтобы дальность полета была максимальной. Высоту самого атлета не учитывать.

1.1.4. Два тела бросили одновременно из одной точки: одно — вертикально вверх, другое — под углом к горизонту. Начальная скорость каждого тела 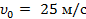. Пренебрегая сопротивлением воздуха найти расстояние между телами через .

1.1.5. Два шарика бросили одновременно из одной точки в горизонтальном направлении в противоположные стороны со скоростями и . Найти расстояние между шариками в момент, когда их скорости окажутся взаимно перпендикулярными.

1.1.6. Три точки находятся в вершинах равностороннего треугольника со стороной a. Они начинают одновременно двигаться с постоянной по модулю скоростью , причем первая точка все время держит курс на вторую, вторая — на третью, третья — па первую. Через сколько времени точки встретятся?

1.1.7. Точка A движется равномерно со скоростью так, что вектор все время нацелен на точку B, которая движется прямолинейно и равномерно со скоростью 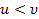. В начальный момент и расстояние между точками равно l. Через сколько времени точки встретятся?

1.1.8. Две частицы движутся с постоянными скоростями и по двум взаимно перпендикулярным прямым к точке их пересечения O. В момент частицы находились на расстояниях и от точки O. Через сколько времени после этого расстояние между частицами станет наименьшим? Чему оно равно?

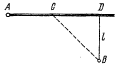1.1.9. Из пункта A, находящеюся на шоссе, необходимо за кратчайшее время попасть на машине в пункт B, расположенный в поле на расстоянии l от шоссе. На каком расстоянии от точки D следует свернуть с шоссе, если скорость машины по полю в раз меньше ее скорости по шоссе?

1.1.10. За время точка прошла половину окружности радиуса R = 160 см. Найти за это время:

а) среднее значение модуля скорости ;

б) модуль среднего вектора скорости ;

в) модуль среднего вектора полного ускорения , если тангенциальное ускорение постоянно.

1.1.11. Точка движется по окружности со скоростью , где . Найти её полное ускорение в момент, когда она пройдет длины окружности после начала движения.

1.1.12. Точка движется по дуге окружности радиуса R. Её скорость зависит от пройденного пути по закону . Найти угол между векторами скорости и полного ускорения как функцию .

1.1.13. Твердое тело вращается, замедляясь, вокруг неподвижной оси с угловым ускорением , где — его угловая скорость. Найти среднюю угловую скорость тела за время, в течение которою оно будет вращаться, если в начальный момент его угловая скорость была равна .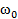

1.1.14. Как показали радиолокационные измерения, Венера вращается вокруг своей оси в направлении, обратном ее орбитальному движению. Период осевого вращения Венеры (относительно звезд) T₁ = 243 земных суток. Венера обращается вокруг Солнца с периодом T₂ = 225 земных суток. Определить продолжительность солнечных суток на Венере, т. е. время T между двумя последовательными прохождениями Солнца через один и тот же меридиан на этой планете (время от полудня до полудня).

1.1.15. Колесо радиуса R катится без проскальзывания по горизонтальной поверхности со скоростью . Найти величину и направление векторов скорости и 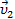для двух точек обода катящегося колеса, расположенных в данный момент на противоположных концах горизонтального диаметра колеса. Как будут направлены ускорения этих точек?

1.1.16. Автомобиль с колесами радиусом R движется со скоростью по горизонтальной дороге, причем , где — ускорение свободного падения. На какую максимальную высоту h может быть заброшена вверх грязь, срывающаяся с колес автомобиля? Указать положение той точки на покрышке колеса, с которой при данной скорости движения автомобиля грязь будет забрасываться выше всего. Сопротивление воздуха движению отброшенной вверх грязи не учитывать.

1.1.17. Колесо радиуса R катится без проскальзывания по горизонтальной поверхности со скоростью . Найти горизонтальную и вертикальную компоненты вектора ускорения произвольной точки на ободе колеса. Указать величину и направление вектора полного ускорения точек, лежащих на ободе колеса.

1.1.18. Колесо радиусом R движется горизонтально со скоростью и вращается с угловой скоростью . Точка A на ободе описывает в пространстве некоторую траекторию. Найти радиус ее кривизны в момент, когда точка находится на уровне центра колеса.

1.1.19. Диск радиусом R, вращающийся вокруг своей оси с угловой скоростью , брошен под углом α к горизонту со скоростью . Точка A на ободе описывает в пространстве некоторую траекторию. Найти радиус се кривизны в момент наибольшего подъема, если точка A находится при этом над центром диска.

1.1.20. Горизонтальный диск вращается с угловой скоростью вокруг вертикальной оси. В некоторой точке на этом диске на расстоянии R от его оси установлен второй диск, ось которого также вертикальна. Второй диск вращается вокруг своей оси в ту же сторону, что и первый диск, но с угловой скоростью 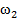. Где располагается та мгновенная ось вращения, движение вокруг которой второго диска будет эквивалентно его участию в двух описанных вращательных движениях с угловыми скоростями и 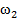? С какой угловой скоростью должен вращаться второй диск вокруг этой мгновенной оси?

ОСНОВНОЕ УРАВНЕНИЕ ДИНАМИКИ

1.2.1. По наклонной плоскости, составляющей угол α с горизонтом, ускоренно скользит доска массой M. Коэффициент трения доски о наклонную плоскость равен k. На доску кладут тело массой m, которое скользит по доске без трения. Какова должна быть минимальная масса тела , чтобы движение доски по наклонной плоскости стало равномерным?

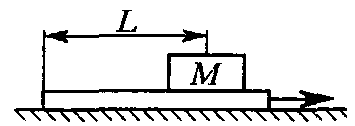1.2.2. Плоская шайба массой M лежит на тонкой пластине на расстоянии L от ее края. Пластину с большой постоянной скоростью выдергивают из-под шайбы, которая при этом практически не успевает сместиться. Найти зависимость 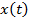расстояния, проходимого шайбой, от времени ее скольжения по поверхности стола. На какое расстояние в итоге сместится шайба? Считать, что сила трения между шайбой и пластиной, шайбой и столом прямо пропорциональна скорости с коэффициентом пропорциональности γ.

1.2.3. Хоккейная шайба падает на лед со скоростью под углом α и продолжает скользить по льду. Найти скорость скольжения как функцию времени, если коэффициент трения шайбы о лед k не зависит от скорости и силы давления шайбы на лед.

1.2.4. При торможении всеми четырьмя колесами тормозной путь автомобиля равен . Найти тормозные пути этого же автомобиля при торможении только передними и только задними колесами. Коэффициент трения скольжения 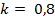. Центр масс автомобиля расположен на равном расстоянии от передних и задних колес и на высоте h = l /4, где l — расстояние между осями.

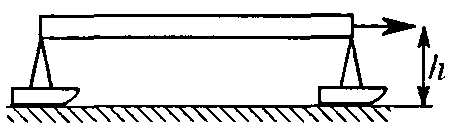1.2.5. Длинная однородная балка массой M и длиной l перевозится на двух коротких санях. Какую силу тяги нужно приложить для равномерного перемещения этого груза по горизонтали? Коэффициент трения для передних саней , для задних — . Сила тяги горизонтальна и приложена к балке на высоте h от поверхности земли. Массами саней пренебречь.

1.2.6. Два шарика падают в воздухе. Шарики сплошные, сделаны из одного материала, но диаметр одного из шариков вдвое больше другого. В каком соотношении будут находиться скорости шариков при установившемся (равномерном) движении? Считать, что сила сопротивления воздуха пропорциональна площади поперечного сечения движущегося тела и квадрату его скорости.

1.2.7. Тело бросают вертикально вверх в вязкой среде. Сила вязкого трения пропорциональна скорости движения тела, а установившаяся скорость этого теле в этой среде равна . Вычислить время t ₁ подъема тела на максимальную высоту его полета вверх и сравнить его со временем t ₀ подъема на максимальную высоту в отсутствие трения. Начальная скорость тела в обоих случаях одинакова и равна .

1.2.8. Из зенитной установки выпущен снаряд вертикально вверх со скоростью . Сила сопротивления воздуха . Определить максимальную высоту H подъема снаряда и время его подъема τ до этой высоты, если известно, что при падении снаряда с большой высоты его установившаяся скорость .

1.2.9. Из одного неподвижного облака через τ секунд одна за другой начинают падать две дождевые капли. Как будет изменяться со временем расстояние между ними? Решить задачу в двух случаях: 1) полагая, что сопротивление воздуха отсутствует; 2) полагая, что сопротивление воздуха пропорционально скорости капель.

1.2.10. С палубы яхты, бороздящей океан со скоростью 10 узлов (18 км/ч), принцесса роняет в воду жемчужину массой m = 1 г. Как далеко по горизонтали от места падения в воду может оказаться жемчужина на дне океана, если при ее движении в воде сила сопротивления ; ?

1.2.11. Брусок скользит по гладкой горизонтальной поверхности со скоростью и по касательной попадает в область, ограниченную вертикальным забором в форме полуокружности. Определить время, через которое брусок покинет эту область. Радиус забора R, коэффициент трения скольжения бруска о поверхность забора k. Трением бруска о горизонтальную поверхность пренебречь, размеры бруска много меньше R.

1.2.12. Автомобиль движется с постоянной скоростью 90 км/ч по замкнутой горизонтальной дороге, имеющей форму эллипса с полуосями 500 м и 250 м. На каких участках дороги ускорение автомобиля максимально и минимально? Чему равны максимальное и минимальное ускорения? Каков должен быть коэффициент трения между полотном дороги и шинами автомобиля, чтобы автомобиль при движении по эллипсу не заносило?

1.2.13. Шарик массой m, подвешенный на невесомой и нерастяжимой нити, лежит на поверхности гладкой сферы радиусом R. Точка подвеса находится на вертикальном стержне AO, жестко связанном c центром сферы. Для неподвижной сферы отношение силы натяжения нити и реакции сферы равно α, а отношение силы тяжести и натяжения нити — β. Вычислить угловую скорость вращения системы вокруг вертикальной оси, при которой сила давления шарика на сферу станет равной нулю. Шарик считать точечным.

1.2.14. Шарик массой m, подвешенный на нити длиной l, лежит на поверхности гладкой сферы радиусом R. Расстояние от точки подвеса до центра сферы равно d. Вычислить натяжение нити и реакцию сферы для неподвижного шарика. Определить скорость , которую надо сообщить шарику в направлении, перпендикулярном плоскости чертежа, чтобы реакция сферы стала равной нулю. Шарик считать точечным. Нить невесома и нерастяжима.

1.2.15. На врытый в землю столб навита веревка. За один конец веревки тянут с силой F = 10 000 H. Какую силу надо приложить к другому концу веревки, чтобы она не проскальзывала при натяжения? Коэффициент трения веревки о столб k = 1/π. Веревка обвита вокруг столба 2 раза.

1.2.16. Нить перекинута через бревно. На концах нити укреплены грузы, имеющие массы m ₁ и m ₂. Считая заданным коэффициент трения k нити о бревно, найти условие, при котором грузы будут оставаться в покое. Определить ускорение a системы грузов при нарушении условий равновесия.

1.2.17. Твердый шарик массой m находится в вязкой среде на расстоянии L от вертикальной стенки. Шарик щелчком посылается к стенке с достаточно большой начальной скоростью . Считая, что сила сопротивления , найти на какое максимальное расстояние L ₁ отскочит шарик после упругого удара о стенку. Силой тяжести пренебречь.

1.2.18. Шарик массой m запущен под углом Θ к горизонтальной плоскости. При движении шарик испытывает трение со стороны среды, . Начальная скорость шарика равна . На каком расстоянии Ь от места запуска и за какое время шарик достигнет максимальной высоты?

1.2.19. Из неподвижного аэростата через τ секунд вслед за первым выпрыгивает второй парашютист. Оба с нулевой начальной скоростью и с одинаковой массой m. Как будет изменяться со временем расстояние между ними, если сопротивление воздуха пропорционально скорости парашютистов (коэффициент пропорциональности равен )?

1.2.20. С летящего прямолинейно и параллельно поверхности Земли самолета сбрасывают груз массой m с нулевой относительно самолета скоростью. Как далеко от места сбрасывания может оказаться груз на земле, если при его движении в воздухе сила сопротивления , а скорость самолета равна .

Date: 2016-06-06; view: 4102; Нарушение авторских прав