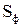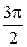Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

III. Приложения определенного интеграла
|
|
1. С помощью определенного интеграла можно вычислять площади плоских фигур, ограниченных кривыми. Напомним, что кривые могут быть заданы различными способами, т.е.
1) в прямоугольных декартовых координатах (в явном виде и параметрически);
2) в полярных координатах.
Рассмотрим случаи вычисления площадей плоских фигур в прямоугольных координатах.
а) если фигура представляет из себя криволинейную трапецию вида.

  
 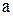   Рисунок 5
Рисунок 5
|
 ; ;
|
б) если криволинейная трапеция расположена ниже оси  , т.е.
, т.е. 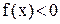 тогда исходя из свойств определенного интеграла
тогда исходя из свойств определенного интеграла
Рисунок 6 |
 . .
|
В общем случае  ;
;
в) если плоская фигура имеет сложную форму, т.е. прямые  «вырождаются» в точки, то фигуру следует разбить на части так, чтобы можно было применить известные формулы.
«вырождаются» в точки, то фигуру следует разбить на части так, чтобы можно было применить известные формулы.
Проиллюстрируем некоторые возможные варианты:
 

 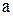  
 Рисунок 7
Рисунок 7
|
 ; ;
|
г)
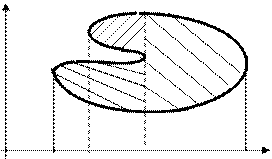 



 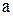     Рисунок 8
Рисунок 8
|
 ; ;
|
д) если криволинейная трапеция ограничена прямыми  и
и
 , осью
, осью  и непрерывной кривой
и непрерывной кривой  , то
, то 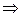
 
 

  Рисунок 9
Рисунок 9
|
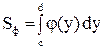 . .
|
Рассмотрим примеры нахождения площади плоских фигур:
Пример 1. Найти площадь фигуры, ограниченной линиями: 
Решение.
 
    1 1 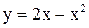
    
     0 1 0 1  2 3 2 3 
 - 1 - 1
 - 2 - 2 
 - 3 - 3
| а) Построим графики данных функций:
 - прямая; - прямая;
 - парабола; приведем ее уравнение к каноническому виду: - парабола; приведем ее уравнение к каноническому виду:
 ; ;
 ; ;
|
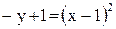 ;
;
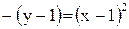 откуда координаты вершины
откуда координаты вершины  , ветви вниз. Находим точки пересечения параболы с осью
, ветви вниз. Находим точки пересечения параболы с осью  :
:
 ,
,  ,
,  или
или  ,
,  .
.
б) Чтобы найти площадь данной фигуры, разобьем ее на части. Для этого найдем координаты точек пересечения графиков, решив систему уравнений данных линий:


Тогда  (кв. ед).
(кв. ед).
 ;
;  (кв. ед.).
(кв. ед.).
 .
.
 (кв. ед).
(кв. ед).
в)  (кв. ед.)
(кв. ед.)
Замечание. Площадь этой же фигуры можно вычислить более рациональным способом, применив формулу

Ответ:  кв. ед.
кв. ед.
Пример 2. Вычислить площадь фигуры, ограниченной кривой 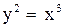 , прямой
, прямой  и осью Оу.
и осью Оу.
Решение.
 1
1 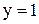 0 1
0 1  -1
Рисунок 10
-1
Рисунок 10
| а) Построим графики данных функций;
 - прямая, параллельная оси - прямая, параллельная оси  ; ;
 - полукубическая парабола. - полукубическая парабола.
|
б) Для вычисления площади этой фигуры воспользуемся случаем, когда кривая задана функциональной зависимостью  . Выразим
. Выразим  через
через  :
:
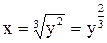 .
.
Тогда  (кв. ед.).
(кв. ед.).
Ответ:  кв. ед.
кв. ед.
Замечание. Если линия, ограничивающая криволинейную трапецию, задана параметрически, то

Пример 3. Вычислить площадь фигуры, ограниченной линиями:  , прямой
, прямой  и осью
и осью  .
.
Решение.
Построим графики данных функций. Так как одна из линий задана параметрически, то придавая параметру произвольные значения, составим таблицу значений функции.
1
0 1 -1
| Таким образом, считая
 найдем найдем  , подставим найденные выражения в формулу, предварительно вычислив пределы интегрирования по , подставим найденные выражения в формулу, предварительно вычислив пределы интегрирования по  : :
 (в нашем случае
(в нашем случае  ). ).
 (в нашем случае
(в нашем случае  ).
Тогда ).
Тогда 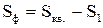 , так как , так как  кв. ед.; кв. ед.;
| ||||||||||||||||||
 (кв. ед.).
(кв. ед.).
 кв. ед.
кв. ед.
Ответ:  кв. ед.
кв. ед.
2. Вычисление площадей плоских фигур в случае, когда линии, их ограничивающие, заданы в полярной системе координат.
Если непрерывная кривая задана в полярных координатах уравнением  , то площадь сектора АОВ вычисляется по формуле:
, то площадь сектора АОВ вычисляется по формуле:
 В В  А
А
 0
0  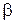   Рисунок 11
Рисунок 11
|
 . .
|
Пример 4. В полярной системе координат построить фигуру, ограниченную указанной линией, и вычислить ее площадь: 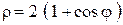 .
.
Решение.
а) Составим таблицу значений  задавая шаг для
задавая шаг для  .
.

0,6
0 4 0,6
Рисунок 12 График этой функции – кардиоида. |
|
б) Вычислим  , т.к.
, т.к. 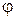 изменяется от 0 до
изменяется от 0 до  (см. рис. 12), т.к. фигура симметрична относительно Ох, где
(см. рис. 12), т.к. фигура симметрична относительно Ох, где


Ответ:  кв. ед.
кв. ед.
Date: 2016-05-25; view: 447; Нарушение авторских прав