Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?
Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника
Толқындық функция және оның қасиеті
|
|
Кеңістікте берілген нүктедегі Де - Бройль толқынының интенсивтілігі, микробөлшектердің дифракциясы туралы әдісті куәландыратын осы нүктеге түсірілетін бөлшектердің санымен байланысты. Сондықтан микробөлшектердің толқындық қасиеті оларды бейнелеудің статистикалық (ықтималдылық) жақындауын талап етеді.
Квантық жүйелердің көрсеткішін бейнелеу үшін толқындық функция (басқаша атауы – пси-функция)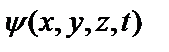 
енгізіледі. Ол ықтималдылықтың 
, бөлшек dV элемент көлемінде мынаған тең болуымен анықталады:
функциясының физикалық мағынасы бұл функцияның өзі емес, де -Бройль толқынының интенсивтілігімен берілетін оның модулінің квадратына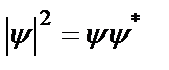 
(мұндағы 
- 
- мен комплексті түйіндес функция) ие. 
шамасы pw ықтималдық тығыздығы мағынасына ие, ал 
толқындық функциясының өзі ықтималдық амплитудасы мағынасына ие. Ықтималдықты нөмірлеу шарты бөлшектің бар болу ықтималдығының кеңістіктің әйтеуір бір жерінде бірге тең болуынан (интеграл барлық шексіз кеңістік бойынша шығарылады)алынады.
Элемент көлеміндегі микробөлшектердің әсерінен табылу ықтималдығын сипаттайтын толқындық функция, 1) шектеулі (ықтималдық бірден үлкен болуы мүмкін емес), 2) бірмәнді (ықтималдық бірмәнді шама болмауы мүмкін емес), 3) үздіксіз (ықтималдық секіріп өзгеруі мүмкін емес).
Толқындық функция берілген микрообъектілерді сипаттайтын физикалық мәндердің орташа шамасын есептеуге ерік береді. Мысалы, орташа арақашықтық 
мына түрге ие:
, 
.
Толқындық функция суперпозиция принципін қанағаттандырады:
Егер жүйе 
толқындық функциялармен бейнеленетін әртүрлі күйлерде болатын болса, онда ол да сол сияқты осы функциялардың сызықтық комбинациясымен бейнеленетін күйде болады (мұндағы Cn (n=1,2,…) – туынды, негізінен айтқанда комплексті сандар).
Ықтималдықтар емес (толқындық функциялардың модулінің квадратымен анықталатын), тәуелсіз жағдайлар үшін ықтималдықты қосу теоремасы әділ толқындық функцияларды қосу (ықтималдықтар амплитудасы), кванттық теорияны классикалық статистикалық теориядан принципиальды ерекшелейді.
Date: 2016-05-25; view: 2287; Нарушение авторских прав