
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Часть 2. Локальная фильтрация изображений
|
|
Цель работы: Изучение локальной фильтрации.
Необходимые теоретические сведения
Принципы локальной фильтрации
Алгоритмы локальной фильтрации объединены общей идеей фильтрации скользящим окном, или апертурой. Термин «локальная» подчеркивает тот факт, что размеры окна по обеим осям меньше соответствующих размеров фильтруемого изображения.
Цели локальной фильтрации обычно состоят в улучшении качества изображения; чаще всего это устранение помех или повышение резкости, подчеркивание контуров.
Фильтрация изображений имеет свои особенности по сравнению с фильтрацией радио – и аудиосигналов. Эти особенности связаны с двумерной природой самого изображения, которая приводит и тому, что вместо одномерных фильтров, предназначенных для фильтрации сигналов одной переменной, при фильтрации изображений применяют двумерные фильтры.
Такой двумерный фильтр устроен следующим образом. Берется небольшой, обычно прямоугольный, участок плоскости и на нем определяется некоторая функция. Упомянутый участок называется апертурой, или окном, а заданная на нем функция - весовой функцией, или функцией окна. Таким образом, каждому элементу апертуры соответствует (присваивается пользователем) определенное число, называемое в дальнейшем весовым множителем. Совокупность всех весовых множителей и составляет весовую функцию. Апертура вместе с заданной на ней весовой функцией часто называется маской. Немаловажным достоинством последнего термина является его краткость.
Обычно используются апертуры небольшого размера 3×3 элемента; увеличение размеров апертуры существенно увеличивает объем вычислений, в то время как качество обработки улучшается незначительно. Хотя при современной производительности компьютеров используются апертуры размером 5×5, 7×7 элементов и даже больше. Линейные размеры апертуры обычно берутся нечетными, чтобы можно было однозначно указать ее центральный элемент.
Виды локальной фильтрации
В зависимости от того, куда (в какое поле) записывается отклик фильтра, различают простые и рекурсивные фильтры. Если в простых (нерекурсивных) фильтрах отклик записывается в выходное изображение, то в рекурсивных он записывается обратно в исходное изображение, изменяя значение пикселей непосредственно в процессе фильтрации. Поэтому в рекурсивных фильтрах уже обработанные пиксели влияют на результат фильтрации последующих.
Иногда оказывается полезным многократное повторение процедуры фильтрации; в этих случаях говорят об итеративном применении фильтров (не путать с рекурсивными фильтрами!).
В локальной фильтрации используются линейные и нелинейные фильтры. Характер фильтра зависит от операций, выполняемых в каждом положении окна. В линейных фильтрах отклик является линейной функцией нескольких переменных, роль которых играют попавшие в окно пиксели. Весовые множители – это коэффициенты упомянутой линейной функции. Фильтры, в которых отклик не может быть выражен линейной функцией от значений элементов изображения, являются по определению нелинейными.
При линейной фильтрации с помощью оконных функций различают два случая:
1. сумма коэффициентов SK оконной функции отлична от нуля. Импульсный отклик такого фильтра имеет низкочастотный характер и поэтому содержит постоянную составляющую, т.е. фоновую компоненту. Для получения этой компоненты значения коэффициентов следует делить на величину SK;
2. сумма коэффициентов SK = 0. Фильтр имеет высокочастотный характер и служит для выделения верхних пространственных частот (повышения резкости изображений, выделения контуров и т.д.). Импульсный отклик содержит отрицательные составляющие, которые не могут быть представлены в результирующем изображении с положительными значениями полутонов. Поэтому при воспроизведении результирующего изображения необходимо сдвинуть уровень черного на величину G /2 и уменьшить динамический диапазон изменения яркости до G /2.
Существует так называемый краевой эффект, который редко упоминается: способ обработки пикселей, лежащих вблизи границ поля [2, 4], когда маска фильтра простирается за пределы изображения. Возникает некоторые сложности, поскольку упускаются пограничные точки изображения.
Влияние краевых эффектов особенно ощутимо на небольших изображениях. Если размер изображения много больше размера окна, то доля площади профильтрованного поля, на которой заметны краевые эффекты, мала. В этом случае краевыми эффектами можно пренебречь и выбирать алгоритм обработки из других соображений, например по максимуму быстродействия.
Линейная фильтрация изображений
Отклик линейного фильтра линейным образом зависит от обрабатываемого изображения. Алгоритм линейной фильтрации состоит, в общих чертах, в следующем. Последовательность значений выходного изображения Q формируется путем дискретной свертки входного поля f с функцией окна h (i, j), для задания которой используются локальные операторы (рис. 2).

|
| Рисунок 2 – Иллюстрация операции дискретной свертки с маской фильтра 3x3 |
По сути, функция окна h (i, j) является двумерной импульсной характеристикой фильтра. Фильтрация производится путем перемещения слева направо (или сверху вниз) окна (апертуры) на один пиксель. При каждом положении окна осуществляется перемножение весовых коэффициентов с соответствующими значениями исходного изображения, суммирование полученных произведений, нормирование результата суммирования (деления на нормирующий коэффициент) и присвоение центральному элементу окна полученного значения. Эти однотипные операции многократно повторяются для каждого положения окна.
Центр здесь выбирается потому, что в ином случае (если, например, присваивать значение отклика пикселю, соответствующему левому верхнему элементу окна) фильтрация сопровождается нежелательным сдвигом профильтрованного изображения относительно исходного. Упомянутый выше нормирующий коэффициент обычно (но не всегда) берется равным сумме всех элементов весовой функции (весовых множителей).
Функция окна определяется множеством весовых значений h (i, j), задаваемых для каждого (i, j) – го элемента окна.
Пусть окно имеет размер m × n элементов, текущий элемент, которого задается координатами (i, j)
| i = 0, 2,..., т -1 – текущая строка; j = 0, 2,..., п -1 – текущий столбец. | (5) |
Позиционирование окна на изображении определяется с помощью условного центра (I, J) окна (в системе координат окна). Условный центр определяется таким образом, что он при нечетных размерах окна совпадает с его центральным элементом:
 ; ;  , ,
| (6) |
где  обозначает целую часть от числа (функцию «антье»).
обозначает целую часть от числа (функцию «антье»).
Текущее положение окна на исходном изображении f обозначим через (p, q). Отклик фильтра присваивается той же точке (p, q) профильтрованного изображения Q. Массив пикселей выходного изображения Q формируется путем дискретной свертки входного изображения/и функции окна h (i, j)
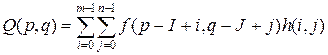 . .
| (7) |
Формула справедлива лишь при условии, что функция окна не выходит за пределы исходного изображения, т.е. выполняются условия (из-за краевого эффекта)
| I ≤ p ≤ N – m + i, J ≤ q ≤ M – n + j, | (8) |
где М, N – размеры изображения.
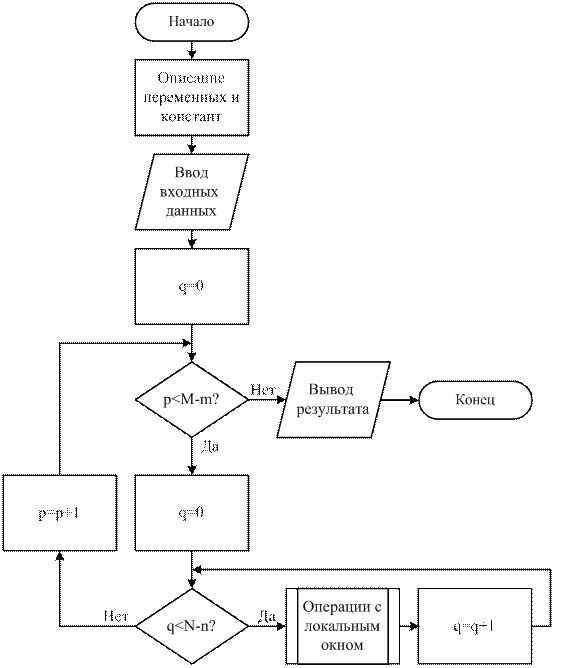
Алгоритм локальной фильтрации показан на рис. 3.
|
| Рисунок 3 – Алгоритм локальной фильтрации |
Рекурсивные линейные фильтры [2]
Фильтр, в котором отклик определяется только через входные значения, называется простым, или нерекурсивным. Именно такими были рассмотренные выше линейные фильтры.
Рекурсивным называется фильтр, в котором отклик определяется не только через входные значения, но и через выходные [27, 33].
В рекурсивных фильтрах могут использоваться те же весовые функции, что и в нерекурсивных.
Дадим два определения. Рекурсивным фильтром 1-го рода называется такой фильтр, у которого отклик в каждом положении окна формируется так же, как у простого фильтра, но записывается обратно во входной массив, который теперь одновременно играет роль выходного:
 . .
| (9) |
Формула аналогична (3), поэтому сделанные замечания справедливы и здесь.
Рекурсивным фильтром 2-го рода называется комбинированный фильтр, у которого отклик формируется как взвешенная сумма откликов нерекурсивного фильтра и рекурсивного фильтра 1-го рода:
 , ,
| (10) |
где Q(p, q) определяемся из (1), F (p, q) - из (10), k - коэффициент, определяющий вклады каждого из двух упомянутых фильтров.
Варьируя величиной k от 0 до 1, можно плавно менять характер фильтра; k = 0 соответствует простому фильтру, k = 1 - рекурсивному фильтру 1-го рода.
Для рекурсивных фильтров 1-го рода нет необходимости писать специальные программы - эти фильтры реализуются с помощью уже рассмотренных нами программ простых, нерекурсивных линейных фильтров.
Для этого достаточно указать один и тот же массив как для входного изображения, так и для выходного.
Подчеркнем (специально для программистов) - рекурсивный фильтр вовсе не предполагает рекурсивного вызова подпрограмм, т. е. понятие рекурсии имеет здесь несколько иной смысл, чем в программировании.
Линейные фильтры
Подавление шумов и сглаживание
Равномерный фильтр-маска
Поскольку шум пространственно декоррелирован, в его спектре, как правило, содержатся более высокие пространственные частоты, чем в спектре обычного изображения. Следовательно, простая низкочастотная пространственная фильтрация может служить эффективным средством подавления шумов. Ниже приведен один из сглаживающих оконных операторов с положительными элементами, часто называемыми шумоподавляющими масками [3]:
 . .
| (11) |
Функция hS 1 осуществляет усреднение по всем элементам, попавшим в окно.
Биномиальный фильтр (фильтр Гаусса)
Наименьшая маска биномиального фильтра имеет размер 3 х 3:
 . .
| (12) |
При маске 5х5:
 . .
| (13) |
Другие низкочастотные фильтры-маски
Кроме равномерной и биноминальной маски существуют и другие низкочастотные фильтры с малой маской:
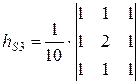 . .
| (14) |
Выходное значение фильтра с оператором hS 1 при некотором положении окна можно определить не только по (7), но и как
| y = 1/10 (xp –1, q –1 + xp –1, q + xp –1, q +1 + xp , q –1 + 2 xp , q + xp , q +1 + xp +1, q –1 + xp +1, q + xp +1, q +1), | (15) |
где xp , q – элементы входного (исходного) изображения, попавшие в окно фильтра (блок «Операции с локальным окном» рис. 3). Благодаря большему весовому коэффициенту центральный элемент изображения, попадающий в окно, выделяется сильнее.
С помощью рассмотренной выше биноминальной маски hS 2 (12), благодаря большим весам, подчеркиваются (выделяются) четырехсвязные элементы исходного изображения, т.е. горизонтальные и вертикальные линии. Если необходимо подчеркнуть диагональные линии, то следует выделить восьмисвязные элементы исходного изображения, не являющиеся четырехсвязными. Для этого целесообразно применять оконную функцию hS 4.

| (16) |
Нормирующие коэффициенты низкочастотных оконных функций (11) –(14), (16) выбраны таким образом, чтобы получить единичный коэффициент передачи. В результате процедура подавления шума не будет вызывать смещение средней яркости (интенсивности) обработанного изображения.
Существенным недостатком линейной фильтрации изображений является то, что наряду с уменьшением шумов одновременно происходит размывание контуров изображения. Это вызвано тем, что все элементы исходного изображения обрабатываются с одинаковым коэффициентом, т.е. линейные фильтры являются независимыми от структуры элементов и поэтому они не могут определить разницу между зашумленными и контурными элементами.
Чтобы уменьшить размывание изображения, целесообразно использовать метод селективного сглаживания. В ряде случаев, если яркость пикселей входного изображения распределена по нормальному закону, весьма эффективной при проведении предварительной обработки может оказаться сигма–фильтрация, при которой учитываются только те элементы входного изображения (находящиеся внутри окна), яркость которых находится в пределах Ех ±2σ. Здесь Ex – математическое ожидание, а σ – среднеквадратическое отклонение яркости пикселей изображения.
Сглаживающий фильтр Canny
Canny - оператор обнаружения границ. Был разработан в 1986 году Джоном Канни и использует многоступенчатый алгоритм для обнаружения границ в изображениях. Одним из этапов этого алгоритма является сглаживание шума. Для этого используется фильтр, который может быть хорошо приближен к первой производной Гауссианы σ = 1,4:
 . .
| (17) |
Нелинейная локальная фильтрация
Основные понятия теории локальной фильтрации справедливы и для локальной нелинейной фильтрации. Имеются в виду понятия процесса фильтрации, апертуры (двумерной и «линейной»), способы и алгоритмы перемещения апертуры по изображению; весовая функция применяется не всегда. Главное отличие нелинейной фильтрации от линейной заключается в том, что выходной сигнал формируется нелинейным образом от данных исходного изображения, а для рекурсивной фильтрации – нелинейным образом от отфильтрованного на предыдущих шагах изображения. В системах обработки изображения наиболее широкое применение находят два класса нелинейных фильтров. Фильтры, относящиеся к первому классу, используются для подавления шумов, а фильтры второго класса – для подчеркивания перепадов яркости.
Пороговая фильтрация
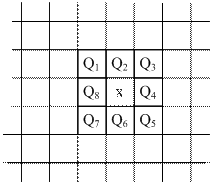
Шумы видеокамер или ошибки в канале передачи обычно проявляются на изображении как разрозненные изменения изолированных элементов, не обладающие пространственной корреляцией. Искаженные элементы часто весьма заметно отличаются от соседних элементов. Это наблюдение послужило основой для многих алгоритмов, обеспечивающих подавление шума. Рис. 4 поясняет простой пороговый метод. При таком алгоритме подавления шума последовательно измеряют яркость всех элементов изображения. Если яркость некоторого элемента превышает по модулю среднюю яркость группы ближайших элементов на некоторую пороговую величину, яркость элемента заменяется на среднюю яркость [3].
| Если 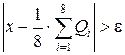 , то , то  . (18) . (18)
|
| Рисунок 4 – Пример порогового алгоритма подавления шума |
В качестве еще одного примера приведем алгоритм, который выявляет имеющиеся на изображении локальные максимумы (вершины). По изображению перемещается окно заданного размера. Пиксели, попавшие в окно, сравниваются по величине с пикселем, соответствующим центру окна. Если центральный пиксель больше или равен своему окружению, то он без изменения переносится в выходное изображение. Если хотя бы один пиксель в окне превышает центральный, в выходное поле записывается нуль.
Медианная фильтрация (МФ)
Использование алгоритмов линейной фильтрации имеет две особенности.
Первая заключается в том, что линейная фильтрация приводит к размыванию (сглаживанию) резких перепадов яркости изображений, прошедших обработку. Этот недостаток принципиально не может быть исключен в рамках линейной обработки. Причиной является то, что реальные изображения глобально не подчиняются гауссовскому распределению вероятностей (из-за наличия у изображений разнообразных границ, перепадов яркости, переходов от одной текстуры к другой и т.п.). Линейные же процедуры являются оптимальными при гауссовском распределении сигналов, помех и наблюдаемых данных. Хотя в пределах ограниченных участков изображения и поддаются локальному гауссовскому описанию.
Вторая особенность связана с тем, что кроме шумовых помех, которые обычно подчиняются гауссовскому распределению и эффективно подавляются линейной фильтрацией, на изображении могут присутствовать помехи другого рода. Например, импульсные помехи, при воздействии которых на изображении наблюдаются белые и/или черные точки, хаотически разбросанные по кадру. Такими помехами являются "битые" и "горячие" пиксели при цифровой съемке, "снеговой" шум, когда часть пикселей заменяется на пиксели с максимальной интенсивностью, и т.п. Применение линейной фильтрации в этом случае неэффективно – линейные операторы как бы размазывают такие помехи на всю площадь кадра.
Довольно эффективным решением перечисленных проблем является применение медианной фильтрации. Процедура состоит в следующем:
1. пиксели, попавшие в апертуру окна, сортируются в порядке возрастания яркости;
2. производится замена значения опорной точки (х, у) (находится в центре апертуры) величиной яркости пиксела, расположенного в середине (на медиане) этого ряда.
Формальное обозначение описанной процедуры имеет вид:
| Q = med(f 1, f 2, …, fn), | (19) |
где n – количество элементов изображения, попавших в апертуру.
В силу того что для операции нахождения медианы не выполняется одна из аксиом линейности, медианный фильтр является нелинейным [5]:
1. Для медианной фильтрации med{f} справедливы правила вычисления, которые описывают суммирование константы со значением последовательности и умножение последовательности на некоторый коэффициент a:
med{ a + f (n)} = a + med{ f (n)};
и
med{ af (n)} = a med { f (n)}.
2. Однако не является справедливым, что медианное значение суммы двух последовательностей равна сумме их медианных значений, т.е. правило
med{ f 1(n)+ f 2(n)} = med{ f 1(n)}+ med{ f 2(n)}
не соблюдается. Поэтому-то медианный фильтр и является нелинейным.
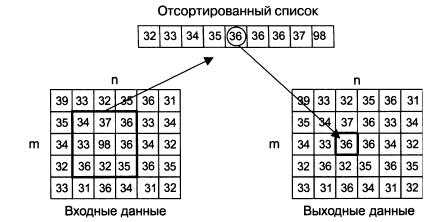
Например, если фрагмент изображения, попавший в окно фильтра, имеет вид (рис.6,б слева), то после медианной фильтрации его опорный элемент принимает значение 36 вместо исходного 98 (рис.6,б справа).
 а)
а)
|
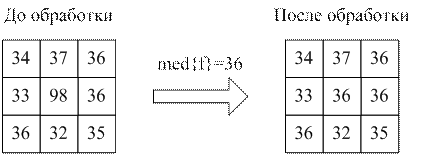 б)
б)
|
| Рисунок 6 – Иллюстрация принципа медианной обработки фрагмента изображения маской 3x3 |
Исходная выборка имеет вид: f = {34,37,36,33, 98,36,36,32,35}, а элемент 98, расположенный в ее центре, соответствует текущей точке фильтрации (x, y) (рис. 6). Большое значение яркости в этой точке кадра может быть результатом воздействия импульсной (точечной) помехи. Упорядоченная по возрастанию выборка имеет при этом вид {32,33,34,35, 36,36,36,37,98}, следовательно, в соответствии с процедурой (13), получаем Q = med(f 1, f 2, …, fn) = 38. Видно, что влияние “соседей” на результат фильтрации в текущей точке привело к “игнорированию” импульсного выброса яркости, что следует рассматривать как эффект фильтрации.
Медианный фильтр не оказывает влияние на ступенчатые и линейно–изменяющиеся сигналы. При этом подавляет импульсные выбросы исходного изображения, если длительность импульса составляет менее половины ширины окна. Т.е. при увеличении размеров импульсных помех необходимо увеличивать размер апертуры. Но (и это обратная сторона данного метода) может происходить полное исчезновение мелких деталей изображения при неадекватном выборе параметров фильтра.
Медианные фильтры нередко применяются итеративно, причем обработка повторяется до тех пор, пока на профильтрованном изображении не прекратятся изменения.
Действие МФ состоит в удалении экстремальных значений входной выборки - как положительных, так и отрицательных выбросов. Такой принцип подавления помехи может быть применен и для ослабления шума на изображении. Однако исследование подавления шума при помощи медианной фильтрации показывает, что ее эффективность при решении этой задачи ниже, чем у линейной фильтрации
Медианная фильтрация представляет собой эвристический метод обработки, ее алгоритм не является математическим решением строго сформулированной задачи. Поэтому исследователями уделяется большое внимание анализу эффективностиобработки изображений на ее основе и сопоставлению с другими методами.
Существует несколько разновидностей МФ, некоторое из них описаны в Приложении 2.
Подчеркивание перепадов яркости и границ
Сглаживающие фильтры подавляют верхние частотные компоненты изображения, что приводит не только к уменьшению влияния шума, но и к потере мелких объектов изображения. Во многих задачах распознавания образов необходимо выделять границы объектов, подчеркивать перепады яркостей, селектировать мелкие объекты. Для реализации таких задач используются так называемые дифференциальные операторы. В таких операторах сумма элементов оконной функции h равна нулю, что свидетельствует о том, что в зонах изображения с постоянной яркостью они дают нулевой отклик.
Широко применяются градиентные операторы Превита:
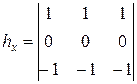 ; ;  ; ;
| (20) |
Собела:
 ; ; 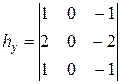 ; ;
| (21) |
Кирша:
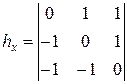 ; ; 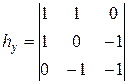 . .
| (22) |
Рассмотренные выше дифференциальные операторы выделяют более сильно вертикальные или горизонтальные линии, т.е. они зависимы от направления.
Другим видом зависимых от направления операторов являются так называемые компасс–градиентные (7). Название географического направления говорит о направлении перепада, которое вызывает максимальный отклик фильтра.
 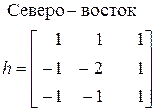
 
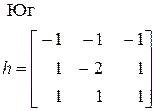 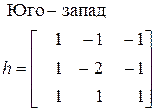
 
| (23) |
Для обнаружения линий (выделения перепадов) без указания их ориентации или для фокусировки изображений во многих случаях целесообразно использовать оператор Лапласа (лапласиан). Оконные функции Лапласа имеет вид:
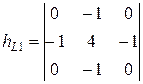 ; ; 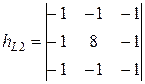 ; ;  . .
| (24) |
Оператор Лапласа обладает инвариантностью к повороту изображений, т.е. на одном и том же изображении он дает один и тот же результат независимо от ориентации этого изображения.
Эффект улучшения резкости изображения достигается за счет того, что сначала изображение усредняется, а затем из него вычитается исходное. В результате линии границ на изображении становятся более резкими.
Следовательно, на исходном изображении границы усиливаются, т.к. к ним прибавляются высокочастотные компоненты. Поэтому вычитание лапласиана из исходного изображения приводит к улучшению фокусировки последнего. Обычно такой же эффект дает вычитание из исходного изображения взвешенного среднего.
При обработке изображений очень часто используют последовательность фильтров: низкочастотный + Лапласа.
Еще одной группой фильтров, подчеркивающих границы и повышающих резкость изображения (в частотной интерпретации – это высокочастотные фильтры), используются следующие типовые весовые функции:
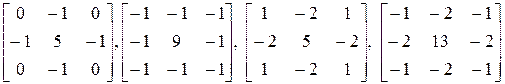 . .
| (25) |
Сумма весовых множителей здесь равна единице. Границы подчеркиваются независимо от их направления.
Указания к выполнению
Вывод изображения bmp из файла на экран: Вставка > Рисунок (или Картинка). И в левом нижнем углу появившейся области указать в кавычках путь к файлу, например “d:\4.bmp”.
Чтение изображения bmp в матрицу выполняется командой T:=READBMP(“путь_к_файлу\имя файла”).
Вывод матрицы считанного изображения на экран T=.
Вывод изображения bmp из матрицы на экран: Вставка > Рисунок (или Картинка). И в левом нижнем углу появившейся области указать имя матрицы, в данном случае T.
Для произведения операций необходимо знать размер прочитанного изображения (размерность матрицы; MathCAD сам выделит необходимый объем памяти). Для этого используются команды:
Возврат числа строк матрицы <имя переменной>:=rows(<имя матрицы>);
Возврат числа столбцов матрицы <имя переменной>:=cols(<имя матрицы>).
Изображение выведенное из матрицы будет в градациях серого с максимальной яркостью 255. Для его преобразования в черно-белое можно использовать разные принципы, например, все значения яркости меньше половины максимального обнулить, а всем значениям выше половины -присвоить максимальное значение.
Порядок выполнения работы
Данная работа выполняется на ПЭВМ с использованием программы MathCAD.
1. Считать из файла на диске изображения (файлы указываются преподавателем).
2. С помощью формул (1) – (4) провести оценку параметров изображения.
3. Произвести контрастирование изображения по (6).
4. Произвести пороговую бинаризацию изображения (рис. 1.5). Для этого с помощью гистограммы определить порог.
5. С помощью фильтров (11) – (14), (16) – (19) произвести подавление шумов заданного исходного изображения. Сравнить результаты их работы.
6. Произвести подчеркивание перепадов яркости и границ заданного изображения, используя градиентные операторы (20) – (23) (по указанию преподавателя). Сравнить результаты их работы.
7. Используя оконные функции Лапласа (24), произвести фокусировку изображения.
8. Произвести повышение контрастности перепадов изображения, используя градиентные операторы (25). Сравнить результаты с п.6.
Оформление отчета
В отчете необходимо представить результаты хода работы.
Вопросы к лабораторной работе
1. Что подразумевают под понятием фильтрации графической информации?
2. В виде каких составляющие человек запоминает графическую информацию?
3. За что отвечают каждая из составляющей графической информации?
4. В каком виде представляется изображение в компьютере?
5. Что такое полутоновое и бинарное изображение?
6. Что является целью предварительной обработки видеоданных?
7. В чем сущность поэлементной обработки? Чем она отличается от локальной фильтрации?
8. Что представляет из себя контрастность изображения?
9. Что такое локальная и глобальная контрастность?
10. Что такое контрастное растягивание? В чем оно заключается?
11. Как выглядит градационная характеристика после контрастного растягивания?
12. В чем заключается смысл соляризации?
13. Что такое пороговая бинаризация изображения?
14. В каких случаях применяется бинаризация?
15. Как (с помощью чего) определяют порог бинаризации?
16. Приведите примеры препарирования изображения, кроме бинаризации.
17. В чем особенность линейной фильтрации изображения по сравнению с фильтрацией радио – и аудиосигналов?
18. Посредством каких функций осуществляется двумерная фильтрация?
19. Какой вывод о характере фильтра можно сделать по сумме коэффициентов его оконной функции?
20. С помощью каких фильтров подавляют шум в изображении или размывают изображение? Приведите пример оператора.
21. Какой недостатком линейной фильтрации изображений проявляется с уменьшением шумов?
22. Что целесообразно использовать, чтобы уменьшить размывание изображения при линейной фильтрации?
23. Что такое нелинейная фильтрация изображений?
24. Приведите примеры методов нелинейной локальной фильтрации.
25. В чем заключается смысл пороговой фильтрации?
26. Для борьбы с какого вида помехами эффективна медианная фильтрация? Почему?
27. В чем смысл медианной фильтрации?
28. Фильтры с какими оконными функциями используют для выделения границ объектов и подчеркивания перепадов яркостей? Приведите примеры операторов.
29. Результаты воздействия каких фильтров не зависят от поворота изображения?
30. Какие фильтры, кроме линейных, используют для повышения контрастности перепадов изображения? Приведите пример.
Список литературы
1. Бондарев В.Н., Трёстер Г., Чернега В.С. Цифровая обработка сигналов: методы и средства. Учеб. пособие для вузов. – 2-е изд. – Х.: Конус, 2001. –398 с.
2. Яншин В. В., Калинин Г. А. Обработка изображений на языке Си для IBM PC: Алгоритмы и программы. – М.: Мир, 1994. –242 с.
3. Прэтт Э. Цифровая обработка изображений: В 2-х книгах. Пер. с англ, –М.: Мир, 1982. Кн.1. – 312 с.
4. Яне Б. Цифровая обработка изображений. – Москва: Техносфера, 2007. – 584с.
5. Ярославский Л. П. Введение в цифровую обработку изображений. – М.: Сов. радио, 1979. –312 с.
6. Грузман И.С., Киричук В.С., Косых В.П., Перетягин Г.И., Спектор А.А. Цифровая обработка изображений в информационных системах: Учебное пособие.- Новосибисрк: Изд-во НГТУ, 2000. - 168.
7. Р. Гонсалес, P. Вудс. Цифровая обработка изображений. Москва: Техносфера, 2005. – 1072 с.
Приложение 1 Краевой эффект (аспект программирования)
Вопрос о краевых эффектах вряд ли можно назвать принципиальным, однако при программировании его необходимо как-то решать. В этой связи можно осуществить 3 схемы обработки. При фильтрации центральной зоны, в которой окно целиком помещается на изображении, все три схемы дают одинаковые результаты. Выбор схемы обработки краев в принципе никак не связан с типом движения окна, хотя сложность полученной программы может зависеть от их сочетания.
1 схема обработки соответствует случаю, когда окно (ни один его элемент) не может выходить за пределы фильтруемого поля.
2 схема обработки разрешает выход краев окна за пределы поля, требуется только, чтобы центр окна всегда находился внутри поля.
3 схема обработки соответствует фильтрации на тороидальной поверхности.
1 схема обработки ограничивается фильтрацией центральной зоны, оставляя края изображения необработанными. Так как результат фильтрации записывается в элемент выходного поля, соответствующий центру окна, то ширина необработанной зоны равна половине размера окна (по соответствующей координате) минус единица. Таким образом, фильтрация по 1 схеме приводит к уменьшению фактических размеров изображения на ширину необработанной каймы. Достоинство 1 схемы – простота программирования.
2 схема обработки устраняет указанный недостаток ценой некоторого усложнения алгоритма обработки. Так как при этом центр окна пробегает все пиксели исходного поля, то и на профильтрованном изображении не остается незаполненных элементов. Элементы апертуры, выходящие за границы поля, в обработке не участвуют, поэтому отклик фильтра формируется на основе меньшего числа пикселей, чем в центральной зоне. Иными словами, вблизи краев изображения фактический размер окна уменьшается. Краевой эффект сохраняется, хотя и в существенно ослабленном виде. Алгоритм, реализующий 2 схему, сложнее и быстродействие его хуже, чем в случае 1 схемы.
Существует другая разновидность 2 схемы. В описанном выше варианте при выходе части элементов окна за пределы изображения осуществляется «усечение» окна. В данном варианте поступают противоположным образом – окно не усекается, а расширяется изображение путем доопределения его за пределами своих границ на половину размера маски фильтра. Изображение вне своих границ полагается тождественно равным нулю или же в эту дополнительную область экстраполируются тем или иным образом уровни яркости по уровням яркости пограничной зоны, что должно дать лучшие результаты. Если выбирается какой-либо метод экстраполяции, приграничные пиксели получают слишком большой вес. Если положить пограничную область равной нулю, то вводятся горизонтальные и вертикальные контуры на границе изображения.
Третья схема обработки получается, если представить, что изображение определено не на плоскости, а на тороидальной поверхности.
Изображение сначала как бы скручивается в трубку, Так что его правый край примыкает к левому. При этом правый край сдвинут вниз относительно левого на один пиксель, так что конец первой строки примыкает не к ее началу, а к началу второй строки и т. д. Далее соединяется верхний край образовавшейся трубки с нижним так, чтобы за последним пикселем последней строки шел первый пиксель первой строки.
Получится тор, на который спирально намотан одномерный массив, содержащий изображение. Вместо тора можно представить бесконечную плоскость, на которой заданное изображение периодически повторяется.
Тороидальная интерпретация заметно упрощает программирование, так как перемещение центра окна по строкам изображения заменяется его продвижением по индексу одномерного массива, содержащего изображение. 3 схема обработки является одной из лучших в смысле быстродействия, однако и она не свободна от краевых эффектов, хотя и другого типа, нежели в 1 и 2 схемах. Краевой эффект здесь состоит в том, что объекты, находящиеся на одном краю изображения, влияют на обработку и оставляют свой след на противоположном краю, что может показаться противоестественным.
Таким образом, не существует совершенного метода для корректной обработки пикселей, близких к границе, с помощью операций над соседними элементами. Тем или иным образом вносятся ошибки. Единственным надежным способом избежать ошибок является гарантия того, что интересующие объекты сохраняют безопасное расстояние от границы, равное, по крайней мере, половине размера наибольшей маски, используемой при обработке изображения.
Приложение 2 Использование и разновидности медианной фильтрации
Медианные фильтры нередко применяются итеративно, причем обработка повторяется до тех пор, пока на профильтрованном изображении не прекратятся изменения. В другом варианте итеративного применения от шага к шагу итерации меняется апертура фильтра. В так называемом разделимом медианном фильтре одномерный медианный фильтр применяется сначала к каждой строке, а затем – к каждому столбцу изображения [34, стр. 183].
Разновидностью медианного фильтра является взвешенно-медианный фильтр [34, стр. 182]. В таком фильтре используется весовая функция, но интерпретируется она иначе, чем в линейных фильтрах. Здесь весовые коэффициенты показывают, сколько раз следует учитывать пиксели изображения, попавшие в апертуру.
Если выходу фильтра присваивать не значение медианы данных, находящихся в апертуре, а значение любой r -й (r = 1,2,... n, где n – общее число элементов апертуры) порядковой статистики, то можно получить n фильтров, названных процентильними [34, стр. 190]. Конечно, они, как обобщение медианного фильтра, также являются нелинейными. r -я порядковая статистика определяется как r -е по значению число из данных n чисел.
[1] В упрощенном варианте работы можно использовать встроенную в MathCAD функцию FFT для прямого и IFFT для обратного преобразований
[2] то же, что и примечание 1
* В первоисточнике использовано значение не A s2, а 1/ A s2.
Date: 2016-05-23; view: 5611; Нарушение авторских прав